Delone seti - Delone set
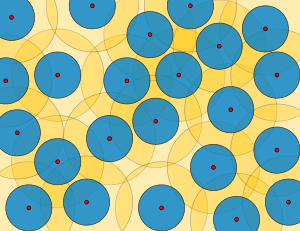
Matematiksel teorisinde metrik uzaylar, ε ağlar, ε-ambalajlar, ε kaplamalar, düzgün ayrık kümeler, nispeten yoğun kümeler, ve Delone setleri (adını Boris Delone ) iyi aralıklı nokta kümelerinin birbiriyle yakından ilişkili tanımları ve paketleme yarıçapı ve kaplama yarıçapı Bu setlerden hangisi ne kadar iyi aralıklı olduklarını ölçer. Bu setlerde uygulamalar var kodlama teorisi, yaklaşım algoritmaları ve teorisi yarı kristal.
Tanımlar
Eğer (M,d) bir metrik uzaydır ve X alt kümesidir M, sonra paketleme yarıçapı nın-nin X yarısı infimum farklı üyeleri arasındaki mesafelerin X. Salmastra yarıçapı ise r, sonra yarıçaplı topları açın r noktalarında ortalanmış X hepsi birbirinden ayrık olacak ve her açık top aşağıdaki noktalardan birinde ortalanacak X yarıçaplı 2r geri kalanından kopuk olacak X. kaplama yarıçapı nın-nin X sayıların sonsuzudur r öyle ki her noktası M mesafe içinde r en az bir puan X; yani en küçük yarıçaptır, öyle ki, bu yarıçaptaki kapalı toplar, X hepsine sahip M sendika olarak. Bir ε-paketleme bir set X paketleme yarıçapı ≥ε/ 2 (eşdeğer olarak, minimum mesafe ≥ ε), bir ε kaplama bir set X kaplama yarıçapı ≤ε, ve bir ε-net hem bir ε-paketleme ve bir ε- örtmek. Bir set düzgün ayrık sıfır olmayan bir paketleme yarıçapına sahipse ve nispeten yoğun sınırlı bir kaplama yarıçapına sahipse. Bir Delone seti hem tekbiçimli ayrı hem de nispeten yoğun bir kümedir; böylece, her ε-net Delone'dur, ancak tam tersi değildir.[1][2]
Ε-ağların yapımı
Yukarıdaki tanımların en kısıtlayıcı olanı olarak, y-ağları oluşturmak en azından y-dolgular, y-kaplamalar ve Delone setleri kadar zordur. Ancak, ne zaman noktaları M var iyi sipariş, sonsuz indüksiyon bir ε-net oluşturmanın mümkün olduğunu gösterir Ndahil ederek N sıralamadaki önceki noktalar kümesine olan uzaklıkların minimum olduğu her nokta en az ε. Sınırlı boyuta sahip bir Öklid uzayındaki sonlu nokta kümeleri için, her nokta, çapında bir hücre ızgarasına eşlenerek ve bir karma tablo hangi yakındaki hücrelerin zaten nokta içerdiğini test etmek için N; bu nedenle, bu durumda, bir ε-net inşa edilebilir doğrusal zaman.[3][4]
Daha genel sonlu veya kompakt metrik uzaylar, alternatif bir algoritma Teo Gonzalez göre en uzaktaki ilk geçiş sonlu bir ε-ağı oluşturmak için kullanılabilir. Bu algoritma ağı başlatır N boş bırakılır ve ardından tekrar tekrar eklenir N en uzak nokta M itibaren N, keyfi olarak bağları koparmak ve tüm noktalarM ε mesafesi içindeN.[5] İçinde sınırlı iki katına çıkan uzaylar Gonzalez algoritması O (n günlükn) en uzak ve en yakın mesafeleri arasında polinom oranına sahip nokta kümeleri için süre ve rasgele nokta kümeleri için aynı zaman sınırında yaklaşık olarak hesaplanır.[6]
Başvurular
Kodlama teorisi
Teorisinde hata düzeltme kodları, bir içeren metrik uzay blok kodu C sabit uzunluktaki dizelerden oluşur n, büyüklüğünde bir alfabeyi devraldı q (olarak düşünülebilir vektörler ), ile Hamming metriği. Bu alan şu şekilde gösterilir: . Bu metrik uzayın kaplama yarıçapı ve paketleme yarıçapı, kodun hataları düzeltme yeteneği ile ilgilidir.
Yaklaşık algoritmalar
Har-Peled ve Raichel (2013) tasarım için "ağ ve erik" adını verdikleri algoritmik bir paradigmayı tanımlayın yaklaşım algoritmaları bir dizi nokta üzerinde tanımlanan belirli geometrik optimizasyon problemleri için Öklid uzayları. Bu tür bir algoritma, aşağıdaki adımları gerçekleştirerek çalışır:
- Rastgele bir nokta seçin p belirlenen noktadan en yakın komşusunu bulun qve aradaki mesafeye ε ayarlayın p ve q.
- Ε'nin (yaklaşık olarak) optimal çözüm değerinden daha büyük veya daha küçük olup olmadığını test edin (çözülen belirli optimizasyon problemine özel bir teknik kullanarak)
- Daha büyükse, en yakın komşusu ε'den daha uzak olan noktaları girdiden kaldırın.
- Daha küçükse, bir ε-net oluşturun Nve girişten içinde olmayan noktaları kaldırın N.
Her iki durumda da, beklenen kalan puan sayısı sabit bir faktör kadar azalır, bu nedenle zamana test adımı hakimdir. Gösterdikleri gibi, bu paradigma, hızlı yaklaşım algoritmaları oluşturmak için kullanılabilir. k-merkezi kümeleme, medyan mesafeli bir çift nokta bulma ve birkaç ilgili problem.
Bir hiyerarşik ağ sistemi ağ ağacı, kullanılabilir sınırlı iki katına çıkan uzaylar inşa etmek iyi ayrılmış çift ayrışmalar, geometrik anahtarlar ve yaklaşık en yakın komşular.[6][7]
Kristalografi
İçindeki puanlar için Öklid uzayı, bir set X bir Meyer seti nispeten yoğunsa ve fark seti X − X tekdüze olarak ayrıktır. Eşdeğer olarak, X her ikisi de bir Meyer kümesidir X ve X − X Delone vardır. Meyer kümelerinin adı Yves Meyer, onları tanıtan (farklı ama eşdeğer bir tanımla harmonik analiz ) matematiksel bir model olarak yarı kristal. Nokta kümelerini içerirler kafesler, Penrose döşemeleri, ve Minkowski toplamları bu kümelerin sonlu kümeler ile.[8]
Voronoi hücreleri simetrik Delone setleri formu boşluk dolduran çokyüzlüler aranan Plesiohedra.[9]
Ayrıca bakınız
Referanslar
- ^ Clarkson, Kenneth L. (2006), "kullanarak üçgenleme oluşturma εağlar ", STOC'06: 38. Yıllık ACM Hesaplama Teorisi Sempozyumu Bildirileri, New York: ACM, s. 326–335, doi:10.1145/1132516.1132564, ISBN 1595931341, BAY 2277158.
- ^ Bazı kaynaklar "ε-net "burada an denilen şey için"ε-kaplama "; bkz., ör. Sutherland, W. A. (1975), Metrik ve topolojik uzaylara girişOxford University Press, s. 110, ISBN 0-19-853161-3, Zbl 0304.54002.
- ^ Har-Peled, S. (2004), "Kümeleme hareketi", Ayrık ve Hesaplamalı Geometri, 31 (4): 545–565, doi:10.1007 / s00454-004-2822-7, BAY 2053498.
- ^ Har-Peled, S .; Raichel, B. (2013), "Ağ ve erik: Öklid mesafe problemleri için doğrusal bir zaman algoritması", STOC'13: 45. Yıllık ACM Hesaplama Teorisi Sempozyumu Bildirileri, s. 605–614, arXiv:1409.7425.
- ^ Gonzalez, T. F. (1985), "Kümeler arası maksimum mesafeyi en aza indirmek için kümeleme", Teorik Bilgisayar Bilimleri, 38 (2–3): 293–306, doi:10.1016/0304-3975(85)90224-5, BAY 0807927.
- ^ a b Har-Peled, S .; Mendel, M. (2006), "Düşük boyutlu metriklerde ağların hızlı yapımı ve uygulamaları", Bilgi İşlem Üzerine SIAM Dergisi, 35 (5): 1148–1184, arXiv:cs / 0409057, doi:10.1137 / S0097539704446281, BAY 2217141.
- ^ Krauthgamer, Robert; Lee, James R. (2004), "Ağlarda gezinme: yakınlık araması için basit algoritmalar", 15. Yıllık ACM-SIAM Ayrık Algoritmalar Sempozyumu Bildirileri (SODA '04), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, s. 798–807, ISBN 0-89871-558-X.
- ^ Moody, Robert V. (1997), "Meyer setleri ve ikilileri", Uzun Menzilli Periyodik Düzenin Matematiği (Waterloo, ON, 1995), NATO İleri Bilim Enstitüleri C Serisi: Matematiksel ve Fiziksel Bilimler, 489, Dordrecht: Kluwer Academic Publishers, s. 403–441, BAY 1460032.
- ^ Grünbaum, Branko; Shephard, G.C. (1980), "Uyumlu çinilerle döşemeler", Amerikan Matematik Derneği Bülteni, Yeni seri, 3 (3): 951–973, doi:10.1090 / S0273-0979-1980-14827-2, BAY 0585178.
Dış bağlantılar
- Delone seti - Tilings Ansiklopedisi

