Yönlendirilmiş grafik - Directed graph

İçinde matematik ve daha spesifik olarak grafik teorisi, bir Yönlendirilmiş grafik (veya digraph) bir grafik bu bir dizi köşeler ile bağlanmıştır kenarlar, kenarların kendileriyle ilişkili bir yöne sahip olduğu yer.
Tanım
Biçimsel olarak, yönlendirilmiş bir grafik sıralı bir çifttir G = (V, Bir) nerede[1]
- V bir Ayarlamak kimin elementler arandı köşeler, düğümlerveya puan;
- Bir bir dizi sıralı çiftler köşe noktalarının adı oklar, yönlendirilmiş kenarlar (bazen basitçe kenarlar ilgili küme adı ile E onun yerine Bir), yönlendirilmiş yaylarveya yönlendirilmiş çizgiler.
Sıradan bir veya yönsüz grafik, ikincisi açısından tanımlandığı için sırasız çiftler genellikle adı verilen köşelerin kenarlar, yaylarveya çizgiler.
Yukarıda bahsedilen tanım, yönlendirilmiş bir grafiğin aynı kaynak ve hedef düğümlere sahip birden çok ok içermesine izin vermez, ancak bazı yazarlar, yönlendirilmiş grafiklerin bu tür çoklu oklara sahip olmasına izin veren daha geniş bir tanım düşünür (yani, okların bir çoklu set ). Daha spesifik olarak, bu varlıklar şu şekilde ele alınmaktadır: yönlendirilmiş multigraflar (veya çoklu grafik).
Öte yandan, yukarıda belirtilen tanım, yönlendirilmiş bir grafiğin döngüler (yani, düğümleri doğrudan kendilerine bağlayan oklar), ancak bazı yazarlar, yönlendirilmiş grafiklerin döngülere sahip olmasına izin vermeyen daha dar bir tanım düşünür.[2]Daha spesifik olarak, döngüleri olmayan yönlendirilmiş grafikler şu şekilde ele alınır: basit yönlendirilmiş grafiklerdöngüleri olan yönlendirilmiş grafikler şu şekilde ele alınmaktadır: döngü digraphs (bölüme bakın Yönlendirilmiş grafik türleri ).
Yönlendirilmiş grafik türleri
Alt sınıflar

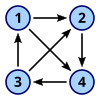
- Simetrik yönelimli grafikler tüm kenarların iki yönlü olduğu yönlendirilmiş grafiklerdir (yani digraph'a ait her ok için karşılık gelen ters ok da ona aittir).
- Basit yönlendirilmiş grafikler olmayan yönlendirilmiş grafiklerdir döngüler (köşeleri doğrudan kendilerine bağlayan oklar) ve aynı kaynak ve hedef düğümlere sahip birden fazla ok yok. Daha önce tanıtıldığı gibi, birden fazla ok olması durumunda varlık genellikle şu şekilde adreslenir: yönlendirilmiş multigraf. Bazı yazarlar döngüleri olan digrafları şöyle tanımlar: döngü digraphs.[2]
- Tam yönlendirilmiş grafikler her bir köşe çiftinin simetrik bir yönlendirilmiş ok çiftiyle birleştirildiği basit yönlendirilmiş grafiklerdir (yönsüz bir tam grafik kenarları ters ok çiftleriyle değiştirilir). Tam bir digrafın simetrik olduğu sonucu çıkar.
- Yönlendirilmiş grafikler çift yönlü kenarları olmayan yönlendirilmiş grafiklerdir (yani en fazla biri (x, y) ve (y, x) grafiğin okları olabilir). Bu, yönlendirilmiş bir grafiğin, ancak ve ancak herhangi bir 2 döngü.[3]
- Turnuvalar yönsüz olarak her kenar için bir yön seçerek elde edilen yönlendirilmiş grafiklerdir. tam grafikler.
- Yönlendirilmiş döngüsel olmayan grafikler (DAG'ler), hiçbir yönlendirilmiş döngüler.
- Çoklu ağaç tek bir başlangıç köşesinden gelen iki yönlendirilmiş yolun aynı bitiş noktasında geri gelmediği DAG'lerdir.
- Odaklı ağaçlar veya Polytrees Yönlendirilmemiş asiklik grafiklerin kenarlarının yönlendirilmesiyle oluşturulan DAG'lardır.
- Köklü ağaçlar alttaki yönsüz ağacın tüm kenarlarının kökten uzağa veya köke doğru yönlendirildiği yönlendirilmiş ağaçlardır.
Tamamlayıcı özelliklere sahip digraphs
- Ağırlıklı yönlendirilmiş grafikler (Ayrıca şöyle bilinir yönlendirilmiş ağlar) ile (basit) yönlendirilmiş grafiklerdir ağırlıklar oklarına atanmış, benzer şekilde ağırlıklı grafikler (aynı zamanda yönlendirilmemiş ağlar olarak da bilinir veya ağırlıklı ağlar ).[2]
- Akış ağları iki düğümün ayırt edildiği ağırlıklı yönlendirilmiş grafiklerdir, bir kaynak ve bir lavabo.
- Köklü yönlendirilmiş grafikler (Ayrıca şöyle bilinir akış grafikleri) bir tepe noktasının kök olarak ayırt edildiği digraflardır.
- Kontrol akış grafikleri bilgisayar biliminde, bir programın yürütülmesi sırasında geçilebilecek yolların bir temsili olarak kullanılan köklü digraflardır.
- Sinyal akış grafikleri düğümlerin sistem değişkenlerini ve dalların (kenarlar, yaylar veya oklar) düğüm çiftleri arasındaki fonksiyonel bağlantıları temsil ettiği yönlendirilmiş grafiklerdir.
- Akış grafikleri bir dizi doğrusal cebirsel veya diferansiyel denklemle ilişkili digraflardır.
- Durum diyagramları vardır yönlendirilmiş multigraflar temsil eden sonlu durum makineleri.
- Değişmeli diyagramlar kullanılan digraflar mı kategori teorisi, köşelerin (matematiksel) nesneleri temsil ettiği ve okların morfizmaları temsil ettiği, aynı başlangıç ve bitiş noktalarına sahip tüm yönlendirilmiş yolların kompozisyonla aynı sonuca yol açması özelliği ile.
- Teorisinde Lie grupları, bir titreme Q bir etki alanı olarak hizmet eden ve dolayısıyla şeklini karakterize eden yönlendirilmiş bir grafiktir. temsil V olarak tanımlanmış functor özellikle bir nesnesi functor kategorisi FinVctKF(Q) nerede F(Q) ücretsiz kategori açık Q yollardan oluşan Q ve FinVctK sonlu boyutlu kategorisidir vektör uzayları üzerinde alan K. Bir sadakın temsilleri, köşelerini vektör uzayları ve kenarları (ve dolayısıyla yolları) ile uyumlu olarak etiketler. doğrusal dönüşümler aralarında ve doğal dönüşümler.
Temel terminoloji
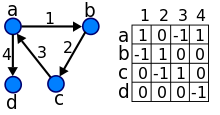
Bir ok (x, y) yönlendirildiği kabul edilir itibaren x -e y; y denir baş ve x denir kuyruk ok; y olduğu söyleniyor doğrudan halef nın-nin x ve x olduğu söyleniyor doğrudan selef nın-nin y. Eğer bir yol yol açar x -e y, sonra y olduğu söyleniyor halef nın-nin x ve ulaşılabilir itibaren x, ve x olduğu söyleniyor selef nın-nin y. Ok (y, x) denir ters ok nın-nin (x, y).
bitişik matris döngüleri olan bir multidigrafın tamsayı değerlidir matris köşelere karşılık gelen satırlar ve sütunlar ile, burada köşegen olmayan bir giriş aij tepe noktasından gelen okların sayısıdır ben tepe noktasına jve çapraz giriş aii tepe noktasındaki döngülerin sayısıdır ben. Yönlendirilmiş bir grafiğin bitişik matrisi, satırların ve sütunların aynı permütasyonuna kadar benzersizdir.
Yönlendirilmiş bir grafik için başka bir matris gösterimi, insidans matrisi.
Görmek yön daha fazla tanım için.
Dereceli ve aşırı derece

Bir tepe noktası için, bir tepe noktasına bitişik olan kafa uçlarının sayısına itiraz etmek tepe noktası ve bir tepe noktasına bitişik kuyruk uçlarının sayısı, üstünlük (aranan dallanma faktörü Ağaçlarda).
İzin Vermek G = (V, Bir) ve v ∈ V. İnkar edilemez v derece olarak gösterilir−(v) ve dış derecesi derece olarak gösterilir+(v).
Bir tepe noktası derece−(v) = 0 denir kaynak, çıkan oklarının her birinin kaynağı olduğu için. Benzer şekilde, bir tepe noktası derece+(v) = 0 denir lavabo, çünkü gelen oklarının her birinin sonu.
derece toplamı formülü yönlendirilmiş bir grafik için,
Her köşe için v ∈ V, derece+(v) = derece−(v)grafiğe a dengeli yönlü grafik.[4]
Derece sırası
Yönlendirilmiş bir grafiğin derece dizisi, belirsiz ve derece dışı çiftlerinin listesidir; yukarıdaki örnek için derece dizisine sahibiz ((2, 0), (2, 2), (0, 2), (1, 1)). Derece dizisi yönlendirilmiş bir grafik değişmezidir, bu nedenle izomorfik yönlendirilmiş grafikler aynı derece dizisine sahiptir. Bununla birlikte, derece dizisi genel olarak yönlendirilmiş bir grafiği benzersiz bir şekilde tanımlamaz; bazı durumlarda, izomorfik olmayan digraflar aynı derece dizisine sahiptir.
yönlendirilmiş grafik gerçekleştirme problemi belirli bir pozitif dizinin derece dizisi ile yönlendirilmiş bir grafik bulma problemidir tamsayı çiftler. (İzleyen sıfır çiftleri, yönlendirilmiş grafiğe uygun sayıda izole köşe eklenerek önemsiz bir şekilde gerçekleştirildikleri için göz ardı edilebilir.) Yönlendirilmiş bir grafiğin derece dizisi olan, yani yönlendirilmiş grafik gerçekleştirme probleminin bir çözümü olduğu bir dizi , yönlendirilmiş grafik veya yönlendirilmiş grafik dizisi olarak adlandırılır. Bu sorun ya şu şekilde çözülebilir: Kleitman – Wang algoritması veya tarafından Fulkerson-Chen-Anstee teoremi.
Yönlendirilmiş grafik bağlantısı
Yönlendirilmiş bir grafik zayıf bağlı (ya da sadece bağlı[5]) eğer yönlendirilmemişse temel grafik grafiğin tüm yönlendirilmiş kenarlarının yönsüz kenarlarla değiştirilmesiyle elde edilen bir bağlantılı grafik. Yönlendirilmiş bir grafik güçlü bir şekilde bağlı veya kuvvetli dan yönlendirilmiş bir yol içeriyorsa x -e y ve yönlendirilmiş bir yol y -e x her köşe çifti için {x, y}. güçlü bileşenler maksimum güçlü bir şekilde bağlı alt grafiklerdir.
Ayrıca bakınız
- Coates grafiği
- DRAKON akış şeması
- Akış şeması
- Grafik teorisi sözlüğü
- Grafik teorisi
- Grafik (soyut veri türü)
- Ağ teorisi
- Oryantasyon
- Ön sipariş
- Topolojik sıralama
- Grafiği transpoze et
- Dikey sınırlama grafiği
- Küresel set
Notlar
- ^ Bang-Jensen ve Gutin (2000). Diestel (2005) Bölüm 1.10. Bondy ve Murty (1976) Bölüm 10.
- ^ a b c Chartrand, Gary (1977). Giriş Grafiği Teorisi. Courier Corporation. ISBN 9780486247755.
- ^ Diestel (2005) Bölüm 1.10.
- ^ Satyanarayana, Bhavanari; Prasad, Kuncham Syam, Ayrık Matematik ve Grafik Teorisi, PHI Learning Pvt. Ltd., s. 460, ISBN 978-81-203-3842-5; Brualdi Richard A. (2006), Kombinatoryal Matris Sınıfları Matematik Ansiklopedisi ve Uygulamaları, 108, Cambridge University Press, s.51, ISBN 978-0-521-86565-4.
- ^ Bang-Jensen ve Gutin (2000) s. 2007 baskısında 19; s. 2. baskıda (2009) 20.
Referanslar
- Bang-Jensen, Jürgen; Gutin Gregory (2000), Digraphs: Teori, Algoritmalar ve Uygulamalar, Springer, ISBN 1-85233-268-9
(2007'nin düzeltilmiş 1. baskısı artık yazarların sitesinde ücretsiz olarak mevcuttur; 2. baskı 2009'da çıktı ISBN 1-84800-997-6). - Bondy, John Adrian; Murty, ABD R. (1976), Uygulamalı Grafik Teorisi, Kuzey-Hollanda, ISBN 0-444-19451-7.
- Diestel Reinhard (2005), Grafik teorisi (3. baskı), Springer, ISBN 3-540-26182-6 (elektronik 3. baskı yazarın sitesinde ücretsiz olarak mevcuttur).
- Harary, Frank; Norman, Robert Z .; Cartwright, Dorwin (1965), Yapısal Modeller: Yönlendirilmiş Grafikler Teorisine Giriş, New York: Wiley.
- Düğümlü yönlendirilmiş grafiklerin (veya yönlendirilmiş grafiklerin) sayısı itibaren Tam Sayı Dizilerinin Çevrimiçi Ansiklopedisi

