Maksimum alt dizi sorunu - Maximum subarray problem
İçinde bilgisayar Bilimi, maksimum toplam alt dizi problemi verilen tek boyutlu içinde en büyük toplamı olan bitişik bir alt dizi bulma görevidir. dizi A [1 ... n] sayı. Resmi olarak görev, endeksleri bulmaktır ve ile , öyle ki toplam
mümkün olduğu kadar büyük. (Sorunun bazı formülasyonları, boş alt dizinin de dikkate alınmasına izin verir; boş alt dizinin tüm değerlerinin toplamı sıfırdır.) A giriş dizisindeki her sayı pozitif, negatif veya sıfır olabilir.[1]
Örneğin, [−2, 1, −3, 4, −1, 2, 1, −5, 4] değerleri dizisi için en büyük toplamı olan bitişik alt dizi [4, −1, 2, 1] toplamı 6 ile.
Bu sorunun bazı özellikleri şunlardır:
- Dizi tüm negatif olmayan sayıları içeriyorsa, sorun önemsizdir; maksimum alt dizi tüm dizidir.
- Dizi pozitif olmayan tüm sayıları içeriyorsa, çözüm, dizinin (veya izin veriliyorsa boş alt dizinin) maksimum değerini içeren boyut 1'deki herhangi bir alt dizidir.
- Birkaç farklı alt dizinin aynı maksimum toplamı olabilir.
Bu problem, kaba kuvvet dahil olmak üzere birkaç farklı algoritmik teknik kullanılarak çözülebilir.[2] böl ve fethet,[3] dinamik program,[4] ve en kısa yollara indirgeme.[kaynak belirtilmeli ]
Tarih
Maksimum alt dizi problemi tarafından önerildi Ulf Grenander 1977'de basitleştirilmiş bir model olarak maksimum olasılık sayısallaştırılmış görüntülerde örüntü tahmini.[5]
Grenander, iki boyutlu bir gerçek sayı dizisi içinde, maksimum toplamı olan dikdörtgen bir alt dizi bulmaya çalışıyordu. İki boyutlu problem için kaba kuvvet algoritması çalışır. Ö(n6) zaman; Bu engelleyici bir şekilde yavaş olduğu için, Grenander tek boyutlu problemi yapısını anlamak için önerdi. Grenander, tek boyutlu problemi çözen bir algoritma türetmiştir. Ö(n2) zaman,[not 1]kaba kuvvet çalışma süresinin iyileştirilmesi Ö(n3). Ne zaman Michael Shamos sorunu duydu, bir gecede bir Ö(n günlük n) böl ve yönet algoritması Kısa süre sonra Shamos tek boyutlu sorunu ve geçmişini bir Carnegie Mellon Üniversitesi katıldığı seminer Jay Kadane, bir dakika içinde tasarlayan Ö(n) -zaman algoritması,[5][6][7] mümkün olduğu kadar hızlı.[not 2] 1982'de David Gries aynısını elde etti Ö(n) -zaman algoritması uygulayarak Dijkstra "standart stratejisi";[8] 1989'da, Richard Bird bunu kullanarak kaba kuvvet algoritmasının tamamen cebirsel manipülasyonu ile türetilmiştir. Kuş-Meertens biçimciliği.[9]
Grenander'ın iki boyutlu genellemesi O (n3) Kadane algoritmasını bir alt yordam olarak kullanarak veya bir böl ve yönet yaklaşımı aracılığıyla zaman. Biraz daha hızlı algoritmalar uzaklık matrisi çarpımı tarafından önerildi Tamaki ve Tokuyama (1998) ve tarafından Takaoka (2002). Önemli ölçüde daha hızlı bir algoritmanın bulunmadığına dair bazı kanıtlar vardır; O'daki iki boyutlu maksimum alt dizi problemini çözen bir algoritma (n3 − ε) herhangi bir ε> 0 için zaman, benzer şekilde hızlı bir algoritma anlamına gelir. tüm çiftler en kısa yollar sorun.[10]
Başvurular
Bu bölüm Hesaplamalı biyoloji uzmanının ilgilenmesi gerekiyor. Spesifik sorun şudur: satır içi etiketleri düzeltin. (Eylül 2019) |
Maksimum alt dizi problemleri, genomik gibi birçok alanda ortaya çıkar dizi analizi ve Bilgisayar görüşü.
Genomik dizi analizi, protein dizilerinin önemli biyolojik bölümlerini tanımlamak için maksimum alt dizi algoritmalarını kullanır.[kaynak belirtilmeli ] Bu sorunlar, korunmuş segmentleri, GC açısından zengin bölgeleri, ardışık tekrarları, düşük karmaşıklık filtresini, DNA bağlanma alanlarını ve yüksek yüklü bölgeleri içerir.[kaynak belirtilmeli ]
İçinde Bilgisayar görüşü, maksimum alt dizi algoritmaları, bir görüntüdeki en parlak alanı algılamak için bitmap görüntülerde kullanılır.
Kadane algoritması
| Örnek çalışma |
|---|
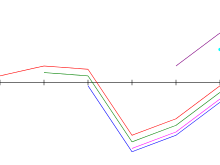
 Kadane algoritmasının yukarıda örnek dizi. Mavi: en büyük toplamı ile biten alt dizi ben; yeşil: şimdiye kadar karşılaşılan en büyük toplamlı alt dizi; küçük harf, boş bir diziyi belirtir; değişken ben Python kodunda örtük bırakılır. |
Kadane's algoritma verilen diziyi tarar soldan sağa. İçinde Adımda, en büyük toplamı biten alt diziyi hesaplar. ; bu toplam değişken olarak tutulur geçerli_toplam.[not 3]Dahası, alt diziyi herhangi bir yerde en büyük toplamı ile hesaplar. , değişkende tutulur best_sum,[not 4]ve tüm değerlerin maksimumu olarak kolayca elde edilir geçerli_toplam şimdiye kadar görüldü, cf. algoritmanın 7. satırı.
Olarak döngüsel değişmez, içinde adım, eski değeri geçerli_toplam her yerde maksimum tutar toplamın .[not 5]Bu nedenle, geçerli_toplam[not 6]her şeyden önce maksimumdur toplamın . Davayı da kapsayacak şekilde ikinci maksimumu genişletmek için boş alt diziyi de düşünmek yeterlidir . Bu 6. satırda atanarak yapılır geçerli_toplam yeni değeri olarak geçerli_toplam, bundan sonra maksimum tutar toplamın .
Böylelikle aşağıdaki kod ile sorun çözülebilir,[4][7] burada ifade Python:
1 def max_subarray(sayılar):2 "" "Herhangi bir bitişik alt dizinin en büyük toplamını bulun." ""3 best_sum = 0 # veya: float ('- inf')4 geçerli_toplam = 05 için x içinde sayılar:6 geçerli_toplam = max(0, geçerli_toplam + x)7 best_sum = max(best_sum, geçerli_toplam)8 dönüş best_sumAlgoritmanın bu sürümü, girdi pozitif öğe içermiyorsa (girişin boş olduğu durumlar dahil) 0 döndürür. Sorunun boş alt dizilere izin vermeyen varyantı için, best_sum bunun yerine negatif sonsuza başlatılmalıdır[11] ve ayrıca for döngüsünde geçerli_toplam olarak güncellenmeli maks (x, cari_sum + x).[not 7]Bu durumda, giriş pozitif öğe içermiyorsa, döndürülen değer en büyük öğenin değeridir (yani, en az negatif değer) veya giriş boşsa negatif sonsuzdur.
Algoritma, maksimum alt dizinin başlangıç ve bitiş endekslerini de takip etmek için değiştirilebilir:
1 def max_subarray(sayılar): 2 "" "En büyük toplamı olan bitişik bir alt dizi bulun." "" 3 best_sum = 0 # veya: float ('- inf') 4 best_start = best_end = 0 # veya: Yok 5 geçerli_toplam = 0 6 için current_end, x içinde numaralandırmak(sayılar): 7 Eğer geçerli_toplam <= 0: 8 # Mevcut öğede yeni bir sıra başlatın 9 current_start = current_end10 geçerli_toplam = x11 Başka:12 # Mevcut sırayı mevcut elemanla genişlet13 geçerli_toplam += x14 15 Eğer geçerli_toplam > best_sum:16 best_sum = geçerli_toplam17 best_start = current_start18 best_end = current_end + 1 # +1 "en iyi_sonu" özel kılmaktır19 20 dönüş best_sum, best_start, best_endPython'da, diziler 0'dan başlayarak dizinlenir ve bitiş dizini tipik olarak hariç tutulur, böylece [-11, 22, 33, -44] dizisindeki alt dizi [22, 33] dizin 1'de başlar ve dizinde biter 3.
Bu algoritmanın optimal alt yapıları kullanma şekli nedeniyle (her bir konumda sonlanan maksimum alt dizi, ilgili ancak daha küçük ve örtüşen bir alt problemden basit bir şekilde hesaplanır: önceki konumda biten maksimum alt dizi), bu algoritma basit / basit olarak görülebilir. önemsiz örneği dinamik program.
Kadane algoritmasının çalışma zamanı karmaşıklığı .[4][7]
Genellemeler
Daha yüksek boyutlu diziler için benzer sorunlar ortaya çıkabilir, ancak bunların çözümleri daha karmaşıktır; örneğin bkz. Takaoka (2002). Brodal ve Jørgensen (2007) nasıl bulunacağını gösterdi k tek boyutlu bir dizideki en büyük alt dizi toplamları, optimum zaman sınırında .
Maksimum toplam k-disjoint alt dizileri de optimum zaman sınırında hesaplanabilir .[12]
Ayrıca bakınız
Notlar
- ^ Önceden hesaplanmış kümülatif toplamlar tablosu kullanarak alt dizi toplamını hesaplamak için sabit zamanda
- ^ çünkü her algoritma, en azından bir kez alan diziyi taramalıdır. Ö(n) zaman
- ^ isimli
MaxEndingHereiçinde Bentley (1989), veciçinde Gries (1982) - ^ isimli
MaxSoFariçinde Bentley (1989), vesiçinde Gries (1982) - ^ Bu meblağ ne zaman , boş alt diziye karşılık gelir .
- ^ Python kodunda, olarak ifade edilir
x, indeks ile örtük bırakıldı. - ^ İkinci değişiklikten bahsedilmemekle birlikte Bentley (1989), değiştirilmiş döngü değişmezliğini korumayı başarır
geçerli_toplambaşlangıcında inci adım.
Referanslar
- ^ Bentley 1989, s. 69.
- ^ Bentley 1989, s. 70.
- ^ Bentley 1989, s. 73.
- ^ a b c Bentley 1989, s. 74.
- ^ a b Bentley 1984, s. 868-869.
- ^ Bentley 1989, s. 76-77.
- ^ a b c Gries 1982, s. 211.
- ^ Gries 1982, s. 209-211.
- ^ Kuş 1989, Bölüm 8, s. 126.
- ^ Backurs, Dikkala ve Tzamos 2016.
- ^ Bentley 1989, s. 78,171.
- ^ Bengtsson ve Chen 2007.
- Backurs, Arturs; Dikkala, Nişant; Tzamos, Christos (2016), "Maksimum Ağırlıklı Dikdörtgenler için Sıkı Sertlik Sonuçları", Proc. Otomata, Diller ve Programlama Konulu 43. Uluslararası Kolokyum: 81:1–81:13, doi:10.4230 / LIPIcs.ICALP.2016.81, S2CID 12720136
- Bae, Sung Eun (2007), Genelleştirilmiş Maksimum Alt Dizi Problemi için Sıralı ve Paralel Algoritmalar (PDF) (Doktora tezi), Canterbury Üniversitesi, S2CID 2681670.
- Bengtsson, Fredrik; Chen, Jingsen (2007), Maksimum puan alan segmentleri en iyi şekilde hesaplama (PDF) (Araştırma raporu), Luleå Teknoloji Üniversitesi
- Bentley, Jon (1984), "Programlama İncileri: Algoritma Tasarım Teknikleri", ACM'nin iletişimi, 27 (9): 865–873, doi:10.1145/358234.381162, S2CID 207565329
- Bentley, Jon (Mayıs 1989), İncileri Programlama (2. baskı), Reading, MA: Addison Wesley, ISBN 0-201-10331-1
- Kuş, Richard S. (1989), "Program Hesaplaması için Cebirsel Kimlikler" (PDF), Bilgisayar Dergisi, 32 (2): 122–126, doi:10.1093 / comjnl / 32.2.122
- Brodal, Gerth Stølting; Jørgensen, Allan Grønlund (2007), "Bir doğrusal zaman algoritması k maksimum toplamlar sorunu ", Bilgisayar Biliminin Matematiksel Temelleri, Bilgisayar Bilimleri Ders Notları, 4708, Springer-Verlag, s. 442–453, doi:10.1007/978-3-540-74456-6_40.
- Gries, David (1982), "Döngü Değişkenleri ve Döngüleri Geliştirmek İçin Standart Stratejiye İlişkin Bir Not" (PDF), Bilgisayar Programlama Bilimi, 2 (3): 207–241, doi:10.1016/0167-6423(83)90015-1, hdl:1813/6370
- Takaoka, Tadao (2002), "Mesafe matrisi çarpımı ile maksimum alt dizi problemi için verimli algoritmalar", Teorik Bilgisayar Bilimlerinde Elektronik Notlar, 61: 191–200, doi:10.1016 / S1571-0661 (04) 00313-5.
- Tamaki, Hisao; Tokuyama, Takeshi (1998), "Matris Çarpımına Dayalı Maksimum Alt Dizi Problemi için Algoritmalar", 9. Ayrık Algoritmalar Sempozyumu (SODA) Bildirileri: 446–452, alındı 17 Kasım 2018
Dış bağlantılar
- TAN, Lirong. "Maksimum Bitişik Alt Dizi Toplamı Sorunları" (PDF). Arşivlenen orijinal (PDF) 2015-10-10 tarihinde. Alındı 2017-10-26.
- Mu, Shin-Cheng (2010). "Maksimum Segment Toplamı Problemi: Kökeni ve Türetme".
- "Maksimum Alt Dizi Problemi Üzerine Notlar". 2012.
- www.algorithmist.com
- alexeigor.wikidot.com
- Rosetta Kodundaki en büyük ardışık toplam problemi
- Kadane Algoritması ile ilgili geeksforgeeks sayfası




![{displaystyle toplamı _ {x = i} ^ {j} A [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f4ae4590a685044ab6ba7cc8b23cc7c57f5689e)
![{displaystyle A [1ldots n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3d1923568ccfdc916c6cd1c84cb282a32af9074)
![{displaystyle A [1ldots j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f81bf04402d996fbf9efe4c9e68c68d804022adf)

![{displaystyle A [i] + cdots + A [j-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d953b5c43fc85b567297a449586a6aa761a6c83)
![{displaystyle + A [j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f276f74cd74ae67e23c51b1e9ef3764c5798adfd)
![{displaystyle A [i] + cdots + A [j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce9a7a1d7259eb0056fc37f9bed9219049cb8cde)

![{displaystyle A [j + 1; ldots; j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7cbec3c9700cbffc27f7452cc996629800229e)

![{displaystyle + A [j])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/188c430a18abd0a38d9b527d13d3abd631d0d51e)



![{displaystyle S [k] = toplam _ {x = 1} ^ {k} A [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec8da87a55750ee8f1489589facd90c9bb8bfee)
![{displaystyle toplamı _ {x = i} ^ {j} A [x] = S [j] -S [i-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5eaeb881301c21c223bcda980954ff927f9f6b9)


![{displaystyle A [jldots j-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aacd5b052234fec25693efb7c84dd6839025a9fc)
![{displaystyle A [j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c385fd9b0f771529e587f216f3f15d52bb85ef6)
![{displaystyle = max _ {iin {1, ..., j}} A [i] + ... + A [j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ecd64c15844772c73f9c1a76a75ceed97b6e58a)