Ağaç kapsayan minimum darboğaz - Minimum bottleneck spanning tree
Matematikte bir minimum darboğaz kapsayan ağaç (MBST) yönsüz bir grafikte yayılan ağaç en pahalı kenarın mümkün olduğu kadar ucuz olduğu. Darboğaz kenarı, kapsayan bir ağaçtaki en yüksek ağırlıklı kenardır. Bir kapsayan ağaç, grafik daha küçük bir darboğaz kenar ağırlığına sahip bir kapsayan ağaç içermiyorsa, ağacı kapsayan minimum bir darboğazdır.[1] Yönlendirilmiş bir grafik için benzer bir sorun olarak bilinir Minimum Darboğaz Yayılan Arborescence (MBSA).
Tanımlar
Yönsüz grafikler

Yönsüz bir grafikte G(V, E) ve bir işlev w : E → R, İzin Vermek S tüm yayılan ağaçların kümesi ol Tben. İzin Vermek B(Tben) herhangi bir kapsayan ağaç için maksimum ağırlık kenarı Tben. Ağaçları kapsayan minimum darboğaz alt kümesini tanımlıyoruz S′ Öyle ki herkes için Tj ∈ S′ ve Tk ∈ S sahibiz B(Tj) ≤ B(Tk) hepsi için ben vek.[2]
Sağdaki grafik bir MBST örneğidir, grafikteki kırmızı kenarlar bir MBST oluşturur. G(V, E).
Yönlendirilmiş grafikler

Bir grafik çardağı G yönlendirilmiş bir ağaçtır G belirli bir düğümden yönlendirilmiş bir yol içeren L bir alt kümenin her bir düğümüne V' nın-nin V \{L}. Düğüm L arboresansın kökü denir. Ağaçlanma, genişleyen bir çardaktır, eğer V′ = V \{L}. Bu durumda MBST, minimum darboğaz kenarı ile genişleyen bir çardaktır. Bu durumda bir MBST, Minimum Darboğaz Yayılan Arboresan (MBSA) olarak adlandırılır.
Sağdaki grafik bir MBSA örneğidir, grafikteki kırmızı kenarlar bir MBSA oluşturur. G(V, E).
Özellikleri
A MST (veya az yer kaplayan ağaç ) zorunlu olarak bir MBST'dir, ancak bir MBST mutlaka bir MST değildir.[3]
Yönlendirilmemiş grafikler için Camerini algoritması
Camerini önerdi[5] bir algoritma belirli bir yönlendirilmemiş, bağlı olarak asgari bir darboğaz kapsayan ağaç (MBST) elde etmek için kullanılır, kenar ağırlıklı grafik 1978'de. Kenarları ikiye böler. Bir setteki kenarların ağırlıkları diğerinden fazla değildir. Eğer bir yayılan ağaç Yalnızca daha küçük kenar kümesindeki kenarlarla oluşturulan alt grafikte bulunur, daha sonra alt grafikte bir MBST hesaplar, alt grafiğin MBST'si tam olarak orijinal grafiğin bir MBST'sidir. Eğer bir yayılan ağaç mevcut olmadığında, bağlantısı kesilen her bileşeni yeni bir süper köşede birleştirir ve daha sonra bu süper köşeler ve daha büyük kenar kümesindeki kenarlar tarafından oluşturulan grafikte bir MBST hesaplar. Bağlantısı kesilen her bileşendeki bir orman, orijinal grafikte bir MBST'nin parçasıdır. Grafikte iki (süper) köşe kalana ve aralarına en küçük ağırlıkta tek bir kenar eklenene kadar bu işlemi tekrarlayın. Önceki adımlarda bulunan tüm kenarlardan oluşan bir MBST bulunur.[4]
Sözde kod
Prosedürün iki giriş parametresi vardır. G bir grafiktir w grafikteki tüm kenarların ağırlık dizisidir G.[6]
1 işlevi MBST (grafik G, ağırlıklar w) 2 E ← kenar dizisi G 3 Eğer | E | = 1 sonra dönüş E Başka 4 Bir ← yarım kenarlar E ağırlıkları ortalama ağırlık 5'ten az olmayan B ← E - Bir 6 F ← orman GB 7 Eğer F yayılan bir ağaç sonra 8 dönüş MBST (GB,w) 9 Başka 10 dönüş MBST ((GBir)η, w) FYukarıda (GBir)η süper köşelerden (bağlantısı kesilmiş bir bileşendeki köşeleri tek olarak kabul ederek) ve içindeki kenarlardan oluşan alt grafiktir. Bir.
Çalışma süresi
Algoritma çalışıyor Ö (E) zaman, nerede E kenarların sayısıdır. Bu sınır şu şekilde elde edilir:
- medyan bulma algoritmalarıyla iki gruba ayrılıyor Ö(E)
- içinde orman bulmak Ö(E)
- her yinelemede E'deki yarım kenarlar dikkate alınarak Ö(E + E/2 + E/4 + ··· + 1) = Ö(E)
Misal
Aşağıdaki örnekte, bir MBST oluşturmak için yeşil kenarlar kullanılmıştır ve kesikli kırmızı alanlar, algoritma adımları sırasında oluşan süper köşeleri göstermektedir.
 | Algoritma yarım ağırlıklara göre kenarları iki küme böler. Yeşil kenarlar, ağırlıkları olabildiğince küçük olan kenarlardır. |
 | Alt grafikte sadece daha küçük kenarlarda kenarlarla oluşturulan bir yayılan ağaç olduğundan. Bu alt grafikte bir MBST bulmayı tekrarlayın. |
 | Mevcut alt grafikte, mevcut küçük kenar kümesinde kenarlarla oluşturulan bir kapsayan ağaç olmadığından. Bağlantısı kesilmiş bir bileşenin köşelerini bir süper tepe noktasıyla (kesikli kırmızı bir alanla gösterilir) birleştirin ve ardından daha büyük kenar kümesindeki süper köşeler ve kenarlarla oluşturulan alt grafikte bir MBST bulun. Bağlantısı kesilen her bileşenin içinde oluşan bir orman, orijinal grafikte bir MBST'nin parçası olacaktır. |
 | Daha fazla köşeyi bir süper tepe noktasına birleştirerek benzer adımları tekrarlayın. |
 | Algoritma sonunda, algoritma sırasında bulduğu kenarları kullanarak bir MBST elde eder. |
Yönlendirilmiş grafikler için MBSA algoritmaları
Yönlendirilmiş grafik için kullanılabilen iki algoritma vardır: Camerini'nin MBSA'yı bulmak için algoritması ve diğeri Gabow ve Tarjan'dan.[4]
Camerini'nin MBSA algoritması
Yönlendirilmiş bir grafik için, Camerini'nin algoritması, MBSA'nın darboğaz maliyeti olarak maksimum maliyetine sahip olacak kenar kümelerini bulmaya odaklanır. Bu, kenar kümesini bölümlere ayırarak yapılır. E iki set halinde Bir ve B ve seti korumak T bu, bilindiği settir GT genişleyen bir ağaçlandırma yok, artan T tarafından B ne zaman azami güçlense G(B ∪ T) genişleyen bir çardak değil Gyoksa azalırız E tarafındanBir. Toplam zaman karmaşıklığı Ö(E günlükE).[5][4]
Sözde kod
işlevi MBSA (G, w, T) dır-dir E ← kenar dizisi G Eğer | E - T | > 1 sonra Bir ← UH (E-T) B ← (E - T) − Bir F ← BURÇ (GFAKAT) Eğer F G'nin yayılan bir çardağıdır sonra S ← F MBSA ((GFAKAT), w, T) Başka MBSA (G, w, KÜVET);
- T, E'nin bir alt kümesini temsil eder, bunun için GT "a" düğümünde köklenen herhangi bir yayılma arboresansı içermez. Başlangıçta T boştur
- UH, G'deki (E − T) kenar setini alır ve aşağıdaki şekilde A ⊂ (E − T) döndürür:
- Wa ≥ Wb , a ∈ A ve b ∈ B için
- BUSH (G), kök "a" düğümünde bulunan G'nin maksimal arboresansını döndürür
- Nihai sonuç S olacak
Misal
   | Bu algoritmanın ilk yinelemesini çalıştırdıktan sonra, F ve F yayılan bir çardak değil GYani kodu çalıştırıyoruz |
   | İkinci yinelemede, ve aynı zamanda genişleyen bir çardak değil GYani kodu çalıştırıyoruz |
   | Üçüncü yinelemede, ve yayılan bir çardaktır GYani kodu çalıştırıyoruz |
  | koştuğumuzda , 1'den büyük olmayan 1'e eşittir, dolayısıyla algoritma geri döner ve nihai sonuç . |
MBSA için Gabow ve Tarjan algoritması
Gabow ve Tarjan, Dijkstra algoritması MBSA üreten tek kaynaklı en kısa yol için. Algoritmaları çalışıyor Ö(E + V günlükV) zaman eğer Fibonacci yığını Kullanılmış.[7]
Sözde kod
Bir grafik için G (V, E), F köşelerin bir koleksiyonudur V. Başlangıçta, F = {s} nerede s grafiğin başlangıç noktasıdır G ve c(s) = -∞ 1 işlevi MBSA-GT (G, w, T) 2 tekrar et | V | kez 3 seçin v minimum ile c(v) itibaren F; 4 F; 5 için ∀ kenar (v, w) yapmak 6 Eğer w ∉ F veya ∉ Ağaç sonra 7 ekle w -e F; 8 c(w) = c(v, w); 9 p(w) = v; 10 Başka 11 Eğer w ∈ F ve c (w)> c (v, w) sonra 12 c(w) = c(v, w); 13 p(w) = v;Misal
Aşağıdaki örnek, algoritmanın nasıl çalıştığını göstermektedir.
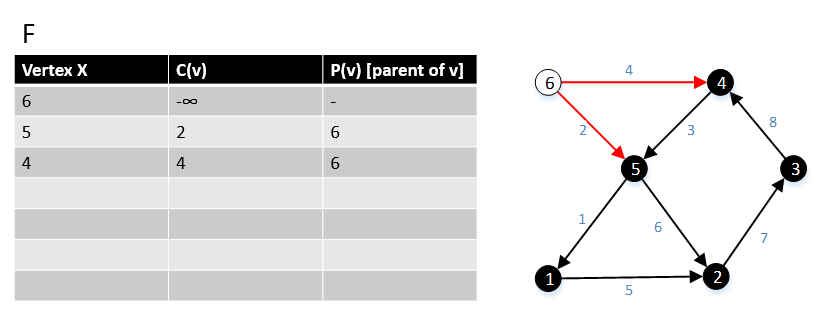 Algoritmanın ilk adımında G grafiğinden s kökünü seçiyoruz, yukarıdaki şekilde köşe 6, kök s'dir. Sonra tüm kenarları (6, w) ∈ E ve maliyetlerini c (6, w) bulduk, burada w ∈ V. |
 Daha sonra G grafiğinde tepe noktası 5'e gidiyoruz, tüm kenarları (5, w) E ve maliyetlerini c (5, w) bulduk, burada w ∈ V. |
 Daha sonra G grafiğinde tepe 4'e gidiyoruz, tüm (4, w) ∈ E kenarlarını ve bunların maliyetini c (4, w) bulduk, burada w ∈ V. Kenarın (4,5)> kenar (6.5), böylece kenarı (6,5) tutup kenarı (4,5) kaldırıyoruz. |
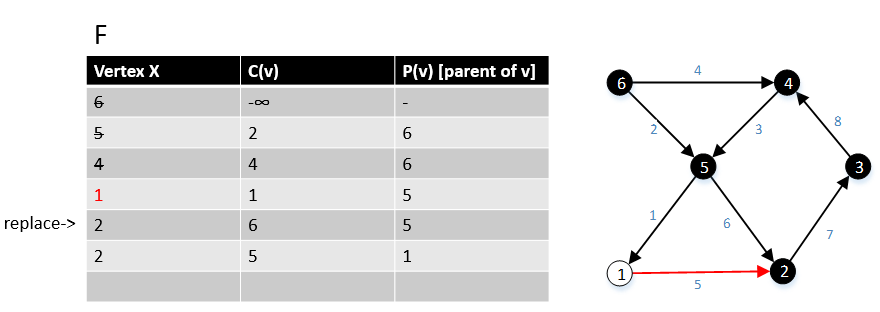 Sonra G grafiğinde tepe noktası 1'e gidiyoruz, tüm (1, w) ∈ E kenarlarını ve bunların maliyetini c (1, w) bulduk, burada w ∈ V. Kenarın (5,2)> kenar (1,2), bu yüzden kenarı (5,2) kaldırıp kenarı (1,2) tutuyoruz. |
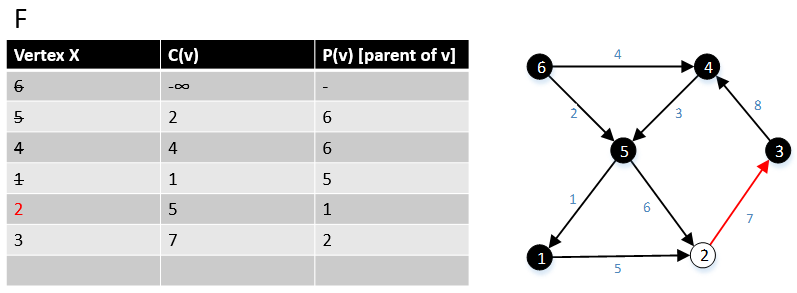 Daha sonra G grafiğinde tepe 2'ye gidiyoruz, tüm (2, w) ∈ E kenarlarını ve bunların maliyetini c (2, w) bulduk, burada w ∈ V. |
 Daha sonra, G grafiğinde tepe 3'e gidiyoruz, tüm (3, w) ∈ E kenarlarını ve bunların maliyetini c (3, w) bulduk, burada w ∈ V. Kenarın (3,4)> kenar (6,4), bu yüzden kenarı (3,4) kaldırıp kenarı (6,4) tutuyoruz. |
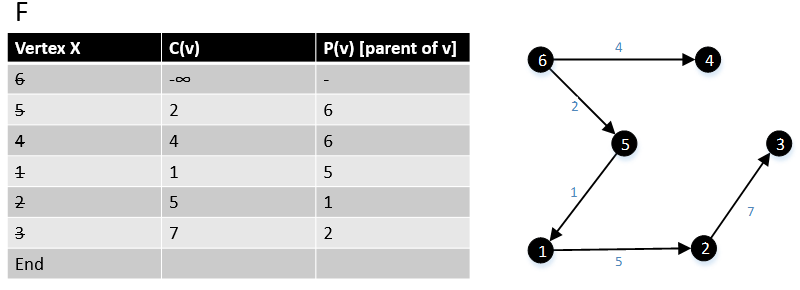 G grafiğindeki tüm köşelerden geçtikten sonra algoritma bitmiştir. |
Tarjan ve Gabow tarafından önerilen bir başka yaklaşım Ö(E günlük* V) Camerini’nin MBSA algoritmasına çok benzeyen seyrek grafikler için, ancak kenar kümesini her yineleme başına iki kümeye bölmek yerine, K(ben) hangi ben gerçekleşen bölünmelerin sayısı veya başka bir deyişle yineleme sayısıdır ve K(ben) yineleme başına sahip olması gereken bölümlenmiş kümelerin sayısını gösteren artan bir işlevdir. K(ben) = 2k(ben − 1) ile k(1) = 2. Algoritma bulur λ* herhangi bir MBSA'daki darboğaz kenarının değeridir. Sonra λ* içinde herhangi bir arborescence bulundu G(λ*) bir MBSA'dır. G(λ*) tüm kenar maliyetlerinin olduğu grafiktir ≤ λ*.[4][7]
Referanslar
- ^ Darboğaz Yayılan Ağaç hakkında her şey
- ^ Murali, T.M. (2009), Minimum Yayılma Ağaçlarının Uygulamaları (PDF)
- ^ 3. soruda bu iddia için bir kanıtınız var (PDF)
- ^ a b c d e Traboulsi, Ahmad (2014), Ağaçları Kapsayan Darboğaz (PDF), dan arşivlendi orijinal (PDF) 2016-03-04 tarihinde, alındı 2014-12-28
- ^ a b Camerini, P.M. (1978), "Min-max yayılma ağacı sorunu ve bazı uzantılar", Bilgi İşlem Mektupları, 7 (1): 10, doi:10.1016/0020-0190(78)90030-3
- ^ Cui, Yuxiang (2013), Minimum Darboğaz Kapsama Ağacı (PDF), dan arşivlendi orijinal (PDF) 2016-03-04 tarihinde, alındı 2014-12-28
- ^ a b Gabow, Harold N; Tarjan, Robert E (1988). "İki darboğaz optimizasyon problemi için algoritmalar". Algoritmalar Dergisi. 9 (3): 411–417. doi:10.1016/0196-6774(88)90031-4. ISSN 0196-6774.










