Üçgenlerin benzerlik sistemi - Similarity system of triangles
Bir üçgenlerin benzerlik sistemi bir dizi üçgeni içeren özel bir konfigürasyondur.[1] Bir dizi üçgen bir konfigürasyon tüm üçgenler kümede bulunan diğer üçgenlerden biriyle minimum bir olay ilişkisini paylaştığında.[1] Bir insidans ilişkisi üçgenler arasında, iki üçgenin bir noktayı paylaşması anlamına gelir. Örneğin, sağdaki iki üçgen, ve iki olay ilişkisinden oluşan bir konfigürasyondur, çünkü ve paylaşılır. Konfigürasyonları oluşturan üçgenler, bileşen üçgenler olarak bilinir.[1] Üçgenler, bir benzerlik sisteminde olmak için sadece bir konfigürasyon setinin parçası olmamalı, aynı zamanda doğrudan benzer olmalıdır.[1] Doğrudan benzerlik, tüm açıların verilen iki üçgen arasında eşit olduğunu ve aynı dönme hissini paylaştıkları anlamına gelir.[2] Bitişik görüntülerde görüldüğü gibi, doğrudan benzer üçgenlerde, üstüne ve üstüne aynı yönde meydana gelir. Karşıt benzer üçgenlerde, döndürme üstüne ve üstüne ters yönde meydana gelir. Özetle, bir konfigürasyon, kümedeki tüm üçgenlerin aynı düzlemde olduğu ve aşağıdakilerin geçerli olduğu bir benzerlik sistemidir: n setteki üçgenler ve n - 1 üçgen doğrudan benzerdir, daha sonra n üçgen doğrudan benzerdir.[1]
Arka fon
J.G. Mauldon, üçgenlerin benzerlik sistemleri fikrini makalesinde tanıttı. Matematik Dergisi "Benzer Üçgenler".[1] Mauldon analizlerine verilen üçgenleri inceleyerek başladı karmaşık sayılarla doğrudan benzerlik için, özellikle denklem .[1] Daha sonra analizlerini eşkenar üçgenlere doğru genişletti ve eğer bir üçgen denklemi tatmin etmek ne zaman , eşkenardı.[1] Bu çalışmanın kanıtı olarak, doğrudan benzerlik ve eşkenar üçgenler hakkındaki varsayımlarını Napolyon teoremi.[1] Daha sonra Napolyon'u, her bir tepe noktasına denk gelen eşkenar üçgenlerle bir eşkenar üçgen oluşturulmuşsa, dıştaki üç eşkenar üçgenin gelişmeyen köşeleri arasındaki bağlantı çizgilerinin orta noktalarının bir eşkenar üçgen oluşturduğunu kanıtlayarak Napolyon'u inşa etti.[1] Diğer benzer çalışmalar Fransız Geometer tarafından yapıldı Thébault Paralelkenar ve paralelkenarın her iki yanında yer alan kareler verildiğinde, karelerin merkezleri bir kare oluşturur.[3] Mauldon daha sonra eş düzlemli üçgen kümelerini analiz ederek, kriterlere dayalı benzerlik sistemleri olup olmadıklarını belirledi, eğer üçgenlerden biri hariç hepsi doğrudan benzer ise, o zaman tüm üçgenler doğrudan benzerdir.[1]
Örnekler
Dikdörtgene eklenen üçgenler
Doğrudan benzerlik
Bir dikdörtgen oluşturursak doğrudan benzer üçgenlerle dikdörtgenin her iki yanında , sonra doğrudan benzer ve üçgenler kümesi bir benzerlik sistemidir.[1]
Dolaylı benzerlik
Bununla birlikte, üçgenlerin dejenere olabileceğini ve puan alabileceğini kabul edersek ve birbirlerine yalan söylemek ve Birbirlerinin üzerine uzandıklarında, üçgen kümesi artık doğrudan bir benzerlik sistemi değildir, çünkü ikinci üçgenin alanı vardır ve diğerleri yoktur.[1]
Dikdörtgen paralel yüzlü
Üç çizgi dizisinin paralel olduğu, ancak uzunluklarının eşdeğer olmadığı bir şekil verildiğinde (resmi olarak dikdörtgen olarak bilinir) paralel yüzlü ) ikinci sıradaki tüm noktalar aşağıdaki gibi etiketlenmiştir:
Sonra yukarıdaki noktaları alıp üçgen olarak analiz edebilir ve bir benzerlik sistemi oluşturduklarını gösterebiliriz.[1]
Kanıt:
Verilen herhangi bir üçgen için, doğrudan benzer olmak aşağıdaki denklem karşılanmalıdır:
- [1] nerede ℓ, m, k, a1, b1, ve c1 üçgenlerin kenarlarıdır.
Üçgenlerin geri kalanı için aynı model izlenirse, ilk dört üçgen için denklemlerin toplamının ve son dört üçgen için denklemlerin toplamının aynı sonucu verdiği fark edilecektir.[1] Bu nedenle, bir üçgen benzerlik sistemi tanımına göre, seçilen yedi benzer üçgen ne olursa olsun, sekizinci sistemi tatmin edecek ve hepsini doğrudan benzer kılacaktır.[1]
Fotoğraf Galerisi

Doğrudan Benzerlik Örneği

AHC ve BHC üçgenleri arasında iki olay ilişkisi vardır
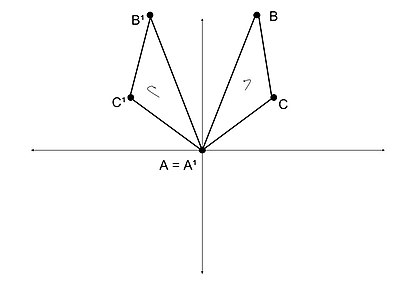
Karşıt benzerlik örneği

Thébault teoremi

Napolyon teoremi

Benzerlik Sistemi Örneği

Benzerlik içermeyen sistem örneği

Dikdörtgen paralel yüzlü
Referanslar
- ^ a b c d e f g h ben j k l m n Ö p q Mauldon, J.G. (Mayıs 1966). "Benzer Üçgenler". Matematik Dergisi. 39 (3): 165–174. doi:10.1080 / 0025570X.1966.11975709.
- ^ Weisstein, Eric. "Benzer". Wolfram MathWorld. Alındı 2018-12-12.
- ^ Gerber Leon (Ekim 1980). "Napolyon Teoremi ve Afin-Düzenli Çokgenler için Paralelkenar Eşitsizliği". American Mathematical Monthly. 87 (8): 644–648. doi:10.1080/00029890.1980.11995110. JSTOR 2320952.
































