Stirling numarası - Stirling number - Wikipedia

İçinde matematik, Stirling numaraları çeşitli analitik ve kombinatoryal sorunlar. Adını alırlar James Stirling, onları 18. yüzyılda tanıtan. İki farklı numara kümesi bu adı taşır: Birinci türden Stirling sayıları ve İkinci türden Stirling sayıları. Bunlara ek olarak, Lah numaraları bazen üçüncü türden Stirling sayıları olarak anılır. Her tür, ilgili maddesinde ayrıntılı olarak anlatılmıştır, bu, aralarındaki ilişkilerin bir açıklaması olarak hizmet eder.

Her üç türün ortak bir özelliği, kombinatoriklerde sıklıkla ortaya çıkan üç farklı polinom dizisini ilişkilendiren katsayıları tanımlamalarıdır. Ayrıca, üçü de bölümlerin sayısı olarak tanımlanabilir. n içine elemanlar k her bir alt küme içinde sıralamayı saymanın farklı yolları olan boş olmayan alt kümeler.

Gösterim

Stirling sayıları için birkaç farklı gösterim kullanılmaktadır. Yaygın gösterimler şunlardır:

${ Displaystyle sol [{n üstte k} sağ] = c (n, k) = | s (n, k) | ,}$

imzasızlar için Birinci türden Stirling sayıları, sayısını sayan permütasyonlar nın-nin n ile elemanlar k ayrık döngüleri,

${ Displaystyle s (n, k) = (- 1) ^ {n-k} sol [{n üstte k} sağ] ,}$

birinci türden sıradan (imzalı) Stirling sayıları için ve

${ displaystyle sol {{ başlar {matris} n k end {matris}} sağ } = S (n, k) = S_ {n} ^ {(k)} ,}$

için İkinci türden Stirling sayıları, bir dizi bölümleme yollarının sayısını sayan n içine elemanlar k boş olmayan alt kümeler.^[1]

Örneğin, toplam ${ displaystyle toplamı _ {k = 0} ^ {n} sol [{n atop k} sağ] = n!}$ toplamı ise tüm permütasyonların sayısıdır ${ displaystyle toplamı _ {k = 0} ^ {n} sol {{ başla {matris} n k end {matris}} sağ } = B_ {n}}$ ... ninci Çan numarası.

Abramowitz ve Stegun büyük S ve a harfini kullanın Siyah mektup S, sırasıyla birinci ve ikinci tür Stirling sayısı için. Parantezlerin ve parantezlerin gösterimi, benzer şekilde iki terimli katsayılar, 1935 yılında Jovan Karamata ve daha sonra tarafından tanıtıldı Donald Knuth. (Parantez gösterimi, için ortak bir gösterimle çelişir Gauss katsayıları.^[2]) Bu tür bir gösterim için matematiksel motivasyonun yanı sıra ek Stirling sayı formülleri aşağıdaki sayfada bulunabilir: Stirling sayıları ve üstel üreten fonksiyonlar.

Düşen ve yükselen faktörlerin genişlemeleri

Stirling sayıları, genişlemelerinde katsayıları ifade eder. düşen ve yükselen faktorler (Pochhammer sembolü olarak da bilinir) polinomlar olarak.

Yani düşen faktör, olarak tanımlandı ${ displaystyle (x) _ {n} = x (x-1) cdots (x-n + 1)}$, bir polinomdur x derece n kimin genişlemesi

${ displaystyle (x) _ {n} = toplam _ {k = 0} ^ {n} s (n, k) x ^ {k}}$

katsayı olarak birinci türden (işaretli) Stirling sayıları ile.

Bunu not et (x)₀ = 1 çünkü bir boş ürün. Kombinatoryalistler ayrıca bazen notasyonu kullanın ${ displaystyle x ^ { underline {n}}}$ düşen faktör için ve ${ displaystyle x ^ { overline {n}}}$ yükselen faktör için.^[3] (Kafa karıştırıcı bir şekilde, çoğunun kullandığı Pochhammer sembolü düşme factorials kullanılır özel fonksiyonlar için yükselen faktöriyeller.)

Benzer şekilde, yükselen faktör, olarak tanımlandı ${ displaystyle x ^ {(n)} = x (x + 1) cdots (x + n-1)}$, bir polinomdur x derece n kimin genişlemesi

${ displaystyle x ^ {(n)} = toplam _ {k = 0} ^ {n} sol [{n atop k} sağ] x ^ {k}}$

katsayı olarak birinci türden işaretsiz Stirling sayıları ile bir genişleme diğerinden elde edilebilir. ${ displaystyle x ^ {(n)} = (- 1) ^ {n} (- x) _ {n}}$.

İkinci türden Stirling sayıları ters ilişkileri ifade eder:

${ displaystyle x ^ {n} = toplam _ {k = 0} ^ {n} sol {{ başlar {matris} n k end {matris}} sağ } (x) _ { k}}$

ve

${ displaystyle x ^ {n} = toplam _ {k = 0} ^ {n} (- 1) ^ {nk} sol {{ başla {matris} n k end {matris}} sağ } x ^ {(k)}.}$

Baz katsayılarının değişimi olarak

Setini göz önünde bulundurarak polinomlar (belirsiz) değişkende x vektör uzayı olarak, üç dizinin her biri

${ displaystyle x ^ {0}, x ^ {1}, x ^ {2}, x ^ {3}, cdots quad (x) _ {0}, (x) _ {1}, (x) _ {2}, cdots quad x ^ {(0)}, x ^ {(1)}, x ^ {(2)}, cdots}$

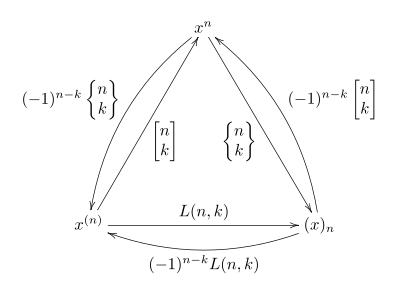
bir temel Yani, içindeki her polinom x toplam olarak yazılabilir ${ displaystyle a_ {0} x ^ {(0)} + a_ {1} x ^ {(1)} + noktalar + a_ {n} x ^ {(n)}}$ bazı benzersiz katsayılar için ${ displaystyle a_ {i}}$ (diğer iki temel için benzer şekilde) Yukarıdaki ilişkiler daha sonra esas değişikliği aşağıda özetlendiği gibi aralarında değişmeli diyagram:

İki dip değişikliğinin katsayıları, Lah numaraları Herhangi bir temeldeki katsayılar benzersiz olduğundan, Stirling sayıları bu şekilde tanımlanabilir, çünkü katsayılar bir temelin polinomlarını diğerine göre ifade eder, yani benzersiz sayılar ${ displaystyle x ^ {n}}$ Düşen ve yükselen faktörlerle yukarıdaki gibi.

Düşen faktöriyeller, ölçeklendirmeye kadar aynı polinomları tanımlar. iki terimli katsayılar: ${ displaystyle textstyle { binom {x} {k}} = { frac {(x) _ {k}} {k!}}}$. Standart esaslar arasındaki değişiklikler ${ displaystyle textstyle x ^ {0}, x ^ {1}, x ^ {2}, noktalar}$ ve temel ${ displaystyle textstyle { binom {x} {0}}, { binom {x} {1}}, { binom {x} {2}}, noktalar}$ bu nedenle benzer formüllerle açıklanmaktadır:

${ displaystyle x ^ {n} = sum _ {k = 0} ^ {n} { begin {Bmatrix} n k end {Bmatrix}} k! { binom {x} {k}}}$ ve ${ displaystyle { binom {x} {n}} = toplam _ {k = 0} ^ {n} { frac {s (n, k)} {n!}} x ^ {k}}$.

Ters matrisler olarak

Birinci ve ikinci türdeki Stirling sayıları birbirinin tersi olarak kabul edilebilir:

${ displaystyle toplamı _ {j geq 0} s (n, j) S (j, k) = toplamı _ {j geq 0} (- 1) ^ {nj} { başla {bmatrix} n j end {bmatrix}} { begin {Bmatrix} j k end {Bmatrix}} = delta _ {nk}}$

ve

${ displaystyle toplamı _ {j geq 0} S (n, j) s (j, k) = toplamı _ {j geq 0} (- 1) ^ {jk} { başlar {Bmatrix} n j end {Bmatrix}} { begin {bmatrix} j k end {bmatrix}} = delta _ {nk},}$

nerede ${ displaystyle delta _ {nk}}$ ... Kronecker deltası. Bu iki ilişki, matris ters ilişkileri olarak anlaşılabilir. Yani izin ver s ol alt üçgen matris matris elemanları olan birinci türden Stirling sayılarının${ displaystyle s_ {nk} = s (n, k). ,}$ ters Bu matrisin S, alt üçgen matris Girişleri olan ikinci türden Stirling sayılarının sayısı ${ displaystyle S_ {nk} = S (n, k).}$ Sembolik olarak bu yazılmıştır

${ displaystyle s ^ {- 1} = S ,}$

olmasına rağmen s ve S sonsuzdur, dolayısıyla bir çarpım girişini hesaplamak sonsuz bir toplam içerir, bu matris çarpımları çalışır çünkü bu matrisler daha düşük üçgendir, bu nedenle toplamdaki yalnızca sonlu bir terim sıfırdan farklıdır.

Misal

Düşen faktöriyeller temelinde bir polinomu ifade etmek, ardışık tam sayılarda değerlendirilen polinomun toplamlarını hesaplamak için kullanışlıdır.Gerçekten, düşen faktöriyelin toplamı, başka bir düşen faktör olarak ifade edilir ( k ≠ -1)

${ displaystyle toplamı _ {0 leq i$

Bu, integrale benzer ${ displaystyle textstyle int _ {0} ^ {n} x ^ {k} = { frac {n ^ {k + 1}} {k + 1}}}$, ancak toplamın tam sayılardan fazla olması gerekir ben kesinlikle daha az n.

Örneğin, tamsayıların dördüncü kuvvetlerinin toplamı n (bu sefer n dahil), şudur:

${ displaystyle { begin {align} & sum _ {i = 0} ^ {n} i ^ {4} = sum _ {i = 0} ^ {n} sum _ {k = 0} ^ { 4} { begin {Bmatrix} 4 k end {Bmatrix}} (i) _ {k} = sum _ {k = 0} ^ {4} { begin {Bmatrix} 4 k end {Bmatrix}} { frac {(n + 1) _ {k + 1}} {k + 1}} = & = { frac { {{ begin {smallmatrix} 4 1 end { smallmatrix}} }} {2}} (n + 1) _ {2} + { frac { {{ begin {smallmatrix} 4 2 end {smallmatrix}} }} {3}} ( n + 1) _ {3} + { frac { {{ begin {smallmatrix} 4 3 end {smallmatrix}} }} {4}} (n + 1) _ {4} + { frac { {{ begin {smallmatrix} 4 4 end {smallmatrix}} }} {5}} (n + 1) _ {5} = & = { frac {1} {2} } (n + 1) _ {2} + { frac {7} {3}} (n + 1) _ {3} + { frac {6} {4}} (n + 1) _ {4} + { frac {1} {5}} (n + 1) _ {5} end {hizalı}}}$

Burada Stirling sayıları, 4 öğenin bölüm sayısı olarak tanımlarından hesaplanabilir. k boş olmayan etiketlenmemiş alt kümeler.

Aksine, toplam ${ displaystyle toplamı _ {i = 0} ^ {n} i ^ {k}}$ standart olarak verilir Faulhaber formülü genel olarak daha karmaşık olan.

Lah numaraları

Lah numaraları ${ displaystyle L (n, k) = {n-1 k-1} seçin { frac {n!} {k!}}}$ bazen üçüncü türden Stirling sayıları olarak adlandırılır.^[4]Kongre tarafından, ${ displaystyle L (0,0) = 1}$ ve ${ displaystyle L (n, k) = 0}$ Eğer ${ displaystyle n> k}$ veya ${ displaystyle k = 0$.

Bu sayılar, düşen faktörleri artan faktörlere göre ifade eden katsayılardır ve bunun tersi de geçerlidir:

${ displaystyle x ^ {(n)} = toplamı _ {k = 0} ^ {n} L (n, k) (x) _ {k} quad}$ ve ${ displaystyle quad (x) _ {n} = toplam _ {k = 0} ^ {n} (- 1) ^ {n-k} L (n, k) x ^ {(k)}.}$

Yukarıdaki gibi, bu, üsler arasındaki temel değişikliğini ifade ettikleri anlamına gelir. ${ displaystyle (x) _ {0}, (x) _ {1}, (x) _ {2}, cdots}$ ve ${ displaystyle x ^ {(0)}, x ^ {(1)}, x ^ {(2)}, cdots}$, diyagramın tamamlanması.Özellikle, bir formül diğerinin tersidir, böylece:

${ displaystyle toplamı _ {j} L (n, j) cdot (-1) ^ {j-k} L (j, k) = delta _ {nk}.}$

Benzer şekilde, örneğin temeli değiştirmek ${ displaystyle x ^ {(n)}}$ -e ${ displaystyle x ^ {n}}$ baz değişikliği ile ${ displaystyle x ^ {n}}$ -e ${ displaystyle (x) _ {n}}$ esas değişikliğini doğrudan ${ displaystyle x ^ {(n)}}$ -e ${ displaystyle (x) _ {n}}$:

${ displaystyle L (n, k) = toplam _ {j} { begin {bmatrix} n j end {bmatrix}} { begin {Bmatrix} j k end {Bmatrix}},}$

Matrisler açısından, eğer ${ displaystyle L}$ matrisi girişlerle gösterir ${ displaystyle L_ {nk} = L (n, k)}$ ve ${ displaystyle L ^ {-}}$ matrisi girdilerle gösterir ${ displaystyle L_ {nk} ^ {-} = (- 1) ^ {n-k} L (n, k)}$, o zaman biri diğerinin tersidir: ${ displaystyle L ^ {-} = L ^ {- 1}}$Benzer şekilde, birinci türden işaretsiz Stirling sayılarının matrisini ikinci türden Stirling sayılarının matrisiyle oluşturmak Lah sayılarını verir: ${ displaystyle L = | s | cdot S}$.

Sayılar ${ displaystyle textstyle { başlar {Bmatrix} n k end {Bmatrix}}, { begin {bmatrix} n k end {bmatrix}}, L (n, k)}$ bölüm sayısı olarak tanımlanabilir n içine elemanlar k Her biri sırasız olan boş olmayan etiketlenmemiş alt kümeler, döngüsel olarak sıralı veya doğrusal sıralı. Bu özellikle aşağıdaki eşitsizlikleri ifade eder:

${ displaystyle { begin {Bmatrix} n k end {Bmatrix}} leq { begin {bmatrix} n k end {bmatrix}} leq L (n, k).}$

Simetrik formüller

Abramowitz ve Stegun, birinci ve ikinci türün Stirling sayılarını ilişkilendiren aşağıdaki simetrik formülleri verir.^[5]

${ displaystyle s (n, k) = toplamı _ {j = 0} ^ {nk} (- 1) ^ {j} {n-1 + j n-k + j} {2n-k seçin nkj} S (n-k + j, j)}$

ve

${ displaystyle S (n, k) = toplam _ {j = 0} ^ {nk} (- 1) ^ {j} {n-1 + j n-k + j} {2n-k seçin nkj} s (n-k + j, j).}$

Negatif integral değerlere sahip Stirling sayıları

Stirling sayıları negatif integral değerlerine kadar uzatılabilir, ancak tüm yazarlar bunu aynı şekilde yapmaz.^[6][7][8] Uygulanan yaklaşım ne olursa olsun, birinci ve ikinci tür Stirling sayılarının ilişkilerle bağlantılı olduğuna dikkat etmek önemlidir:

${ displaystyle sol [{n atop k} sağ] = sol {{ başlar {matris} -k - n end {matris}} sağ } , qquad { text { ve}} qquad left {{ begin {matrix} n k end {matrix}} right } = left [{- k atop -n} sağ]}$

ne zaman n ve k negatif olmayan tam sayılardır. Bu yüzden aşağıdaki tabloya sahibiz ${ displaystyle sol [{- n atop -k} sağ]}$:

Donald Knuth^[8] daha genel Stirling sayılarını bir Tekrarlama ilişkisi tüm tam sayılara. Bu yaklaşımda, ${ displaystyle sol [{n üstte k} sağ]}$ ve ${ displaystyle sol {{ başlar {matris} n k end {matris}} sağ }}$ sıfır ise n negatif ve k negatif değildir veya eğer n negatif değildir ve k negatiftir ve bizde hiç tamsayılar n ve k,

${ displaystyle sol [{n atop k} sağ] = sol {{ başlar {matris} -k - n end {matris}} sağ } , qquad { text { ve}} qquad left {{ begin {matrix} n k end {matrix}} right } = left [{- k atop -n} sağ]}$.

Öte yandan, pozitif tam sayılar için n ve k, David Branson^[7] tanımlı ${ displaystyle sol [{- n atop -k} sağ]}$, ${ displaystyle sol {{ başlar {matris} -n - k son {matris}} sağ }}$, ${ displaystyle sol [{{- n} atop k} sağ]}$, ve ${ displaystyle sol {{ başlar {matris} -n k end {matris}} sağ }}$ (Ama değil ${ displaystyle sol [{n atop -k} sağ]}$ veya ${ displaystyle sol {{ başlar {matris} n - k son {matris}} sağ }}$). Bu yaklaşımda, aşağıdaki uzantıya sahiptir. Tekrarlama ilişkisi Birinci türden Stirling sayıları:

${ displaystyle sol [{- n üstte k} sağ] = { frac {(-1) ^ {n + 1}} {n!}} toplamı _ {i = 1} ^ {n} ( -1) ^ {i + 1} { frac {n i seçin} {i ^ {k}}}}$,

Örneğin, ${ displaystyle sol [{- 5 üstte k} sağ] = { frac {5 - { frac {10} {2 ^ {k}}} + { frac {10} {3 ^ {k} }} - { frac {5} {4 ^ {k}}} + { frac {1} {5 ^ {k}}}} {120}}}$. Bu, aşağıdaki değerler tablosuna götürür ${ displaystyle sol [{- n üstte k} sağ]}$.

k n	0	1	2	3	4
−1	1	1	1	1	1
−2	${ displaystyle { tfrac {-1} {2}}}$	${ displaystyle { tfrac {-3} {4}}}$	${ displaystyle { tfrac {-7} {8}}}$	${ displaystyle { tfrac {-15} {16}}}$	${ displaystyle { tfrac {-31} {32}}}$
−3	${ displaystyle { tfrac {1} {6}}}$	${ displaystyle { tfrac {11} {36}}}$	${ displaystyle { tfrac {85} {216}}}$	${ displaystyle { tfrac {575} {1296}}}$	${ displaystyle { tfrac {3661} {7776}}}$
−4	${ displaystyle { tfrac {-1} {24}}}$	${ displaystyle { tfrac {-25} {288}}}$	${ displaystyle { tfrac {-415} {3456}}}$	${ displaystyle { tfrac {-5845} {41472}}}$	${ displaystyle { tfrac {-76111} {497664}}}$
−5	${ displaystyle { tfrac {1} {120}}}$	${ displaystyle { tfrac {137} {7200}}}$	${ displaystyle { tfrac {12019} {432000}}}$	${ displaystyle { tfrac {874853} {25920000}}}$	${ displaystyle { tfrac {58067611} {1555200000}}}$

Bu durumda ${ displaystyle toplamı _ {n = -1} ^ {- infty} sol [{- n atop -k} sağ] = B_ {k}}$ nerede ${ displaystyle B_ {k}}$ bir Çan numarası ve böylece negatif Bell sayıları şu şekilde tanımlanabilir: ${ displaystyle toplamı _ {n = -1} ^ {- infty} sol [{- n üstte k} sağ] = B _ {- k}}$. Örneğin, bu, ${ displaystyle toplamı _ {n = -1} ^ {- infty} sol [{- n üstte 2} sağ] = B _ {- 2} = 0,421773 ldots}$.

Ayrıca bakınız

• Bell polinomları
• Katalan numarası
• Döngüler ve sabit noktalar
• Lah numarası
• Pochhammer sembolü
• Polinom dizisi
• Stirling dönüşümü
• Touchard polinomları

Referanslar

daha fazla okuma

• Adamchik Victor (1997). "Stirling Sayıları ve Euler Toplamları Üzerine" (PDF). Hesaplamalı ve Uygulamalı Matematik Dergisi. 79: 119–130. doi:10.1016 / s0377-0427 (96) 00167-7.
• Benjamin, Arthur T .; Preston, Gregory O .; Quinn, Jennifer J. (2002). "Harmonik Sayılarla Stirling Karşılaşması" (PDF). Matematik Dergisi. 75 (2): 95–103. CiteSeerX  10.1.1.383.722. doi:10.2307/3219141. JSTOR  3219141.
• Boyadzhiev, Khristo N. (2012). "İkinci türden Stirling sayılarıyla yakın karşılaşmalar" (PDF). Matematik Dergisi. 85 (4): 252–266. arXiv:1806.09468. doi:10.4169 / math.mag.85.4.252.
• Comtet, Louis (1970). "Valeur de s(n, k)". Analiz et Combinatoire, Tome Second (Fransızca): 51.
• Comtet, Louis (1974). İleri Kombinatorikler: Sonlu ve Sonsuz Genişleme Sanatı. Dordrecht-Holland / Boston-ABD.: Reidel Yayıncılık Şirketi.
• Hsien-Kuei Hwang (1995). "Birinci Türün Stirling Sayıları için Asimptotik Genişletmeler". Kombinatoryal Teori Dergisi, Seri A. 71 (2): 343–351. doi:10.1016/0097-3165(95)90010-1.
• Knuth, D.E. (1992), "Gösterim üzerine iki not", Amer. Matematik. Aylık, 99 (5): 403–422, arXiv:math / 9205211, doi:10.2307/2325085, JSTOR  2325085
• Miksa, Francis L. (Ocak 1956). "Birinci türden Stirling sayıları: UMT Dosyasına yatırılan daktiloyla yazılmış el yazmasından çoğaltılmış 27 yaprak". Matematiksel Tablolar ve Hesaplamaya Diğer Yardımlar: Tabloların ve Kitapların İncelemeleri ve Açıklamaları. 10 (53): 37–38. JSTOR  2002617.
• Miksa, Francis L. (1972) [1964]. "Kombinatoryal Analiz, Tablo 24.4, İkinci Türün Stirling Sayıları". Abramowitz, Milton'da; Stegun, Irene A. (editörler). Matematiksel Fonksiyonlar El Kitabı (Formüller, Grafikler ve Matematiksel Tablolar ile). 55. ABD Ticaret Bakanlığı, Ulusal Standartlar Bürosu, Uygulamalı Matematik. s. 835.
• Mitrinović, Dragoslav S. (1959). "Stirling de première espèce et les polinômes de Stirling" (PDF). Publications de la Faculté d'Electrotechnique de l'Université de Belgrade, Série Mathématiques et Physique (Fransızca) (23): 1–20. ISSN  0522-8441.
• O'Connor, John J .; Robertson, Edmund F. (Eylül 1998). "James Stirling (1692–1770)".
• Sixdeniers, J. M .; Penson, K. A .; Solomon, A.I. (2001). "Hipergeometrik Üslemeden Genişletilmiş Bell ve Stirling Sayıları" (PDF). Tamsayı Dizileri Dergisi. 4: 01.1.4.
• Spivey, Michael Z. (2007). "Kombinatoryal toplamlar ve sonlu farklar". Ayrık Matematik. 307 (24). sayfa 3130–3146. doi:10.1016 / j.disc.2007.03.052.
• Sloane, N.J.A. (ed.). "Dizi A008275 (Birinci türden Stirling sayıları)". Tam Sayı Dizilerinin Çevrimiçi Ansiklopedisi. OEIS Vakfı.
• Sloane, N.J.A. (ed.). "Sıra A008277 (2. türden Stirling sayıları)". Tam Sayı Dizilerinin Çevrimiçi Ansiklopedisi. OEIS Vakfı.
• "Birinci türden Stirling sayıları, s (n, k)". PlanetMath.
• "İkinci türden Stirling sayıları, S (n, k)". PlanetMath.