Köşe transfer matrisi - Corner transfer matrix

İçinde Istatistik mekaniği, köşe transfer matrisi Kafese bir kadran eklemenin etkisini açıklar. Tarafından tanıtıldı Rodney Baxter 1968'de Kramers-Wannier satırdan satıra transfer matrisinin bir uzantısı olarak, güçlü bir çalışma yöntemi sağlar kafes modelleri. Köşe transfer matrisleri ile yapılan hesaplamalar, Baxter'ın sert altıgen modeli 1980'de.

Tanım

Bir IRF (etkileşim-yuvarlak-yüz) modelini, yani bir kare kafes modeli düşünün. çevirmek σ_ben her siteye atanmış ben ve etkileşimler ortak bir yüzün etrafındaki dönüşlerle sınırlıdır. Toplam enerji şu şekilde verilsin

${displaystyle E = sum _ {all atop faces} epsilon left (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight),}$

her yüz için çevredeki siteler nerede ben, j, k ve l aşağıdaki gibi düzenlenmiştir:

İle bir kafes için N siteler, bölme fonksiyonu dır-dir

${displaystyle Z_ {N} = sum _ {all atop spins} prod _ {all atop faces} wleft (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight),}$

toplamın olası tüm döndürme yapılandırmalarının üzerinde olduğu ve w Boltzmann ağırlığı

${displaystyle wleft (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight) = exp sol (-epsilon sol (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight) / k_ {B} Sıkı).}$

Gösterimi basitleştirmek için bir ferromanyetik Ising tipi kafes burada her bir dönüş +1 veya -1 değerine sahiptir ve temel durum tüm dönüşler tarafından verilir (yani, kafes üzerindeki tüm dönüşler +1 değerine sahip olduğunda toplam enerji en aza indirilir). Ayrıca, kafesin 4-kat dönüş simetrisine (sınır koşullarına kadar) sahip olduğunu ve yansımayla değişmez olduğunu varsayıyoruz. Bu basitleştirici varsayımlar çok önemli değildir ve tanımı genel duruma genişletmek görece basittir.

Şimdi aşağıda gösterilen kafes kadranını düşünün:

Üçgenlerle işaretlenmiş dış sınır bölgelerine temel durum dönüşleri atanır (bu durumda +1). Açık dairelerle işaretlenmiş alanlar kadranın iç sınırlarını oluşturur; ilişkili spin setleri {σ₁, ..., σ_m} ve {σ '₁, ..., σ '_m}, nerede σ₁ = σ '₁. Onlar 2kişi^m her bir iç sınır için olası konfigürasyonlar, bu nedenle 2^m×2^m matris girdisi

${displaystyle A_ {sigma | sigma '} = delta sol (sigma _ {1}, sigma _ {1}' ight) toplam _ {iç dönüşler} prod _ {tüm üst yüzler} wleft (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight).}$

Matris Bir, o zaman, verilen kafes kadranı için köşe transfer matrisidir. Dış sınır dönüşleri sabit olduğundan ve toplam tüm iç dönüşlerin üzerinde olduğundan, Bir iç sınır dönüşlerinin bir fonksiyonudur. İfadedeki Kronecker deltası, σ₁ = σ '₁, bu nedenle yapılandırmaları uygun şekilde sıralayarak Bir blok diyagonal matris olarak:

${displaystyle {egin {array} {cccc} && {egin {array} {ccccc} sigma _ {1} '= + 1 &&&& sigma _ {1}' = - 1end {array}} A & = & left [{egin {array} {ccccccc} &&& | & A _ {+} && | && 0 &&& | - & - & - & | & - & - & - &&& | & 0 && | && A _ {-} &&& | son {dizi}} ight] & {egin {dizi} {c} sigma _ {1} = + 1 sigma _ {1} = - 1son {dizi}} son {dizi}}}$

Köşe transfer matrisleri, basit bir şekilde bölme fonksiyonuyla ilişkilidir. Basitleştirilmiş örneğimizde, σ, σ ', σ "ve σ'" iç sınır spin kümelerinin farklı olmasına izin verilen kafes çeyreğinin dört döndürülmüş kopyasından tam kafesi oluşturuyoruz:

Bölüm fonksiyonu daha sonra köşe transfer matrisi cinsinden yazılır Bir gibi

${displaystyle Z_ {N} = toplam _ {sigma, sigma ', sigma' ', sigma' ''} A_ {sigma | sigma '} A_ {sigma' | sigma ''} A_ {sigma '' | sigma '' ' } A_ {sigma '' '| sigma} = {extrm {tr}} A ^ {4}.}$

Tartışma

Özyineleme ilişkisi

Bir köşe transfer matrisi Bir_2^m (bir m×m kadran) daha küçük köşe transfer matrisleri cinsinden ifade edilebilir Bir_2^m-1 ve Bir_2^m-2 (azaltılmış (m-1)×(m-1) ve (m-2)×(m-2) kadranlar sırasıyla). Bu yineleme ilişkisi, prensip olarak, sonlu büyüklükteki herhangi bir kafes kadranı için köşe transfer matrisinin yinelemeli hesaplamasına izin verir.

Sıradan sıraya benzerleri gibi, köşe transfer matrisleri de kafese tek bir yüz eklemeye karşılık gelen yüz transfer matrislerine çarpanlarına ayrılabilir. Daha önce verilen kafes kadranı için, yüz transfer matrisleri boyut 2'dir.^m×2^m ve giriş açısından tanımlanmış

${displaystyle left (U_ {i} ight) _ {sigma | sigma '} = delta left (sigma _ {1}, sigma _ {1}' ight) cdots delta left (sigma _ {i-1}, sigma _ { i-1} 'ight) wleft (sigma _ {i}, sigma _ {i + 1}, sigma _ {i}', sigma _ {i-1} ight) delta sol (sigma _ {i + 1}, sigma _ {i + 1} 'ight) cdots delta left (sigma _ {m}, sigma _ {m}' ight),}$

nerede 2 ≤ ben ≤ m+1. Dış sınırın yakınında, özellikle elimizde

${displaystyle left (U_ {m} ight) _ {sigma | sigma '} = delta left (sigma _ {1}, sigma _ {1}' ight) cdots delta left (sigma _ {m-1}, sigma _ { m-1} 'ight) wleft (sigma _ {m}, + 1, sigma _ {m}', sigma _ {m-1} ight)}$

${displaystyle left (U_ {m + 1} ight) _ {sigma | sigma '} = delta left (sigma _ {1}, sigma _ {1}' ight) cdots delta left (sigma _ {m}, sigma _ { m} 'ight) wleft (+ 1, + 1, + 1, sigma _ {m} ight).}$

Yani köşe transfer matrisi Bir faktörlere göre

${displaystyle A = F_ {2} cdots F_ {m + 1},}$

nerede

${displaystyle F_ {j} = U_ {m + 1} cdots U_ {j}.}$

Grafiksel olarak bu şuna karşılık gelir:

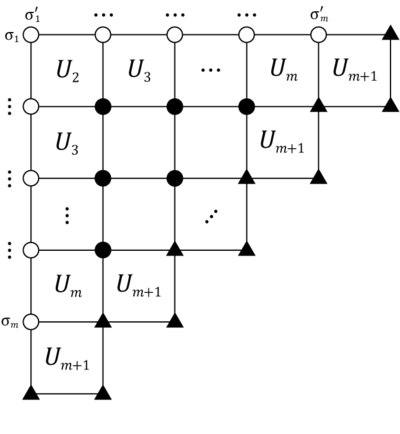
Ayrıca 2'ye de ihtiyacımız var^m×2^m matrisler Bir* ve Bir**, giriş açısından tanımlanmış

${displaystyle left (A ^ {*} ight) _ {sigma | sigma '} = delta left (sigma _ {1}, sigma _ {1}' ight) A_ {sigma _ {2}, ldots, sigma _ {m } | sigma _ {2} ', ldots, sigma _ {m}'},}$

${displaystyle left (A ^ {**} ight) _ {sigma | sigma '} = delta left (sigma _ {1}, sigma _ {1}' ight) delta left (sigma _ {2}, sigma _ {2 } 'ight) A_ {sigma _ {3}, ldots, sigma _ {m} | sigma _ {3}', ldots, sigma _ {m} '},}$

nerede Bir Girişleri RHS'de görünen matrisler boyut 2'dir^m-1×2^m-1 ve 2^m-2×2^m-2 sırasıyla. Bu daha açık bir şekilde şöyle yazılır:

${displaystyle A ^ {*} = I_ {2} otimes A_ {2 ^ {m-1}} = sol [{egin {array} {cc} A & 0 0 & Aend {array}} ight],}$

${displaystyle A ^ {**} = I_ {2} otimes I_ {2} otimes A_ {2 ^ {m-2}} = sol [{egin {array} {cccc} A & 0 & 0 & 0 0 & A & 0 & 0 0 & 0 & A & 0 0 & 0 & 0 & Aend {array} } ight].}$

Şimdi tanımlarından Bir, Bir*, Bir**, U_ben ve F_j, sahibiz

${displaystyle A ^ {*} = F_ {3} cdots F_ {m + 1}, A ^ {**} = F_ {4} cdots F_ {m + 1}}$

${displaystyle Rightarrow A = F_ {2} A ^ {*}, A ^ {*} = F_ {3} A ^ {**}}$

${displaystyle Rightarrow A = A ^ {*} sol (A ^ {**} ight) ^ {- 1} U_ {2} A ^ {*},}$

için özyineleme ilişkisini veren Bir_2^m açısından Bir_2^m-1 ve Bir_2^m-2.

Çapraz form

Hesaplamaları yapmak için köşe transfer matrislerini kullanırken, bunun yerine köşegen formlarıyla çalışmak hem analitik hem de sayısal olarak uygundur. Bunu kolaylaştırmak için, özyineleme ilişkisi doğrudan şu terimlerle yeniden yazılabilir: çapraz formlar ve özvektör matrisleri nın-nin Bir, Bir* ve Bir**.

Örneğimizdeki kafesin yansıma değişmez olduğunu hatırlayarak,

${displaystyle wleft (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight) = wleft (sigma _ {k}, sigma _ {j}, sigma _ {i}, sigma _ {l} ight) = wleft (sigma _ {i}, sigma _ {l}, sigma _ {k}, sigma _ {j} ight),}$

bunu görüyoruz Bir simetrik bir matristir (yani köşegenleştirilebilir bir ortogonal matris ). Bu yüzden yazıyoruz

${displaystyle A = alpha _ {m} PA_ {d} P ^ {T},}$

nerede Bir_d köşegen bir matristir (sayısal olarak en büyük girişi 1 olacak şekilde normalleştirilmiştir), α_m en büyük özdeğerdir Bir, ve P^TP = ben. Aynı şekilde Bir* ve Bir**, sahibiz

${displaystyle A ^ {*} = alpha _ {m-1} P ^ {*} A_ {d} ^ {*} sol (P ^ {*} sağ) ^ {T},}$

${displaystyle A ^ {**} = alpha _ {m-2} P ^ {**} A_ {d} ^ {**} sol (P ^ {**} sağ) ^ {T},}$

nerede Bir_d*, Bir_d**, P* ve P** benzer bir şekilde tanımlanmıştır Bir* ve Bir**, yani daha küçük (normalleştirilmiş) diyagonal formlar ve (ortogonal) özvektör matrisleri açısından Bir_2^m-1 ve Bir_2^m-2.

Bu köşegenleştirmeleri özyineleme bağıntısına yerleştirerek elde ederiz

${displaystyle A_ {t} = kappa RA_ {d} R ^ {T},}$

nerede

${displaystyle kappa = {frac {alpha _ {m} alpha _ {m-2}} {alpha _ {m-1} ^ {2}}},}$

${displaystyle R = sol (P ^ {*} sağ) ^ {T} P,}$

${displaystyle A_ {t} = A_ {d} ^ {*} sol (R ^ {*} ight) ^ {T} sol (A_ {d} ^ {**} ight) ^ {- 1} U_ {2} R ^ {*} A_ {d} ^ {*}.}$

Şimdi Bir_t aynı zamanda simetriktir ve şu durumlarda hesaplanabilir: Bir_d*, Bir_d** ve R* bilinmektedir; köşegenleştirme Bir_t daha sonra normalleştirilmiş çapraz şeklini verir Bir_d, en büyük öz değeri κve ortogonal özvektör matrisi R.

Başvurular

Spin beklenti değeri

Köşe transfer matrisleri (veya köşegen formları), spin gibi miktarları hesaplamak için kullanılabilir. beklenti değeri kafesin derinliklerinde belirli bir yerde. Daha önce verilen tam kafes için, merkezi sitedeki eğirme beklentisi değeri şu şekilde verilir:

${displaystyle leftlangle sigma _ {1} ightangle = {frac {1} {Z_ {N}}} toplam _ {all atop spins} sigma _ {1} prod _ {all atop faces} wleft (sigma _ {i}, sigma _ {j}, sigma _ {k}, sigma _ {l} ight).}$

Yapılandırmalar öyle sipariş edildiğinde Bir daha önce olduğu gibi blok diyagonaldir, 2 tanımlayabiliriz^m×2^m Diyagonal matris

${displaystyle S = left [{egin {dizi} {cc} I & 0 0 & -Iend {dizi}} ight],}$

öyle ki

${displaystyle leftlangle sigma _ {1} ightangle = {frac {{extrm {tr}} SA ^ {4}} {{extrm {tr}} A ^ {4}}} = {frac {{extrm {tr}} alfa _ {m} ^ {4} PSA ^ {4} P ^ {T}} {{extrm {tr}} alpha _ {m} ^ {4} PA ^ {4} P ^ {T}}} = {frac {{extrm {tr}} SA_ {d} ^ {4}} {{extrm {tr}} A_ {d} ^ {4}}}.}$

Site başına bölümleme işlevi

Kafes modelleri için bir diğer önemli miktar, site başına bölümleme fonksiyonudur. termodinamik limit ve şu şekilde yazılmıştır

${displaystyle kappa = lim _ {Nightarrow infty} sol (Z_ {N} ight) ^ {1 / N}.}$

Örneğimizde bu,

${displaystyle kappa = lim _ {Nightarrow infty} sol (alpha _ {m} ^ {4} {extrm {tr}} A_ {d} ^ {4} ight) ^ {1 / N} sim alpha _ {m} ^ {4 / N},}$

tr'den beri Bir_d⁴ yakınsak bir toplamdır m → ∞ ve Bir_d sonsuz boyutlu hale gelir. Ayrıca yüzlerin sayısı 2m(m+1) site sayısına yaklaşır N termodinamik sınırda, bu nedenle elimizde

${displaystyle alpha _ {m} sim kappa ^ {mleft (a + 1ight) / 2},}$

önceki denklem verme ile tutarlı olan κ için en büyük özdeğer olarak Bir_t. Başka bir deyişle, site başına bölümleme fonksiyonu, termodinamik limitte köşe transfer matrisleri için tam olarak köşegenleştirilmiş özyineleme ilişkisi ile verilmektedir; bu izin verir κ yinelemeli hesaplama süreciyle tahmin edilecek Bir_d büyük bir kafes için.

Bununla birlikte, ilgili matrisler boyut olarak katlanarak büyür ve gerçek sayısal hesaplamalarda her adımda kesilmeleri gerekir. Bunu yapmanın bir yolu, n bazı sabitler için her adımda en büyük özdeğerler n. Çoğu durumda, alınarak elde edilen yaklaşım dizisi n = 1,2,3, ... hızla yakınsar ve tam değere (tam olarak çözülebilir bir model için).

Ayrıca bakınız

• Transfer matrisi yöntemi

Referanslar

• Baxter, R. J. (1981), "Köşe Transfer Matrisleri", Physica A, 106 (1–2): 18–27, Bibcode:1981PhyA..106 ... 18B, doi:10.1016 / 0378-4371 (81) 90203-X
• Baxter, R.J. (1982), İstatistiksel Mekanikte Tam Olarak Çözülmüş Modeller, Londra, İngiltere: Academic Press, ISBN  0-12-083180-5