IEEE 754-1985 - IEEE 754-1985 - Wikipedia

IEEE 754-1985[1] bir endüstriydi standart temsil etmek için kayan nokta sayılar bilgisayarlar 1985'te resmen kabul edildi ve 2008'de yerini aldı. IEEE 754-2008 ve ardından 2019'da küçük bir revizyonla IEEE 754-2019.[2] 23 yılı boyunca, kayan nokta hesaplaması için en yaygın kullanılan formattı. Yazılımda kayan nokta şeklinde uygulandı kütüphaneler ve donanımda, Talimatlar çoğunun CPU'lar ve FPU'lar. İlk entegre devre IEEE 754-1985 olacak olanın taslağını uygulamak, Intel 8087.

IEEE 754-1985, ikili, en yaygın kullanılan ikisi olan dört kesinlik düzeyi için tanımlar sağlar:

SeviyeGenişlikTam hassasiyette menzilHassas[a]
Tek hassasiyet32 bit±1.18×10−38 ± 3.4×1038Yaklaşık 7 ondalık basamak
Çift hassasiyet64 bit±2.23×10−308 ± 1.80'e kadar×10308Yaklaşık 16 ondalık basamak

Standart ayrıca pozitif ve negatif için temsilleri tanımlar sonsuzluk, a "negatif sıfır ", gibi geçersiz sonuçları ele almak için beş istisna sıfıra bölüm özel değerler denir NaN'ler bu istisnaları temsil etmek için, normal olmayan sayılar yukarıda gösterilenden daha küçük sayıları temsil etmek için ve dört yuvarlama modlar.

Sayıların temsili

0.15625 sayısı, tek duyarlıklı IEEE 754-1985 kayan noktalı sayı olarak temsil edilir. Açıklama için metne bakın.
64 bit IEEE 754 kayan noktadaki üç alan

IEEE 754 biçimindeki kayan noktalı sayılar üç alandan oluşur: a işaret biti, bir yanlı üs ve bir kesir. Aşağıdaki örnek, her birinin anlamını göstermektedir.

0.15625 ondalık sayı10 ikili olarak temsil edilen 0.001012 (yani, 1/8 + 1/32). (Abonelikler numarayı gösterir temel.) Benzer bilimsel gösterim, sayıların ondalık noktanın soluna sıfır olmayan tek bir basamağa sahip olacak şekilde yazıldığı yerlerde, bu sayıyı "ikili noktanın" solunda tek bir 1 bit olacak şekilde yeniden yazarız. Kalan bitleri üç pozisyonla kaydırmayı telafi etmek için 2'nin uygun kuvvetiyle çarpıyoruz:

Şimdi kesri ve üssü okuyabiliriz: kesir .01'dir.2 ve üs −3'tür.

Resimlerde gösterildiği gibi, bu numaranın IEEE 754 gösterimindeki üç alan şunlardır:

işaret = 0, çünkü sayı pozitiftir. (1 negatifi belirtir.)
yanlı üs = −3 + "önyargı". İçinde Tek hassasiyetönyargı 127yani bu örnekte yanlı üs 124'tür; içinde çift ​​hassasiyetönyargı 1023, dolayısıyla bu örnekteki yanlı üs 1020'dir.
kesir = .01000…2.

IEEE 754, bir önyargı üs olarak ifade eder, böylece birçok durumda, işaretli olanları karşılaştıran aynı donanımla sayılar rahatlıkla karşılaştırılabilir. 2'nin tamamlayıcısı tamsayılar. Önyargılı bir üs kullanıldığında, iki pozitif kayan noktalı sayıdan daha küçük olanı "daha küçük" çıkacaktır. işaret ve büyüklük tamsayılar. İki kayan noktalı sayının farklı işaretleri varsa, işaret ve büyüklük karşılaştırması yanlı üslerle de çalışır. Bununla birlikte, her iki yanlı üslü kayan nokta sayısı negatifse, sıralama tersine çevrilmelidir. Üs, diyelim ki 2'nin tamamlayıcı sayısı olarak gösterilseydi, iki sayıdan hangisinin daha büyük olduğunu görmek için karşılaştırma yapmak o kadar uygun olmazdı.

Baştaki 1 bit, sıfır dışındaki tüm sayılar baştaki 1 ile başladığından atlanır; baştaki 1 örtüktür ve aslında depolanması gerekmez, bu da "ücretsiz" için fazladan bir hassasiyet verir.

Sıfır

Sıfır sayısı özel olarak temsil edilir:

işaret = 0 için pozitif sıfır, 1 için negatif sıfır.
yanlı üs = 0.
kesir = 0.

Normal olmayan sayılar

Yukarıda açıklanan sayı temsillerine denir normalleştirilmiş, örtük önde gelen ikili rakamın 1 olduğu anlamına gelir. Bir 1 olduğunda hassasiyet kaybını azaltmak için alttan taşma oluştuğunda, IEEE 754 örtük ön basamağı 0 yaparak normalleştirilmiş gösterimde mümkün olandan daha küçük kesirleri temsil etme yeteneğini içerir. normal olmayan. Çok fazla içermiyorlar önemli basamaklar normalleştirilmiş bir sayı olarak, ancak bir sonucun sonucu olduğunda kademeli bir hassasiyet kaybına neden olurlar. aritmetik işlem tam olarak sıfır değildir, ancak normalleştirilmiş bir sayı ile temsil edilemeyecek kadar sıfıra çok yakındır.

Normal olmayan bir sayı, tüm 0 bitlerin önyargılı bir üssüyle temsil edilir; bu, tek hassasiyette (−127 değil) −126 veya çift hassasiyette (−1023 değil) −1022 üssünü temsil eder.[3] Buna karşılık, normal bir sayıyı temsil eden en küçük yanlı üs 1'dir (bkz. örnekler altında).

Sayı olmayanların temsili

Önyargılı üslü alan, bir hesaplamanın sonsuz veya geçersiz bir sonucunu belirtmek için 1 bitin tümü ile doldurulur.

Pozitif ve negatif sonsuzluk

Pozitif ve negatif sonsuzluk şu şekilde temsil edilir:

işaret = 0 pozitif sonsuz için, 1 negatif sonsuz için.
yanlı üs = 1 bitin tümü.
kesir = tümü 0 bit.

NaN

Bazı işlemler kayan nokta aritmetiği negatif bir sayının karekökünü almak gibi geçersizdir. Geçersiz bir sonuca ulaşma eylemine kayan nokta denir istisna. İstisnai bir sonuç, NaN adı verilen özel bir kodla temsil edilir.Sayı değil ". IEEE 754-1985'teki tüm NaN'ler şu biçime sahiptir:

işaret = 0 veya 1.
yanlı üs = tüm 1 bit.
kesir = 0 bitin tümü dışında herhangi bir şey (çünkü tüm 0 bitler sonsuzluğu temsil eder).

Menzil ve hassasiyet

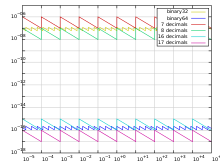
Tek (ikili32) ve çift duyarlıklı (ikili64) sayıların göreli kesinliği, sabit bir sayı kullanan ondalık gösterimlerle karşılaştırıldığında önemli basamaklar. Göreli hassasiyet burada ulp (x)/x, nerede ulp (x) son sırada yer alan birim temsilinde x, yani arasındaki boşluk x ve bir sonraki gösterilebilir sayı.

Kesinlik, iki ardışık mantis gösterimi arasındaki minimum fark olarak tanımlanır; bu nedenle, yalnızca mantiste bir işlevdir; boşluk iki ardışık sayı arasındaki fark olarak tanımlanır.[4]

Tek hassasiyet

Tek hassasiyet sayılar 32 bit kaplar. Tek hassasiyette:

  • Sıfıra en yakın pozitif ve negatif sayılar (üs alanında tüm 0'lar ve kesir alanında ikili değer 1 ile normalleştirilmiş değer ile temsil edilir)
    ±2−23 × 2−126 ≈ ±1.40130×10−45
  • Sıfıra en yakın pozitif ve negatif normalleştirilmiş sayılar (üs alanında 1 ikili değeri ve kesir alanında 0 ile temsil edilir)
    ±1 × 2−126 ≈ ±1.17549×10−38
  • Sıfırdan en uzak sonlu pozitif ve sonlu negatif sayılar (üs alanında 254 ve kesir alanında tüm 1'ler ile temsil edilen)
    ±(2−2−23) × 2127[5] ≈ ±3.40282×1038

Verilen üsler için tek kesinlikte bazı örnek aralık ve boşluk değerleri:

Gerçek Üs (tarafsız)Deneyim (önyargılı)MinimumMaksimumBoşluk
−11260.5≈ 0.999999940395≈ 5,96046e-8
01271≈ 1.999999880791≈ 1.19209e-7
11282≈ 3.999999761581≈ 2.38419e-7
21294≈ 7.999999523163≈ 4.76837e-7
101371024≈ 2047.999877930≈ 1.22070e-4
111382048≈ 4095.999755859≈ 2.44141e-4
231508388608167772151
2415116777216335544302
127254≈ 1.70141e38≈ 3.40282e38≈ 2.02824e31

Örnek olarak 16.777.217, 16.777.216'ya yuvarlanacağı için 32 bitlik kayan nokta olarak kodlanamaz. Bu, kayan nokta aritmetiğinin muhasebe yazılımı için neden uygun olmadığını gösterir. Bununla birlikte, gösterilebilir aralıktaki 2'nin üssü olan tüm tamsayılar, yuvarlama olmaksızın 32 bitlik bir kayan nokta içinde saklanabilir.

Çift hassasiyet

Çift hassasiyet sayılar 64 bit kaplar. Çift hassasiyette:

  • Sıfıra en yakın pozitif ve negatif sayılar (Exp alanındaki tüm 0'larla normalleştirilmiş değer ve Kesir alanındaki 1 ikili değerle temsil edilir)
    ±2−52 × 2−1022 ≈ ±4.94066×10−324
  • Sıfıra en yakın pozitif ve negatif normalleştirilmiş sayılar (Exp alanında 1 ikili değeri ve kesir alanında 0 ile temsil edilir)
    ±1 × 2−1022 ≈ ±2.22507×10−308
  • Sıfırdan en uzak sonlu pozitif ve sonlu negatif sayılar (Exp alanında 2046 ile ve kesir alanındaki tüm 1'ler ile temsil edilir)
    ±(2−2−52) × 21023[5] ≈ ±1.79769×10308

Verilen üsler için çift kesinlikte bazı örnek aralık ve boşluk değerleri:

Gerçek Üs (tarafsız)Deneyim (önyargılı)MinimumMaksimumBoşluk
−110220.5≈ 0.999999999999999888978≈ 1.11022e-16
010231≈ 1.999999999999999777955≈ 2.22045e-16
110242≈ 3.999999999999999555911≈ 4.44089e-16
210254≈ 7.999999999999999111822≈ 8.88178e-16
1010331024≈ 2047.999999999999772626≈ 2.27374e-13
1110342048≈ 4095.999999999999545253≈ 4.54747e-13
521075450359962737049690071992547409911
5310769007199254740992180143985094819822
10232046≈ 8.98847e307≈ 1,79769e308≈ 1,99584e292

Genişletilmiş formatlar

Standart ayrıca, yuvarlama hatalarını en aza indirmek için dahili hesaplamaları nihai sonuç için gerekenden daha yüksek bir hassasiyetle gerçekleştirmek üzere genişletilmiş format (lar) ın kullanılmasını önerir: standart, bu tür formatlar için yalnızca minimum kesinlik ve üs gereksinimlerini belirtir. x87 80 bit genişletilmiş format bu gereksinimleri karşılayan en yaygın olarak uygulanan genişletilmiş biçimdir.

Örnekler

Aşağıda, tek duyarlıklı IEEE 754 gösterimlerinin bazı örnekleri verilmiştir:

TürİşaretGerçek ÜsDeneyim (önyargılı)Üs alanıKesir alanıDeğer
Sıfır0−12600000 0000000 0000 0000 0000 0000 00000.0
Negatif sıfır1−12600000 0000000 0000 0000 0000 0000 0000−0.0
Bir001270111 1111000 0000 0000 0000 0000 00001.0
Eksi bir101270111 1111000 0000 0000 0000 0000 0000−1.0
En küçük normal olmayan sayı*−12600000 0000000 0000 0000 0000 0000 0001±2−23 × 2−126 = ±2−149 ≈ ±1.4×10−45
"Orta" denormalize edilmiş sayı*−12600000 0000100 0000 0000 0000 0000 0000±2−1 × 2−126 = ±2−127 ≈ ±5.88×10−39
En büyük normal olmayan sayı*−12600000 0000111 1111 1111 1111 1111 1111±(1−2−23) × 2−126 ≈ ±1.18×10−38
En küçük normalleştirilmiş sayı*−12610000 0001000 0000 0000 0000 0000 0000±2−126 ≈ ±1.18×10−38
En büyük normalleştirilmiş sayı*1272541111 1110111 1111 1111 1111 1111 1111±(2−2−23) × 2127 ≈ ±3.4×1038
Pozitif sonsuzluk01282551111 1111000 0000 0000 0000 0000 0000+∞
Negatif sonsuzluk11282551111 1111000 0000 0000 0000 0000 0000−∞
Sayı değil*1282551111 1111sıfır olmayanNaN
* İşaret biti 0 veya 1 olabilir.

Kayan noktalı sayıları karşılaştırma

Olası her bit kombinasyonu, bir NaN veya içinde benzersiz bir değere sahip bir sayıdır. afin bir şekilde genişletilmiş gerçek sayı sistemi bazen özel dikkat gerektiren, negatif sıfır ve pozitif sıfır için iki bit kombinasyonu haricinde ilişkili sırası ile birlikte (aşağıya bakınız). ikili gösterim NaN'ler hariç herhangi iki sayının karşılaştırılabileceği özelliğe sahiptir. işaret ve büyüklük tamsayılar (endianness sorunlar geçerlidir). Olarak karşılaştırırken 2'nin tamamlayıcısı tamsayılar: İşaret bitleri farklıysa, negatif sayı pozitif sayıdan önce gelir, bu nedenle 2'nin tamamlayıcısı doğru sonucu verir (negatif sıfır ve pozitif sıfırın eşit kabul edilmesi dışında). Her iki değer de pozitifse, 2'nin tamamlayıcı karşılaştırması yine doğru sonucu verir. Aksi takdirde (iki negatif sayı), doğru FP sıralaması, 2'nin tamamlayıcı sıralamasının tersidir.

Kayan nokta hesaplamalarına özgü yuvarlama hataları, sonuçların tam eşitliğini kontrol etmek için karşılaştırmaların kullanımını sınırlayabilir. Kabul edilebilir bir aralık seçmek karmaşık bir konudur. Yaygın bir teknik, yaklaşık karşılaştırmalar yapmak için bir epsilon karşılaştırma değeri kullanmaktır.[6] Karşılaştırmaların ne kadar yumuşak olduğuna bağlı olarak, ortak değerler şunları içerir: 1e-6 veya 1e-5 tek hassasiyet için ve 1e-14 çift ​​hassasiyet için.[7][8] Diğer bir yaygın teknik, son basamaktaki farkın ne olduğunu kontrol eden ve iki değerin kaç adım uzakta olduğunu etkili bir şekilde kontrol eden ULP'dir.[9]

Negatif sıfır ve pozitif sıfır genel olarak karşılaştırma amaçları için eşit kabul edilse de, bazıları Programlama dili ilişkisel operatörler ve benzer yapılar onları ayrı olarak ele alır. Göre Java Dil Özellikleri,[10] karşılaştırma ve eşitlik operatörleri bunları eşit görürler, ancak Math.min () ve Math.max () karşılaştırma yöntemleri gibi bunları ayırt edin (resmi olarak Java sürüm 1.1 ile başlayıp aslında 1.1.1 ile) eşittir (), karşılaştırmak() ve hatta karşılaştırmak() sınıfların Yüzer ve Çift.

Kayan noktalı sayıları yuvarlama

IEEE standardının dört farklı yuvarlama modu vardır; ilki varsayılandır; diğerleri aranır yönlendirilmiş yuvarlamalar.

  • En Yakına Yuvarla - en yakın değere yuvarlar; sayı ortada düşerse, çift (sıfır) en az anlamlı bit ile en yakın değere yuvarlanır, bu da zamanın% 50'sine yuvarlandığı anlamına gelir ( IEEE 754-2008 bu mod denir roundTiesToEven onu başka bir en yakına yuvarlama modundan ayırmak için)
  • 0'a doğru yuvarla - sıfıra doğru yuvarlama
  • + ∞'a doğru yuvarlayın - pozitif sonsuza doğru yuvarlama
  • −∞'a doğru yuvarla - negatif sonsuza doğru yuvarlama.

Gerçek sayıları genişletmek

IEEE standardı aşağıdakileri kullanır (ve genişletir) afin bir şekilde genişletilmiş gerçek sayı sistemi, ayrı pozitif ve negatif sonsuzluklarla. Taslak hazırlama sırasında, standardın aşağıdakileri içermesi için bir teklif vardı: projeksiyonla genişletilmiş gerçek sayı sistemi, programcılara bir mod seçme seçeneği sağlayarak tek bir işaretsiz sonsuzluk ile. Nihai standardın karmaşıklığını azaltmak adına, projektif mod bırakıldı. Intel 8087 ve Intel 80287 kayan noktalı ortak işlemcilerin her ikisi de bu projektif modu destekler.[11][12][13]

Fonksiyonlar ve yüklemler

Standart işlemler

Aşağıdaki işlevler sağlanmalıdır:

  • Topla, çıkar, çarp, böl
  • Kare kök
  • Kayan nokta kalanı. Bu normal değil modulo işlemi, iki pozitif sayı için negatif olabilir. Tam değerini döndürür x– (yuvarlak (x / y) · y).
  • En yakın tam sayıya yuvarla. Yönsüz yuvarlama için iki tamsayı arasında yarı yolda iken çift tam sayı seçilir.
  • Karşılaştırma işlemleri. Daha belirgin sonuçların yanı sıra, IEEE 754, −∞ = −∞, + ∞ = + ∞ ve x ≠ NaN herhangi x (dahil olmak üzere NaN).

Önerilen işlevler ve yüklemler

  • kopya işareti (x, y) x'i y'nin işaretiyle döndürür, bu nedenle abs (x) eşittir kopya işareti (x, 1.0). Bu, NaN üzerinde aritmetiğe benzer şekilde çalışan birkaç işlemden biridir. İşlev kopya işareti C99 standardında yenidir.
  • −x, işareti ters çevrilmiş olarak x'i döndürür. Bu, bazı durumlarda, özellikle x 0 olduğunda, 0 − x'ten farklıdır. Yani - (0) −0'dır, ancak 0−0'ın işareti yuvarlama moduna bağlıdır.
  • scalb (y, N)
  • logb (x)
  • sonlu (x) a yüklem "x sonlu bir değerdir" için −Inf
  • isnan (x) "x bir NaN'dir" için bir yüklem, "x ≠ x" e eşdeğer
  • x <> y, NaN nedeniyle NOT (x = y) 'den farklı davranışa sahip olduğu ortaya çıktı.
  • sırasız (x, y) "x, y ile sıralanmamışsa", yani x veya y bir NaN olduğunda doğrudur.
  • sınıf (x)
  • sonraki (x, y) x'ten y'ye doğru bir sonraki gösterilebilir değeri döndürür

Tarih

1976'da, Intel bir kayan noktanın geliştirilmesine başlıyordu yardımcı işlemci.[14][15] Intel, çok çeşitli matematik yazılım kitaplıklarında bulunan tüm işlemlerin iyi uygulamalarını içeren bir çip satmayı umuyordu.[14][16]

Projeyi yöneten John Palmer, onları tüm kayan nokta operasyonları için bir standart geliştirmeye çalışmaları gerektiğine ikna etti. İletişim kurdu William Kahan of Kaliforniya Üniversitesi, doğruluğunu artırmaya yardımcı olan Hewlett Packard hesap makineleri. Kahan, Intel'in kayan noktasını kullanmasını önerdi. Digital Equipment Corporation (DEC) VAX. İlk VAX, VAX-11/780 1977'nin sonlarında yeni çıkmıştı ve kayan noktası son derece kabul görüyordu. Bununla birlikte, çiplerini mümkün olan en geniş pazara pazarlamak isteyen Intel, mümkün olan en iyi kayan noktayı istedi ve Kahan teknik özellikleri hazırlamaya devam etti.[14] Kahan başlangıçta kayan nokta tabanının ondalık olmasını önerdi[17] ancak yardımcı işlemcinin donanım tasarımı bu değişikliği yapmak için çok uzaktı.

Intel bünyesindeki çalışma, 'eşit şartlar altında bir oyun alanı' sağlamak için bir standartlaştırma çabası oluşturan diğer satıcıları endişelendirdi. Kahan, Kasım 1977'de düzenlenen ikinci IEEE 754 standartları çalışma grubu toplantısına katıldı. Burada, bir yardımcı işlemci için tasarımlarının standart aritmetik kısmına dayalı bir taslak teklif sunmak için Intel'den izin aldı; Intel'in tasarım kararlarını ve bunların altında yatan gerekçeleri açıklamasına izin verildi, ancak Intel'in uygulama mimarisiyle ilgili hiçbir şey yoktu.[14][15][16][18]

8 bitlik bir üs, çift duyarlıklı sayılar için istenen bazı işlemler için yeterince geniş olmadığından, örn. 32 bitlik iki sayının ürününü saklamak için,[19] Hem Kahraman'ın önerisi hem de DEC'in karşı önerisi, bu nedenle, zaman testinde olduğu gibi 11 bit kullandı 60 bit kayan nokta biçimi of CDC 6600 1965'ten.[15][18][20] Kahraman'ın önerisi, sıfıra bölme koşullarıyla uğraşırken yararlı olan sonsuzluklar için de sağladı; geçersiz işlemlerle uğraşırken yararlı olan sayı olmayan değerler; normal olmayan sayılar alttan taşmanın neden olduğu sorunları azaltmaya yardımcı olan;[18][21][22] ve daha dengeli üssel önyargı Bu, bir sayının karşılığını alırken taşmanın ve eksikliğin önlenmesine yardımcı olabilir.[23][24]

Onaylanmadan önce bile, taslak standart bir dizi üretici tarafından uygulanmıştı.[25][26] 1980'de duyurulan Intel 8087, standart taslağı uygulayan ilk yongaydı.

Intel 8087 kayan noktalı yardımcı işlemci

1980 yılında Intel 8087 çip zaten serbest bırakıldı,[27] ancak DEC, performans kaygıları nedeniyle ve DEC formatını standartlaştırmak için DEC'e rekabet avantajı sağlayacağı için, özellikle normal sayılara karşı çıkmıştır.

Tartışmalar bitti kademeli alt akış bir uzman tarafından işe alınan 1981 yılına kadar sürdü ARALIK muhaliflerin yanında olduğunu değerlendirmek için. DEC, kademeli alt akışın kötü bir fikir olduğunu göstermek için bir çalışma yapmıştı, ancak çalışma tam tersini yaptı ve DEC teslim oldu. 1985'te standart onaylandı, ancak zaten bir yıl önce fiili standart haline gelmişti. birçok üretici tarafından uygulanmaktadır.[15][18][28]

Ayrıca bakınız

Notlar

  1. ^ Kesinlik: Ondalık basamak kesinliğinin sayısı, number_of_mantissa_bits * Log aracılığıyla hesaplanır10(2). Böylece tek ve çift kesinlik için sırasıyla ~ 7.2 ve ~ 15.9.

Referanslar

  1. ^ İkili Kayan Nokta Aritmetiği için IEEE Standardı. 1985. doi:10.1109 / IEEESTD.1985.82928. ISBN  0-7381-1165-1.
  2. ^ "ANSI / IEEE Std 754-2019". 754r.ucbtest.org. Alındı 2019-08-06.
  3. ^ Hennessy (2009). Bilgisayar Organizasyonu ve Tasarımı. Morgan Kaufmann. s.270.
  4. ^ Hossam A. H. Fahmy; Shlomo Waser; Michael J. Flynn, Bilgisayar Aritmetiği (PDF), dan arşivlendi orijinal (PDF) 2010-10-08 tarihinde, alındı 2011-01-02
  5. ^ a b William Kahan. "IEEE 754'ün Durumuyla İlgili Ders Notları" (PDF). 1 Ekim 1997 03:36. Elekt. Müh. & California Bilgisayar Bilimleri Üniversitesi. Alındı 2007-04-12. Alıntı dergisi gerektirir | günlük = (Yardım)
  6. ^ "Godot math_funcs.h". GitHub.com.
  7. ^ "Godot math_defs.h". GitHub.com.
  8. ^ "Godot MathfEx.cs". GitHub.com.
  9. ^ "Kayan Nokta Sayılarının Karşılaştırılması, 2012 Sürümü". randomascii.wordpress.com.
  10. ^ "Java Dili ve Sanal Makine Özellikleri". Java Belgeleri.
  11. ^ John R. Hauser (Mart 1996). "Sayısal Programlarda Kayan Nokta İstisnalarını İşleme" (PDF). Programlama Dilleri ve Sistemlerinde ACM İşlemleri. 18 (2): 139–174. doi:10.1145/227699.227701. S2CID  9820157.
  12. ^ David Stevenson (Mart 1981). "IEEE Görevi P754: İkili kayan nokta aritmetiği için önerilen bir standart". IEEE Bilgisayar. 14 (3): 51–62. doi:10.1109 / C-M.1981.220377.
  13. ^ William Kahan ve John Palmer (1979). "Önerilen bir kayan nokta standardına göre". SIGNUM Haber Bülteni. 14 (Özel): 13–21. doi:10.1145/1057520.1057522. S2CID  16981715.
  14. ^ a b c d "Intel ve Floating-Point - Endüstrinin En Başarılı Standartlarından Birinin Güncellenmesi - Kayan Nokta Standardı için Teknoloji Vizyonu" (PDF). Intel. 2016. Arşivlenen orijinal (PDF) 2016-03-04 tarihinde. Alındı 2016-05-30. (11 sayfa)
  15. ^ a b c d "Kayan Noktadaki Yaşlı Adam ile Bir Röportaj". cs.berkeley.edu. 1998-02-20. Alındı 2016-05-30.
  16. ^ a b Woehr, Jack, ed. (1997-11-01). "William Kahan ile Söyleşi". Dr. Dobb's. drdobbs.com. Alındı 2016-05-30.
  17. ^ W. Kahan 2003, pers. iletişim -e Mike Cowlishaw ve bir IEEE 754 toplantısından sonra diğerleri[güvenilmez kaynak? ]
  18. ^ a b c d "IEEE 754: William Kahan ile Söyleşi" (PDF). dr-chuck.com. Alındı 2016-06-02.
  19. ^ "IEEE ve Microsoft İkili Biçimi; Yuvarlama Sorunları (Tamamlandı)". Microsoft Desteği. Microsoft. 2006-11-21. Makale Kimliği KB35826, Q35826. Arşivlendi 2020-08-28 tarihinde orjinalinden. Alındı 2010-02-24.
  20. ^ Thornton, James E. (1970). Advanced Design Laboratory, Control Data Corporation'da yazılmıştır. Bilgisayar Tasarımı: Kontrol Verileri 6600 (PDF) (1 ed.). Glenview, Illinois, ABD: Scott, Foresman ve Şirket. LCCN  74-96462. Arşivlendi (PDF) 2020-08-28 tarihinde orjinalinden. Alındı 2016-06-02. (1 + 13 + 181 + 2 + 2 sayfa)
  21. ^ Kahan, William Morton. "Neden kayan noktalı aritmetik standardına ihtiyacımız var?" (PDF). cs.berkeley.edu. Alındı 2016-06-02.
  22. ^ Kahan, William Morton; Darcy, Joseph D. "Java'nın Kayan Noktası Her Yerde Herkese Nasıl Zarar Verir" (PDF). cs.berkeley.edu. Alındı 2016-06-02.
  23. ^ Turner, Peter R. (2013-12-21). Sayısal Analiz ve Paralel İşleme: The Lancaster'da verilen dersler .... ISBN  978-3-66239812-8. Alındı 2016-05-30.
  24. ^ "Standart Kayan Nokta Biçimleri için Adlar" (PDF). cs.berkeley.edu. Alındı 2016-06-02.
  25. ^ Charles Kıdem tazminatı (20 Şubat 1998). "Kayan Noktadaki Yaşlı Adam ile Bir Röportaj".
  26. ^ Charles Kıdem tazminatı. "IEEE Kayan Nokta Biçiminin Tarihçesi". Bağlantılar.
  27. ^ "Moleküler İfadeler: Bilim, Optik ve Siz - Olympus MIC-D: Tümleşik Devre Galerisi - Intel 8087 Matematik Yardımcı İşlemcisi". micro.magnet.fsu.edu. Alındı 2016-05-30.
  28. ^ Kahan, William Morton. "İkili Kayan Nokta Aritmetiği için IEEE Standard 754" (PDF). cs.berkeley.edu. Alındı 2016-06-02.

daha fazla okuma

Dış bağlantılar