Lode koordinatları - Lode coordinates

Lode koordinatları veya Haigh-Westergaard koordinatları .[1] bir dizi tensör değişmezleri alanını kapsayan gerçek, simetrik, ikinci dereceden, 3 boyutlu tensörler ve izomorf göre temel gerilim alanı. Bu sağlak dikey koordinat sistemi, orta asal gerilmenin metal plastisite üzerindeki etkisini açıklayan 1926'da yazdığı ufuk açıcı makalesi nedeniyle Alman bilim adamı Dr.Walter Lode'un onuruna adlandırılmıştır.[2] Tensör değişmez kümelerinin diğer örnekleri, temel gerilimler kümesidir. veya kinematik değişmezler kümesi . Lode koordinat sistemi şu şekilde tanımlanabilir: silindirik koordinat sistemi Çakışan bir orijine sahip temel gerilim alanı içinde ve vektöre paralel z ekseni .
Mekanik değişmezler
Lode koordinatları, mekanik kullanılarak en kolay şekilde hesaplanır değişmezler. Bu değişmezler, değişmezlerin bir karışımıdır. Cauchy stres tensörü, , ve stres saptırıcı, ve tarafından verilir[3]
eşdeğer olarak yazılabilir Einstein gösterimi
nerede ... Levi-Civita sembolü (veya permütasyon sembolü) ve son iki form eşdeğerdir çünkü simetriktir ().
Bu değişmezlerin gradyanları[4] tarafından hesaplanabilir
nerede 3x3 kimlik matrisi ve Hill tensörü olarak adlandırılır.
Eksenel koordinat
koordinat, büyüklüğünün hesaplanmasıyla bulunur. dikey projeksiyon stres durumunun üzerine hidrostatik eksen.
nerede
hidrostatik eksen yönündeki normal birimdir.
Radyal koordinat
-Kordinat, gerilim sapıcısının (the dikey projeksiyon gerilme durumunun deviatorik düzlemine).
nerede
Türetme İlişki ilişkiyi genişleterek bulunabilir ve yazı izotropik ve deviatorik parçalar açısından, büyüklüğünü genişletirken
- .
Çünkü izotropik ve deviatoriktir, ürünleri sıfırdır. Bizi bırakan
Kimliği uygulamak ve tanımını kullanarak
radyal bileşen yönünde bir birim tensördür.
Lode açısı - açısal koordinat

Lode açısı, oldukça gevşek bir şekilde, yükleme türünün bir ölçüsü olarak kabul edilebilir. Lode açısı ortaya göre değişir özdeğer stresin. Her biri farklı trigonometrik fonksiyonları kullanan Lode açısının birçok tanımı vardır: pozitif sinüs,[5] negatif sinüs,[6] ve pozitif kosinüs[7] (burada gösterilir , , ve , sırasıyla)
ve ile ilgilidir
Türetme Arasındaki ilişki ve sinüs ve kosinüsü bir kayma ile ilişkilendiren bir trigonometrik kimlik uygulayarak gösterilebilir - .
Çünkü kosinüs bir eşit işlev ve aralığı ters kosinüs genellikle olası negatif değeri alırız bu nedenle, olumlu.
Bu tanımların tümü, bir dizi .
| Stres Durumu | ||||
|---|---|---|---|---|
| Aralık | ||||
| Üç Eksenli Sıkıştırma (TXC) | ||||
| Kesme (SHR) | ||||
| Üç Eksenli Uzatma (TXE) |
Ortonormal temeli tamamlayan açısal yöndeki normal birim şu şekilde hesaplanabilir: [8] ve [9] kullanma
- .
Meridional profil
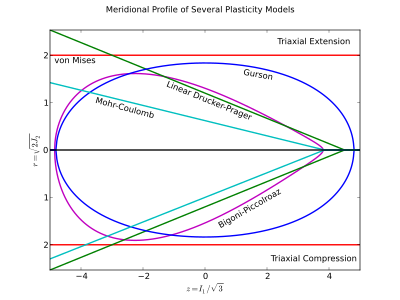
meridyen profil 2D bir çizimdir tutma sabit ve bazen skaler katları kullanılarak çizilir . Yaygın olarak bir basınç bağımlılığını göstermek için kullanılır. akma yüzeyi veya bir gerilim yolunun basınç-kesme yörüngesi. Çünkü dır-dir negatif olmayan arsa genellikle şunun negatif kısmını atlar -eksen, ancak karşıt Lode açılarındaki etkileri göstermek için dahil edilebilir (genellikle üç eksenli uzama ve üç eksenli sıkıştırma).
Meridyen profilini çizmenin faydalarından biri akma yüzeyinin geometrik olarak doğru bir tasviridir.[8] Meridyen profili için izomorfik olmayan bir çift kullanılırsa, akma yüzeyine normal, meridyonel profilde normal görünmeyecektir. Farklı olan herhangi bir koordinat çifti Eşit mutlak değerin sabit katları ile aynı zamanda temel gerilim uzayına göre izomorfiktir. Örnek olarak, baskı ve Von Mises stresi izomorfik bir koordinat çifti değildir ve bu nedenle akma yüzeyini bozar, çünkü
ve sonunda, .
Sekiz yüzlü profil

Oktahedral profil, 2 boyutlu bir çizimdir. tutma sabit. Akma yüzeyinin oktahedral düzlemde çizilmesi, Lode açı bağımlılığının seviyesini gösterir. Oktahedral düzlem bazen 'pi düzlemi' olarak anılır.[10] veya 'deviatorik düzlem'.[11]
Oktahedral profil, farklı basınç değerleri için mutlaka sabit değildir. von Mises getiri kriteri ve Tresca getiri kriteri tüm basınç değerleri için sabittir.
Terminoloji üzerine bir not
Dönem Haigh-Westergaard alanı literatürde, hem Kartezyen asal gerilim uzayını ifade etmek için belirsiz bir şekilde kullanılır[12][13] ve silindirik Lode koordinat alanı[14][15]
Ayrıca bakınız
- Verim (mühendislik)
- Plastisite (fizik)
- Stres
- Henri Tresca
- von Mises stresi
- Mohr-Coulomb teorisi
- Gerginlik
- Gerinim tensörü
- Stres-enerji tensörü
- Stres konsantrasyonu
- 3 boyutlu esneklik
Referanslar
- ^ Menetrey, P.H., Willam, K.J., 1995, Beton İçin Üç Eksenli Hasar Kriteri ve Genellemesi, ACI Structural Journal
- ^ Lode, W. (1926). Versuche über den Einfuss der mittleren Hauptspannung auf das Fliessen der Metalle Eisen Kupfer und Nickel. Zeitung Phys., Cilt. 36, s. 913–939.
- ^ Asaro, R.J., Lubarda, V.A., 2006, Katıların ve Malzemelerin Mekaniği, Cambridge University Press
- ^ Brannon, R.M., 2009, KAYENTA: Teori ve Kullanıcı Kılavuzu, Sandia Ulusal Laboratuvarları, Albuquerque, New Mexico.
- ^ Chakrabarty, J., 2006, Plastisite Teorisi: Üçüncü baskı, Elsevier, Amsterdam.
- ^ de Souza Neto, E.A., Peric, D., Owen, D.R.J., 2008, Plastisite için Hesaplamalı Yöntemler, Wiley
- ^ Han, D.J., Chen, W.F., 1985, Beton Malzemeler için Düzgün Olmayan Sertleşen Plastisite Modeli, Malzemelerin mekaniği
- ^ a b Brannon, R.M., 2007, Fenomenolojik Plastisitenin Unsurları: Geometrik İçgörü, Hesaplamalı Algoritmalar ve Şok Fiziğinde Konular, Şok Dalgası Bilim ve Teknoloji Referans Kitaplığı: Solids I, Springer-New York
- ^ Bigoni, D., Piccolroaz, A., 2004, Yarı kırılgan ve sürtünmeli malzemeler için akma kriterleri, Int. J. Solids Struct.
- ^ Lubliner, J., 1990, Plastisite Teorisi, Pearson Education
- ^ Chaboche, J.L., 2008, Bazı plastisite ve viskoplastisite teorilerinin bir incelemesi, Int. J. Plastisite
- ^ Mouazen, A.M., Nemenyi, M., 1998, Toprak işlemenin sonlu eleman modelleme tekniklerinin gözden geçirilmesi, Simülasyonda Matematik ve Bilgisayarlar
- ^ Keryvin, V., 2008, Metalik camların basınca duyarlılığı için bir prob olarak girinti, J. Phys .: Condens. Önemli olmak
- ^ Cervenka, J., Papanikolaou, V.K., 2008, Beton için üç boyutlu kombine kırılma-plastik malzeme modeli, Int. J. of Plasticity
- ^ Piccolroaz, A., Bigoni, D., 2009, Yarı kırılgan ve sürtünmeli malzemeler için akma kriterleri: Köşeli yüzeylere bir genelleme, Int. J. of Solids and Struc.















![{ displaystyle J_ {2} = { frac {1} {2}} sol [{ text {tr}} ({ boldsymbol { sigma}} ^ {2}) - { frac {1} { 3}} { text {tr}} ({ boldsymbol { sigma}}) ^ {2} right] = { frac {1} {2}} mathrm {tr} left ({ boldsymbol { s}} cdot { boldsymbol {s}} right) = { frac {1} {2}} lVert { boldsymbol {s}} rVert ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e2951ec287d262a6009c66367c0c8f7768bf5b8)


![{ displaystyle J_ {2} = { frac {1} {2}} sol [{ text {tr}} ({ boldsymbol { sigma}} ^ {2}) - { frac {1} { 3}} { text {tr}} ({ boldsymbol { sigma}}) ^ {2} right] = { frac {1} {2}} s_ {ij} s_ {ji} = { frac {1} {2}} s_ {ij} s_ {ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72835af8ac7673b39afc869f9746ca09aa043410)






















































