Küre eversiyonu - Sphere eversion - Wikipedia



İçinde diferansiyel topoloji, küre eversiyonu bir çevirme süreci küre içinde dışarıda üç boyutlu uzay. (Kelime tersine dönme "tersyüz" anlamına gelir.) Dikkat çekici bir şekilde, bir küreyi bu şekilde sorunsuz ve sürekli olarak tersyüz etmek mümkündür (mümkün kendi kendine kesişimler ) kesmeden, yırtmadan veya oluşturmadan buruşmak. Bu, hem matematikçi olmayanlar hem de anlayanlar için şaşırtıcıdır. düzenli homotopi ve bir gerçek paradoks; bu doğru olsa da ilk bakışta yanlış görünen bir şeydir.
Daha doğrusu
standart ol gömme; o zaman bir düzenli homotopi nın-nin daldırmalar
öyle ki ƒ0 = ƒ ve ƒ1 = −ƒ.
Tarih
Bir varoluş kanıtı kırışıksız küre eversiyonu için ilk olarak Stephen Smale (1957 Böyle bir dönüşün belirli bir örneğini görselleştirmek zordur, ancak bazıları dijital animasyonlar bunu biraz daha kolaylaştıran üretildi. İlk örnek, birkaç matematikçinin çabalarıyla sergilendi. Arnold S. Shapiro ve Bernard Morin, kim kördü. Öte yandan, böyle bir "dönüş" ün var olduğunu ve Smale'in yaptığını kanıtlamak çok daha kolay.
Smale'nin mezun danışmanı Raoul Bott Smale'e ilk başta sonucun açıkça yanlış olduğunu söyledi (Levy 1995 ). Onun mantığı şuydu: derece of Gauss haritası böyle bir "dönüşte" korunmalıdır - özellikle de böyle bir dönme nın-nin S1 içinde R2. Ama düğünler için Gauss haritasının dereceleri f ve -f içinde R3 her ikisi de 1'e eşittir ve yanlış tahmin edilebileceği gibi ters işareti yoktur. Tüm daldırmaların Gauss haritasının derecesi S2 içinde R3 1, yani engel yok. "Doğrusal paradoks" terimi, bu düzeyde belki daha uygun bir şekilde geçerlidir: Smale'in çalışmasına kadar, tersine dönme lehine veya aleyhine tartışmak için belgelenmiş bir girişim yoktu. S2ve sonraki çabalar geçmişe bakmaktadır, bu nedenle, kürenin evrimi ile ilişkili tarihsel bir paradoks asla olmadı, yalnızca fikirle ilk kez karşılaşanlar tarafından görselleştirmedeki inceliklerin takdir edilmesi.
Görmek h-prensip daha fazla genelleme için.
Kanıt
Smale'in orijinal kanıtı dolaylıydı: Kürelerin daldırma sınıflarını (düzenli homotopi) bir homotopi grubu ile tanımladı. Stiefel manifoldu. Homotopi grubundan beri içinde kaybolur, standart gömme ve içten dışa doğru düzenli homotopik olmalıdır. Prensipte, açık bir düzenli homotopi üretmek için kanıt çözülebilir, ancak bunu yapmak kolay değildir.
Açık ve güzel örnekler üretmenin birkaç yolu vardır. matematiksel görselleştirme:
- Yarım yol modelleri: bunlar çok özel homotopilerden oluşur. Bu, ilk olarak Shapiro ve Phillips tarafından yapılan orijinal yöntemdir. Çocuğun yüzeyi, daha sonra diğerleri tarafından rafine edildi. Orijinal yarı-yol model homotopileri elle oluşturuldu ve topolojik olarak çalıştı ancak minimum düzeyde değildi. Nelson Max tarafından yedi yıllık bir süre boyunca yaratılan ve Charles Pugh'un tavuk teli modellerine dayanan (daha sonra Berkeley'deki Matematik Bölümünden çalınan) film, o dönem için bir bilgisayar grafiği 'güç gösterisi' idi ve uzun yıllardır bilgisayar animasyonu için kriter. Daha yeni ve kesin bir grafik iyileştirmesi (1980'ler) minimax eversiyonları, hangisi bir değişken yöntem ve özel homotopilerden oluşur (bunlar göre en kısa yollardır. Willmore enerji ). Buna karşılık, Willmore enerjisinin davranışını anlamak, dördüncü dereceden kısmi diferansiyel denklemlerin çözümlerini anlamayı gerektirir ve bu nedenle görsel olarak güzel ve çağrıştıran görüntüler, Smale'in orijinal soyut kanıtının ötesinde bazı çok derin matematikleri yalanlar.
- Thurston dalgaları: bu bir topolojik yöntem ve jenerik; bir homotopi alır ve onu düzensiz bir homotopi olacak şekilde bozar. Bu, bilgisayar grafik animasyonunda gösterilmiştir Dıştan içe geliştirildi Geometri Merkezi Silvio Levy, Delle Maxwell ve Tamara Munzner.[2]
- Aitchison'un 'holiverse' (2010): Bu, topolojik ve geometrik yöntemlerin bir kombinasyonunu kullanır ve standart olarak gömülü 2-küre ile ters yönlendirmeli gömme arasındaki gerçek düzenli homotopi'ye özgüdür. Bu, 3 boyutlu projektif düzlemin somut yapısından ve Hopf fibrasyonunun temel geometrisinden kaynaklandığı ortaya çıkan süreç için kavramsal bir anlayış sağlar. Bu matematiksel kavramların ayrıntılarını anlamak, ortaya çıkan somut evrimi kavramsal olarak değerlendirmek için gerekli değildir; bu, özünde yalnızca 3-uzayda bir simit üzerine çizilen belirli bir gömülü daireyi anlamayı gerektirir. George Francis, "holistik" kelimesinden türetilen "holiverse" adını önerdi, çünkü (biraz düşündükten sonra) tam ters çevirme, animasyonun sağladığı görsel yardımlar olmadan kavramsal olarak baştan sona kavranabilir. Özünde, bu ilk olarak Shapiro tarafından ileri sürülen fikirlere daha yakındır ve pratikte Smale'in ispatının altında yatan soyutlamayı gerektirmeyen somut bir sapma kanıtı sağlar. Bu kısmen bir Povray bilgisayar grafik animasyonu, yine YouTube'da arama yaparak kolayca bulunabilir.
- Yukarıdaki yöntemleri birleştirerek, tam küre eversiyonu, minimum topolojik karmaşıklık veren bir dizi kapalı denklemle tanımlanabilir. [1]
Varyasyonlar
- Altı boyutlu bir küre yedi boyutlu eucledian uzayda tersliği kabul ediyor. Açıkça 0 boyutlu bir küre durumu ile (iki ayrı nokta) gerçek bir çizgide ve yukarıda açıklanan iki boyutlu bir küre durumu küre olduğunda sadece üç durum vardır öklid uzayına gömülü tersliği kabul ediyor.
Eversiyon adımları galerisi
Dört noktalı yarı yol modeli  üstten görünüm  çapraz görünüm  yandan görünüş | Yarısında kapalı  üstten görünüm  çapraz görünüm 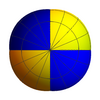 yandan görünüş | Üç noktaların kurallı ölüm modeli  üstten görünüm  çapraz görünüm  yandan görünüş |
Merkezi kesişim döngüsünün kurallı modeli  üstten görünüm  çapraz görünüm  yandan görünüş | Son aşamanın kurallı modeli  üstten görünüm  çapraz görünüm  yandan görünüş | |






Ayrıca bakınız
Referanslar
- ^ a b Bednorz, Adam; Bednorz, Witold (2017). "Minimum topolojik olaylarla analitik küre evrimi". arXiv:1711.10466 [math.GT ].
- ^ "Dışarıdan İçe: Giriş". Geometri Merkezi. Alındı 21 Haziran 2017.
Kaynakça
- Iain R. Aitchison (2010) `` Holiverse ': R ^ 3'teki 2-kürenin bütünsel eversiyonu, ön baskı. arXiv: 1008.0916.
- John B. Etnyre (2004) "geometride h-ilkeleri ve esneklik" in gözden geçirilmesi, BAY1982875.
- Francis, George K. (2007), Topolojik bir resim kitabı, Berlin, New York: Springer-Verlag, ISBN 978-0-387-34542-0, BAY 2265679
- George K. Francis ve Bernard Morin (1980) "Arnold Shapiro'nun Kürenin Evrimi", Matematiksel Zeka 2(4):200–3.
- Levy, Silvio (1995), "Küre eversiyonlarının kısa bir tarihi", Dalga yaratmak, Wellesley, MA: A K Peters Ltd., ISBN 978-1-56881-049-2, BAY 1357900
- Max, Nelson (1977) "Bir Küreyi Tersine Çevirmek", https://www.crcpress.com/Turning-a-Sphere-Inside-Out-DVD/Max/9781466553941
- Anthony Phillips (Mayıs 1966) "Bir yüzeyi tersyüz etmek", Bilimsel amerikalı, s. 112–120.
- Smale, Stephen (1958), "İki kürenin batırılmalarının bir sınıflandırması", Amerikan Matematik Derneği İşlemleri, 90 (2): 281–290, doi:10.2307/1993205, ISSN 0002-9947, JSTOR 1993205, BAY 0104227
Dış bağlantılar
- Dıştan içe, tam video (kısa klip İşte )
- Küre Eversions Tarihi
- "Bir Küreyi Tersine Çevirmek"
- Küre eversiyonunu görselleştirmek için yazılım
- Matematik görselleştirme: topoloji. Holiverse küre eversiyonu (Povray animasyonu)
- DeNeve / Hills küresi evrimi: video ve etkileşimli model
- Patrick Massot'un projesi kanıtı resmileştirmek Yalın Teorem Atasözü
- Bir etkileşimli keşif Adam Bednorz ve Witold Bednorz küre eversiyonu yöntemi











