Ağaç ayrışması - Tree decomposition

İçinde grafik teorisi, bir ağaç ayrışması bir eşlemedir grafik içine ağaç tanımlamak için kullanılabilir ağaç genişliği grafiğe bakın ve grafikteki belirli hesaplama sorunlarını çözmeyi hızlandırın.
Ağaç ayrıştırmaları da denir bağlantı ağaçları, klik ağaçlarıveya ağaçlara katıl; gibi sorunlarda önemli bir rol oynarlar. olasılıksal çıkarım, kısıtlama memnuniyeti, sorgu optimizasyonu,[kaynak belirtilmeli ] ve matris ayrışımı.
Ağaç ayrıştırmaları kavramı ilk olarak Rudolf Halin (1976 ). Daha sonra tarafından yeniden keşfedildi Neil Robertson ve Paul Seymour (1984 ) ve o zamandan beri birçok başka yazar tarafından incelenmiştir.[1]
Tanım
Sezgisel olarak, bir ağaç ayrıştırması, belirli bir grafiğin köşelerini temsil eder. G bir ağacın alt ağaçları olarak, verilen grafikteki köşeler yalnızca karşılık gelen alt ağaçlar kesiştiğinde bitişik olacak şekilde. Böylece, G oluşturur alt grafik of kavşak grafiği alt ağaçların. Tam kesişim grafiği bir akor grafiği.
Her bir alt ağaç, bir dizi ağaç düğümüyle bir grafik tepe noktasını ilişkilendirir. Bunu resmi olarak tanımlamak için, her bir ağaç düğümünü kendisiyle ilişkili tepe noktaları kümesi olarak temsil ederiz. G = (V, E), bir ağaç ayrışması bir çifttir (X, T), nerede X = {X1, ..., Xn} bir alt kümeler ailesidir (bazen çanta) nın-nin V, ve T düğümleri alt kümeler olan bir ağaçtır Xben, aşağıdaki özellikleri karşılamaktadır:[2]
- Tüm setlerin birliği Xben eşittir V. Yani, her grafik tepe noktası en az bir ağaç düğümü ile ilişkilidir.
- Her kenar için (v, w) grafikte bir alt küme var Xben ikisini de içeren v ve w. Diğer bir deyişle, köşeler, yalnızca karşılık gelen alt ağaçların ortak bir düğüme sahip olması durumunda grafikte bitişiktir.
- Eğer Xben ve Xj her ikisi de bir tepe noktası içerir v, sonra tüm düğümler Xk ağacın (benzersiz) yoldaki Xben ve Xj içeren v yanı sıra. Yani, köşe ile ilişkili düğümler v bağlı bir alt kümesini oluşturmak T. Bu aynı zamanda tutarlılık olarak da bilinir veya çalışan kavşak özelliği. Eşdeğer olarak, eğer , ve düğümler ve yol üzerinde -e , sonra .
Bir grafiğin ağaç ayrışımı benzersiz olmaktan uzaktır; örneğin, önemsiz bir ağaç ayrıştırması, grafiğin tüm köşelerini tek kök düğümünde içerir.
Altta yatan ağacın bir ağaç ayrışması yol grafiği yol ayrıştırması olarak adlandırılır ve bu özel ağaç ayrıştırma türlerinden türetilen genişlik parametresi olarak bilinir yol genişliği.
Bir ağaç ayrışması (X, T = (ben, F)) ağaç genişliği k dır-dir pürüzsüzeğer hepsi için ve herkes için .[3]
Bir ağaç ayrışmasındaki minimum ağaç sayısı, ağaç numarası nın-nin G.
Ağaç genişliği
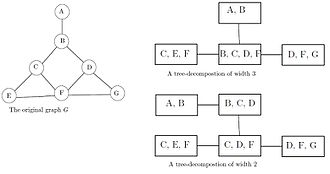
Genişlik bir ağaç ayrışmasının boyutu, en büyük kümesinin boyutudur Xben eksi bir. ağaç genişliği tw (G) bir grafiğin G olası tüm ağaç ayrışımları arasındaki minimum genişliktir. G. Bu tanımda, bir ağacın ağaç genişliğini bire eşit hale getirmek için en büyük kümenin boyutu bir azaltılır. Ağaç genişliği, ağaç ayrıştırmalarından başka yapılardan da tanımlanabilir. akor grafikleri, Brambles, ve Cennetler.
Belirli bir grafiğin G belirli bir değişkende en fazla ağaç genişliğine sahiptir k.[4]Ancak ne zaman k herhangi bir sabit sabittir, ağaç genişliğine sahip grafikler k tanınabilir ve bir genişlik k onlar için doğrusal zamanda inşa edilmiş ağaç ayrışımı.[3] Bu algoritmanın zamana bağlılığı k üsteldir.
Dinamik program
1970'lerin başında, grafiklerde tanımlanan büyük bir kombinatoryal optimizasyon problemleri sınıfının, seri olmayan yöntemlerle verimli bir şekilde çözülebildiği görülmüştür. dinamik program grafik sınırlı olduğu sürece boyut,[5] ağaç genişliğiyle ilgili bir parametre. 1980'lerin sonunda birkaç yazar bağımsız olarak gözlemledi,[6] algoritmik problemler NP tamamlandı keyfi grafikler için verimli bir şekilde çözülebilir: dinamik program Sınırlı ağaç genişliğinin grafikleri için, bu grafiklerin ağaç ayrıştırmalarını kullanarak.
Örnek olarak, maksimum bağımsız küme ağaç genişliği grafiğinde k. Bu sorunu çözmek için, önce ağaç ayrıştırmasının düğümlerinden birini keyfi olarak kök olarak seçin. Bir düğüm için Xben ağacın ayrışmasına izin ver Dben setlerin birliği ol Xj inen Xben. Bağımsız bir set için S ⊂ Xben, İzin Vermek Bir(S,ben) en büyük bağımsız alt kümenin boyutunu belirtir ben nın-nin Dben öyle ki ben ∩ Xben = S. Benzer şekilde, bitişik bir düğüm çifti için Xben ve Xj, ile Xben ağacın kökünden daha uzakta Xjve bağımsız bir küme S ⊂ Xben ∩ Xj, İzin Vermek B(S,ben,j) en büyük bağımsız alt kümenin boyutunu belirtir ben nın-nin Dben öyle ki ben ∩ Xben ∩ Xj = S. Bunları hesaplayabiliriz Bir ve B ağacın aşağıdan yukarıya geçişiyle değerler:
hesaplamadaki toplam nerede düğümün çocuklarının üzerinde .
Her düğümde veya kenarda, en fazla 2k setleri S bunun için bu değerleri hesaplamamız gerekiyor, öyleyse k sabit ise, hesaplamanın tamamı kenar veya düğüm başına sabit zaman alır. Maksimum bağımsız kümenin boyutu, kök düğümde depolanan en büyük değerdir ve maksimum bağımsız kümenin kendisi (dinamik programlama algoritmalarında standart olduğu gibi), bu en büyük değerden başlayarak bu depolanmış değerler üzerinden geriye doğru izleme yoluyla bulunabilir. Böylece, sınırlı ağ genişliğine sahip grafiklerde, maksimum bağımsız küme problemi doğrusal zamanda çözülebilir. Benzer algoritmalar diğer birçok grafik problemi için de geçerlidir.
Bu dinamik programlama yaklaşımı, makine öğrenme aracılığıyla bağlantı ağacı algoritması için inanç yayılımı sınırlı ağaç genişliği grafiklerinde. Aynı zamanda, ağaç genişliğini hesaplamak ve ağaç ayrıştırmaları oluşturmak için algoritmalarda önemli bir rol oynar: tipik olarak, bu tür algoritmalar, yaklaşık ağaç genişliği, bu yaklaşık genişlikte bir ağaç ayrışımı oluşturmak ve ardından ağaç genişliğinin tam değerini hesaplamak için yaklaşık ağaç ayrıştırmasında dinamik programlama gerçekleştiren ikinci bir adım.[3]
Ayrıca bakınız
- Brambles ve Cennetler - Bir grafiğin ağaç genişliğini tanımlamada ağaç ayrıştırmasına alternatif olarak kullanılabilecek iki tür yapı.
- Dal ayrıştırma - Genişliği sabit bir ağaç genişliği faktörü içinde olan yakından ilişkili bir yapı.
- Ayrıştırma Yöntemi - Ayrıştırma Yönteminde kısıtlı tatmin problemini çözmek için Ağaç Ayrıştırma kullanılmıştır.
Notlar
Referanslar
- Arnborg, S .; Corneil, D.; Proskurowski, A. (1987), "Bir yerde düğün bulmanın karmaşıklığı k- ağaç ", Matris Analizi ve Uygulamaları Üzerine SIAM Dergisi, 8 (2): 277–284, doi:10.1137/0608024.
- Arnborg, S .; Proskurowski, A. (1989), "Kısmi sınırlı NP-zor problemler için doğrusal zaman algoritmaları k-ağaçlar ", Ayrık Uygulamalı Matematik, 23 (1): 11–24, doi:10.1016 / 0166-218X (89) 90031-0.
- Bern, M. W .; Lawler, E.L.; Wong, A. L. (1987), "Ayrıştırılabilir grafiklerin optimal alt grafiklerinin doğrusal zaman hesaplaması", Algoritmalar Dergisi, 8 (2): 216–235, doi:10.1016/0196-6774(87)90039-3.
- Bertelé, Umberto; Brioschi, Francesco (1972), Seri Olmayan Dinamik ProgramlamaAkademik Basın, ISBN 0-12-093450-7.
- Bodlaender, Hans L. (1988), "Sınırlı ağaç genişliğine sahip grafiklerde dinamik programlama", Proc. Otomata, Diller ve Programlama Konulu 15. Uluslararası Kolokyum, Bilgisayar Bilimleri Ders Notları, 317, Springer-Verlag, s. 105–118, doi:10.1007/3-540-19488-6_110.
- Bodlaender, Hans L. (1996), "Küçük ağaç genişliğinin ağaç ayrışımlarını bulmak için doğrusal bir zaman algoritması", Bilgi İşlem Üzerine SIAM Dergisi, 25 (6): 1305–1317, CiteSeerX 10.1.1.113.4539, doi:10.1137 / S0097539793251219.
- Diestel Reinhard (2005), Grafik teorisi (3. baskı), Springer, ISBN 3-540-26182-6.
- Halin, Rudolf (1976), "S- grafikler için işlevler ", Geometri Dergisi, 8: 171–186, doi:10.1007 / BF01917434.
- Robertson, Neil; Seymour, Paul D. (1984), "Grafik küçükler III: Düzlemsel ağaç genişliği", Kombinatoryal Teori Dergisi, B Serisi, 36 (1): 49–64, doi:10.1016/0095-8956(84)90013-3.









