Nelder – Mead yöntemi - Nelder–Mead method
 | |
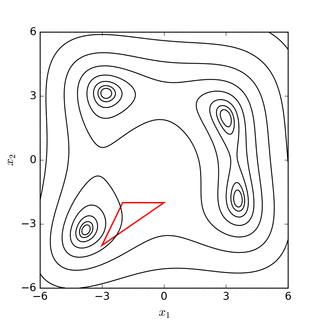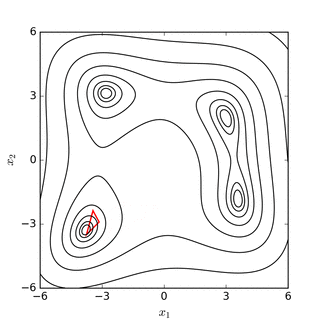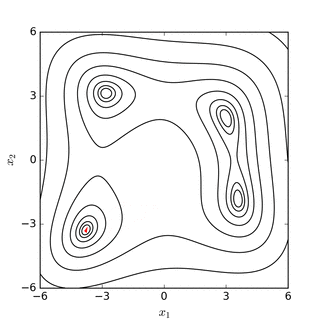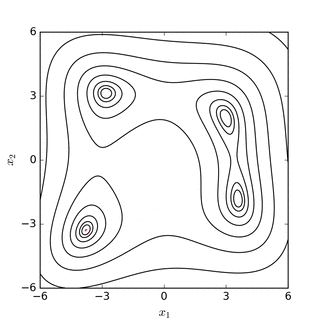 Nelder – Mead simpleks arama Rosenbrock muz işlevi(yukarıda) ve Himmelblau'nun işlevi (altında) |

Nelder – Mead yöntemi (Ayrıca yokuş aşağı simpleks yöntemi, amip yöntemiveya politop yöntemi) yaygın olarak uygulanan bir Sayısal yöntem minimum veya maksimum bir değeri bulmak için kullanılır amaç fonksiyonu çok boyutlu bir uzayda. Bu bir doğrudan arama yöntemi (fonksiyon karşılaştırmasına dayanır) ve genellikle doğrusal olmayan optimizasyon türevlerinin bilinemeyebileceği sorunlar. Bununla birlikte, Nelder – Mead tekniği bir sezgisel sabit olmayan noktalara yakınlaşabilen arama yöntemi[1] alternatif yöntemlerle çözülebilecek sorunlar üzerinde.[2]
Nelder-Mead tekniği, John Nelder ve Roger Mead 1965'te[3] Spendley ve ark yönteminin bir gelişimi olarak.[4]
Genel Bakış
Yöntem, bir kavramını kullanır basit özel olan politop nın-nin n İçinde + 1 köşe n boyutlar. Basitlik örnekleri arasında bir çizgi üzerindeki bir çizgi parçası, bir düzlemdeki bir üçgen, bir dörtyüzlü üç boyutlu uzayda vb.
Yöntem, bir problemin yerel optimumuna yaklaşır. n amaç işlevi sorunsuz bir şekilde değiştiğinde ve tek modlu. Tipik uygulamalar işlevleri en aza indirir ve en üst düzeye çıkarırız küçülterek .
Örneğin, bir asma köprü mühendisinin her bir dikme, kablo ve ayağın ne kadar kalın olması gerektiğini seçmesi gerekir. Bu unsurlar birbirine bağlıdır, ancak belirli bir unsuru değiştirmenin etkisini görselleştirmek kolay değildir. Bu tür karmaşık yapıların simülasyonunun çalıştırılması genellikle hesaplama açısından son derece pahalıdır ve muhtemelen yürütme başına saatlerce sürebilir. Nelder – Mead yöntemi, orijinal varyantta, yineleme başına en fazla iki değerlendirme gerektirir; küçültmek diğer bazı doğrudan arama optimizasyon yöntemlerine kıyasla çekici olan işlem daha sonra açıklanacaktır. Bununla birlikte, önerilen optimum için toplam iterasyon sayısı yüksek olabilir.
Nelder – Mead n boyutlar bir dizi korur n + 1 test noktası olarak düzenlenmiş basit. Daha sonra yeni bir test noktası bulmak ve eski test noktalarından birini yenisiyle değiştirmek için her test noktasında ölçülen objektif fonksiyonun davranışını tahmin eder ve böylece teknik ilerler. En basit yaklaşım, en kötü noktayı, üzerinden yansıtılan bir noktayla değiştirmektir. centroid kalan n puan. Bu nokta mevcut en iyi noktadan daha iyiyse, o zaman bu çizgi boyunca üstel olarak uzatmayı deneyebiliriz. Öte yandan, bu yeni nokta bir önceki değerden çok daha iyi değilse, o zaman bir vadinin üzerinden geçiyoruz, bu yüzden simpleksi daha iyi bir noktaya doğru küçültürüz. Algoritmanın "Sayısal Tarifler" den sezgisel bir açıklaması:[5]
Yokuş aşağı simpleks yöntemi artık bir dizi adım atıyor; çoğu adım, simpleksin en büyük olduğu noktayı ("en yüksek nokta") simpleksin karşı yüzünden daha düşük bir noktaya hareket ettiriyor. Bu adımlar yansımalar olarak adlandırılır ve simpleksin hacmini korumak (ve dolayısıyla dejenerasyonunu sürdürmek) için oluşturulmuştur. Bunu yapabildiğinde, yöntem daha büyük adımlar atmak için simpleksi bir veya başka yönde genişletir. Bir "vadi tabanına" ulaştığında, yöntem enine yönde daralır ve vadiden aşağı sızmaya çalışır. Eğer simpleksin “iğne deliğinden geçmeye” çalıştığı bir durum varsa, kendisini her yöne daraltır ve kendisini en alt (en iyi) noktasından çeker.
Modern optimizasyon yöntemlerinden farklı olarak, Nelder – Mead buluşsal yöntemi, problem modern yöntemler için gerekli olandan daha güçlü koşulları karşılamadığı sürece durağan olmayan bir noktaya yakınsayabilir.[1] Nelder – Mead buluşsal yöntemine göre modern gelişmeler 1979'dan beri bilinmektedir.[2]
Çözülen sorunun gerçek doğasına bağlı olarak birçok varyasyon mevcuttur. Yaygın bir varyant, gradyan yönünü kabaca takip eden sabit boyutlu, küçük bir simpleks kullanır ( en dik iniş ). Bir vadiden aşağıya yerel bir dibe doğru hızla ilerlerken bir yükseklik haritasında küçük bir üçgeni görselleştirin. Bu yöntem aynı zamanda esnek polihedron yöntemi. Bununla birlikte, bu, bu makalede açıklanan yönteme karşı kötü performans gösterme eğilimindedir, çünkü çok az ilgi alanına giren alanlarda küçük, gereksiz adımlar atar.
NM algoritmasının olası bir varyasyonu
(Bu, orijinal Nelder – Mead makalesindeki prosedüre yaklaşmaktadır.)

İşlevi en aza indirmeye çalışıyoruz , nerede . Mevcut test noktalarımız .
1. Sipariş köşelerdeki değerlere göre:
- Yöntemin durması gerekip gerekmediğini kontrol edin. Görmek Sonlandırma altında. Bazen uygunsuz bir şekilde "yakınsama" olarak adlandırılır.
2. Hesaplamak , centroid hariç tüm noktaların .
3. Düşünme
- Yansıyan noktayı hesapla ile .
- Yansıyan nokta en kötü ikinci noktadan daha iyiyse, ancak en iyiden daha iyi değilse, yani. ,
- sonra en kötü noktayı değiştirerek yeni bir simpleks elde edin yansıyan nokta ile ve 1. adıma gidin.
4. Genişletme
- Yansıyan nokta şu ana kadarki en iyi nokta ise, ,
- sonra genişletilmiş noktayı hesaplayın ile .
- Genişletilmiş nokta, yansıtılan noktadan daha iyiyse, ,
- sonra en kötü noktayı değiştirerek yeni bir simpleks elde edin genişletilmiş nokta ile ve 1. adıma gidin;
- yoksa en kötü noktayı değiştirerek yeni bir simpleks elde edin yansıyan nokta ile ve 1. adıma gidin.
5. Kasılma
- İşte kesin ki . (Bunu not et en yüksek ikinci veya "sonraki" dir.)
- Sözleşmeli noktayı hesapla ile .
- Daralan nokta en kötü noktadan daha iyiyse, yani ,
- sonra en kötü noktayı değiştirerek yeni bir simpleks elde edin sözleşmeli nokta ile ve 1. adıma gidin;
6. Küçült
- En iyisi dışındaki tüm noktaları değiştirin () ile
- ve 1. adıma gidin.
Not: , , ve sırasıyla yansıma, genleşme, daralma ve küçülme katsayılarıdır. Standart değerler , , ve .
İçin yansıma, dan beri köşeler arasında ilişkili değeri daha yüksek olan tepe noktasıdır, yansımasında daha düşük bir değer bulmayı bekleyebiliriz tüm köşelerin oluşturduğu karşıt yüzde dışında .
İçin genişleme, eğer yansıma noktası köşeler boyunca yeni minimum değerdir, yön boyunca ilginç değerler bulmayı bekleyebiliriz -e .
İle ilgili olarak kasılma, Eğer , tüm köşelerin oluşturduğu simpleksin içinde daha iyi bir değer olmasını bekleyebiliriz .
Son olarak küçültmek En büyük noktadan uzaklaşmanın arttığı ender durumu ele alır , tekil olmayan bir minimuma yeterince yakın olamayacak bir şey. Bu durumda, daha basit bir manzara bulma beklentisiyle en düşük noktaya doğru daralırız. Ancak Nash, sonlu kesinlikli aritmetiğin bazen simpleksi küçültmede başarısız olabileceğini not eder ve boyutun gerçekte küçültüldüğünü kontrol eder.[6]
İlk simpleks
İlk simpleks önemlidir. Aslında, çok küçük bir ilk simpleks yerel bir aramaya yol açabilir, dolayısıyla NM daha kolay takılıp kalabilir. Dolayısıyla bu simpleks sorunun doğasına bağlı olmalıdır. Bununla birlikte, orijinal makale bir başlangıç noktasının şu şekilde verildiği bir simpleks önerdi , diğerleri sırayla her boyut boyunca sabit bir adımla oluşturulur. Bu nedenle yöntem, oluşturan değişkenlerin ölçeklenmesine duyarlıdır. .
Sonlandırma
Yinelemeli döngüyü kırmak için kriterlere ihtiyaç vardır. Nelder ve Mead, mevcut simpleksin fonksiyon değerlerinin örnek standart sapmasını kullandı. Bunlar bir miktar toleransın altına düşerse, döngü durdurulur ve simpleksteki en düşük nokta önerilen optimum olarak döndürülür. Çok "düz" bir işlevin, büyük bir etki alanında hemen hemen eşit işlev değerlerine sahip olabileceğine dikkat edin, böylece çözüm toleransa duyarlı olacaktır. Nash, başka bir sonlandırma kriteri olarak küçülme testini ekliyor.[6] Yinelemelerin birleşebileceğini, programların sona ereceğini unutmayın.
Ayrıca bakınız
Referanslar
- ^ a b
- Powell, Michael J. D. (1973). "Minimizasyon Algoritmaları için Arama Talimatları". Matematiksel Programlama. 4: 193–201. doi:10.1007 / bf01584660. S2CID 45909653.
- McKinnon, K. I. M. (1999). "Nelder-Mead simpleks yönteminin durağan olmayan bir noktaya yakınsaması". SIAM Optimizasyon Dergisi. 9: 148–158. CiteSeerX 10.1.1.52.3900. doi:10.1137 / S1052623496303482. (algoritma özeti çevrimiçi).
- ^ a b
- Yu, Wen Ci. 1979. "Pozitif temel ve bir doğrudan arama teknikleri sınıfı". Scientia Sinica [Zhongguo Kexue]: 53—68.
- Yu, Wen Ci. 1979. "Simpleks evrim tekniğinin yakınsak özelliği". Scientia Sinica [Zhongguo Kexue]: 69–77.
- Kolda, Tamara G.; Lewis, Robert Michael; Torczon, Virginia (2003). "Doğrudan aramayla optimizasyon: bazı klasik ve modern yöntemlere ilişkin yeni perspektifler". SIAM Rev. 45 (3): 385–482. CiteSeerX 10.1.1.96.8672. doi:10.1137 / S003614450242889.
- Lewis, Robert Michael; Shepherd, Anne; Torczon, Virjinya (2007). "Doğrusal olarak sınırlandırılmış en aza indirgeme için üretim kümesi arama yöntemlerinin uygulanması". SIAM J. Sci. Bilgisayar. 29 (6): 2507–2530. CiteSeerX 10.1.1.62.8771. doi:10.1137/050635432.
- ^ Nelder, John A .; R. Mead (1965). "Fonksiyon minimizasyonu için tek yönlü bir yöntem". Bilgisayar Dergisi. 7 (4): 308–313. doi:10.1093 / comjnl / 7.4.308.
- ^ Spendley, W .; Hext, G.R .; Himsworth, F.R. (1962). "Simpleks Tasarımların Optimizasyon ve Evrimsel İşlemde Sıralı Uygulaması". Teknometri. 4 (4): 441–461. doi:10.1080/00401706.1962.10490033.
- ^
- Basın, W. H .; Teukolsky, S. A .; Vetterling, W. T .; Flannery, B.P. (2007). "Bölüm 10.5. Çok Boyutlarda Yokuş Aşağı Tek Yön Yöntemi". Sayısal Tarifler: Bilimsel Hesaplama Sanatı (3. baskı). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- ^ a b Nash, J.C. (1979). Kompakt Sayısal Yöntemler: Doğrusal Cebir ve Fonksiyon Minimizasyonu. Bristol: Adam Hilger. ISBN 978-0-85274-330-0.
daha fazla okuma
- Avriel, Mordecai (2003). Doğrusal Olmayan Programlama: Analiz ve Yöntemler. Dover Yayıncılık. ISBN 978-0-486-43227-4.
- Coope, I. D .; Price, C.J. (2002). "Sayısal Optimizasyonda Pozitif Tabanlar". Hesaplamalı Optimizasyon ve Uygulamalar. 21 (2): 169–176. doi:10.1023 / A: 1013760716801. S2CID 15947440.
- Gill, Philip E .; Murray, Walter; Wright, Margaret H. (1981). "Çok Değişkenli Düzgün Olmayan Fonksiyonlar için Yöntemler". Pratik Optimizasyon. New York: Akademik Basın. pp.93 –96. ISBN 978-0-12-283950-4.
- Kowalik, J .; Osborne, M.R. (1968). Kısıtlanmamış Optimizasyon Problemleri İçin Yöntemler. New York: Elsevier. pp.24–27. ISBN 0-444-00041-0.
- Swann, W.H. (1972). "Doğrudan Arama Yöntemleri". Murray, W. (ed.). Kısıtlamasız Optimizasyon için Sayısal Yöntemler. New York: Akademik Basın. sayfa 13–28. ISBN 978-0-12-512250-4.
Dış bağlantılar
- Nelder – Mead (Downhill Simplex) açıklaması ve Rosenbrock muz işlevi ile görselleştirme
- John Burkardt: Matlab'da Nelder – Mead kodu - Nelder – Mead yönteminin bir varyasyonunun aynı zamanda Matlab fonksiyonu fminsearch tarafından da uygulandığına dikkat edin.
- SciPy kitaplığında Python'da Nelder-Mead optimizasyonu.
- Nelder-mead - Nelder – Mead yönteminin bir Python uygulaması
- SOVA 1.0 (ücretsiz) - Çeşitli Uygulamalar için Tek Yönlü Optimizasyon
- [1] - HillStormer, doğrusal olmayan, çok değişkenli ve doğrusal kısıtlı Tek Yönlü Optimizasyon için Nelder Mead'in sunduğu pratik bir araçtır.





































