Frank-Wolfe algoritması - Frank–Wolfe algorithm

Frank-Wolfe algoritması bir yinelemeli birinci derece optimizasyon algoritma için kısıtlı dışbükey optimizasyon. Olarak da bilinir koşullu gradyan yöntemi,^[1] azaltılmış gradyan algoritması ve dışbükey kombinasyon algoritmasıyöntem başlangıçta tarafından önerildi Marguerite Frank ve Philip Wolfe 1956'da.^[2] Her yinelemede, Frank – Wolfe algoritması bir Doğrusal yaklaşım ve bu doğrusal işlevin bir küçültücüsüne doğru hareket eder (aynı etki alanını ele geçirir).

Sorun bildirimi

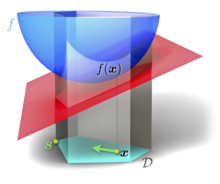
Varsayalım ${ displaystyle { mathcal {D}}}$ bir kompakt dışbükey küme içinde vektör alanı ve ${ displaystyle f iki nokta üst üste { mathcal {D}} - mathbb {R}}$ bir dışbükey, ayırt edilebilir gerçek değerli işlev. Frank-Wolfe algoritması, optimizasyon sorunu

küçültmek ${ displaystyle f ( mathbf {x})}$

tabi ${ mathcal {D}}} içinde { displaystyle mathbf {x}$.

Algoritma

Frank – Wolfe algoritmasının bir adımı

Başlatma: İzin Vermek ${ displaystyle k leftarrow 0}$ve izin ver ${ displaystyle mathbf {x} _ {0} !}$ herhangi bir nokta olmak ${ displaystyle { mathcal {D}}}$.

Aşama 1. Yön bulma alt problemi: Bul ${ displaystyle mathbf {s} _ {k}}$ çözme

küçültmek ${ displaystyle mathbf {s} ^ {T} nabla f ( mathbf {x} _ {k})}$

Tabi ${ mathcal {D}}} içinde { displaystyle mathbf {s}$

(Yorum: Birinci dereceden tarafından verilen problemin doğrusal yaklaşımını en aza indirin Taylor yaklaşımı nın-nin ${ displaystyle f}$ etrafında ${ displaystyle mathbf {x} _ {k} !}$.)

Adım 2. Adım boyutu belirleme: Ayarlamak ${ displaystyle gamma leftarrow { frac {2} {k + 2}}}$veya alternatif olarak bul ${ displaystyle gamma}$ en aza indiren ${ displaystyle f ( mathbf {x} _ {k} + gamma ( mathbf {s} _ {k} - mathbf {x} _ {k}))}$ tabi ${ displaystyle 0 leq gamma leq 1}$ .

Aşama 3. Güncelleme: İzin Vermek ${ displaystyle mathbf {x} _ {k + 1} leftarrow mathbf {x} _ {k} + gamma ( mathbf {s} _ {k} - mathbf {x} _ {k})}$, İzin Vermek ${ displaystyle k leftarrow k + 1}$ ve Adım 1'e gidin.

Özellikleri

Rakip yöntemler gibi dereceli alçalma kısıtlı optimizasyon için bir projeksiyon adımı Her yinelemedeki uygulanabilir kümeye geri döndüğümüzde, Frank-Wolfe algoritması yalnızca her yinelemede aynı küme üzerinde doğrusal bir problemin çözümüne ihtiyaç duyar ve otomatik olarak uygun kümede kalır.

Frank-Wolfe algoritmasının yakınsaması genel olarak alt doğrusaldır: amaç fonksiyonundaki hata optimuma ${ displaystyle O (1 / k)}$ sonra k gradyan olduğu sürece yinelemeler Sürekli Lipschitz bazı normlara göre. Aynı yakınsama oranı, alt problemler sadece yaklaşık olarak çözülürse de gösterilebilir.^[3]

Algoritmanın yinelemeleri her zaman uygulanabilir kümenin en uç noktalarının seyrek bir dışbükey kombinasyonu olarak temsil edilebilir; bu, algoritmanın popülerlikteki seyrek açgözlü optimizasyonuna yardımcı olmuştur. makine öğrenme ve sinyal işleme sorunlar^[4] yanı sıra örneğin optimizasyonu minimum maliyetli akışlar içinde ulaşım ağları.^[5]

Uygulanabilir küme bir dizi doğrusal kısıtlama ile verilmişse, o zaman her yinelemede çözülecek alt problem bir doğrusal program.

En kötü durum yakınsama oranı ile ${ displaystyle O (1 / k)}$ genel olarak iyileştirilemez, bazı güçlü dışbükey problemler gibi özel problem sınıfları için daha hızlı yakınsama elde edilebilir.^[6]

Çözüm değerinde alt sınırlar ve ilkel ikili analiz

Dan beri ${ displaystyle f}$ dır-dir dışbükey herhangi iki nokta için ${ mathcal {D}}} içinde { displaystyle mathbf {x}, mathbf {y}$ sahibiz:

${ displaystyle f ( mathbf {y}) geq f ( mathbf {x}) + ( mathbf {y} - mathbf {x}) ^ {T} nabla f ( mathbf {x})}$

Bu aynı zamanda (bilinmeyen) optimal çözüm için de geçerlidir ${ displaystyle mathbf {x} ^ {*}}$. Yani, ${ displaystyle f ( mathbf {x} ^ {*}) geq f ( mathbf {x}) + ( mathbf {x} ^ {*} - mathbf {x}) ^ {T} nabla f ( mathbf {x})}$. Belirli bir noktaya göre en iyi alt sınır ${ displaystyle mathbf {x}}$ tarafından verilir

${ displaystyle { başlar {hizalı} f ( mathbf {x} ^ {*}) & geq f ( mathbf {x}) + ( mathbf {x} ^ {*} - mathbf {x}) ^ {T} nabla f ( mathbf {x}) & geq min _ { mathbf {y} in D} left {f ( mathbf {x}) + ( mathbf {y } - mathbf {x}) ^ {T} nabla f ( mathbf {x}) right } & = f ( mathbf {x}) - mathbf {x} ^ {T} nabla f ( mathbf {x}) + min _ { mathbf {y} in D} mathbf {y} ^ {T} nabla f ( mathbf {x}) end {hizalı}}}$

İkinci optimizasyon problemi, Frank-Wolfe algoritmasının her yinelemesinde çözülür, dolayısıyla çözüm ${ displaystyle mathbf {s} _ {k}}$ yön bulma alt probleminin ${ displaystyle k}$-th iterasyon artan alt sınırları belirlemek için kullanılabilir ${ displaystyle l_ {k}}$ her yineleme sırasında ayarlayarak ${ displaystyle l_ {0} = - infty}$ ve

${ displaystyle l_ {k}: = max (l_ {k-1}, f ( mathbf {x} _ {k}) + ( mathbf {s} _ {k} - mathbf {x} _ { k}) ^ {T} nabla f ( mathbf {x} _ {k}))}$

Bilinmeyen optimal değerin bu tür alt sınırları pratikte önemlidir, çünkü durdurma kriteri olarak kullanılabilirler ve her yinelemede her yinelemede etkin bir yaklaşım kalitesi sertifikası verirler, çünkü her zaman ${ displaystyle l_ {k} leq f ( mathbf {x} ^ {*}) leq f ( mathbf {x} _ {k})}$.

Bunun karşılık geldiği gösterilmiştir dualite boşluğu, arasındaki fark bu ${ displaystyle f ( mathbf {x} _ {k})}$ ve alt sınır ${ displaystyle l_ {k}}$, aynı yakınsama oranıyla azalır, yani${ displaystyle f ( mathbf {x} _ {k}) - l_ {k} = O (1 / k).}$

Notlar

Kaynakça

• Jaggi Martin (2013). "Frank – Wolfe'u Yeniden Ziyaret Etme: Projeksiyonsuz Seyrek Konveks Optimizasyonu". Makine Öğrenimi Araştırmaları Dergisi: Çalıştay ve Konferans Bildirileri. 28 (1): 427–435. (Genel bakış kağıdı)
• Frank-Wolfe algoritması açıklama
• Nocedal, Jorge; Wright, Stephen J. (2006). Sayısal Optimizasyon (2. baskı). Berlin, New York: Springer-Verlag. ISBN  978-0-387-30303-1.CS1 bakimi: ref = harv (bağlantı).

Dış bağlantılar

• Marguerite Frank, algoritmanın tarihi hakkında kişisel bir açıklama yapıyor

Ayrıca bakınız

• Proksimal gradyan yöntemleri