Periyodik seyahat dalgası - Periodic travelling wave

Kuantum mekaniğinde görülen bir dalga patlaması için bkz. Dalga paketi.
Periyodik hareket eden dalganın şematik gösterimi
Periyodik bir seyahat dalgası

Matematikte bir periyodik seyahat dalgası (veya dalga) bir periyodik fonksiyon bir-boyutlu Uzay sabit hızla hareket eden. Sonuç olarak, özel bir uzay-zamansal salınım bu hem uzayın hem de zamanın periyodik bir fonksiyonudur.

Periyodik hareket eden dalgalar birçok matematiksel denklemde temel bir rol oynar. kendinden salınımlı sistemler,[1][2] uyarılabilir sistemler[3] vereaksiyon-difüzyon-öneri sistemleri.[4] Bu türdeki denklemler yaygın olarak şu şekilde kullanılmaktadır: Matematiksel modeller biyoloji, kimya ve fizik ve periyodik hareket eden dalgalara benzeyen fenomenlerde birçok örnek bulundu. deneysel olarak.

Periyodik hareket eden dalgaların matematiksel teorisi en çok aşağıdakiler için geliştirilmiştir: kısmi diferansiyel denklemler, ancak bu çözümler, integral farklı denklemler de dahil olmak üzere bir dizi başka matematiksel sistemde de ortaya çıkar,[5][6] integrodiffer denklemleri,[7]birleşik harita kafesleri[8]ve hücresel otomata[9][10]

Periyodik hareket eden dalgalar, kendi başlarına önemli olmasının yanı sıra, tek boyutlu eşdeğeri olarak önemlidir. sarmal dalgalar ve iki boyutlu uzayda hedef desenler ve üç boyutlu uzayda kaydırma dalgaları.

Araştırma tarihi

Periyodik gezici dalgalar ilk olarak 1970'lerde çalışıldı. Önemli bir erken araştırma makalesi, Nancy Kopell ve Lou Howard[1] periyodik hareket eden dalgalar üzerinde birkaç temel sonuç olduğunu kanıtladı. reaksiyon-difüzyon denklemleri. Bunu 1970'lerde ve 1980'lerin başlarında önemli araştırma faaliyeti izledi. Daha sonra, periyodik seyahat dalgalarına olan ilgi, nesilleri üzerindeki matematiksel çalışmalarla yenilenmeden önce, bir hareketsizlik dönemi vardı.[11][12] ve onların tespiti ile ekoloji, döngüsel popülasyonlar üzerine uzay-zamansal veri setlerinde.[13][14] 2000'lerin ortalarından beri, periyodik seyahat dalgaları üzerine yapılan araştırmalar, dalgaları incelemek için yeni hesaplama yöntemlerinden yararlandı. istikrar ve mutlak istikrar.[15][16]

Aileler

Periyodik hareket eden dalgaların varlığı genellikle parametre matematiksel bir denklemdeki değerler. Periyodik bir hareket eden dalga çözümü varsa, o zaman tipik olarak farklı dalga hızlarına sahip bu tür bir çözüm ailesi vardır. Kısmi diferansiyel denklemler için, periyodik hareket dalgaları tipik olarak sürekli bir dalga hızı aralığı için meydana gelir.[1]

istikrar

Önemli bir soru, periyodik bir seyahat dalgasının olup olmadığıdır. kararlı veya kararsız orijinal matematiksel sistemin bir çözümü olarak. Kısmi diferansiyel denklemler için, dalga ailesinin alt bölümlere ayrılması tipiktir. kararlı ve kararsız parçalar.[1][17][18] Kararsız periyodik hareket eden dalgalar için önemli bir yardımcı soru, bunların tamamen mi yoksa konvektif olarak kararsız olup olmadıklarıdır, yani durağan büyüyen doğrusal modlar var mıdır?[19] Bu sorun yalnızca birkaç kısmi diferansiyel denklem için çözülmüştür.[2][15][16]

Nesil

Periyodik ilerleyen dalga oluşumunun bir dizi mekanizması artık iyi bir şekilde oluşturulmuştur. Bunlar şunları içerir:

  • Heterojenlik: Parametre değerlerindeki uzaysal gürültü bir dizi periyodik hareket eden dalga oluşturabilir.[20] Bu, salınımlı kimyasal reaksiyonlar kirliliklerin, periyodik hareket eden dalgaların iki boyutlu genelleştirmeleri olan hedef modellere veya spiral dalgalara neden olabileceği yerlerde. Bu süreç, 1970'lerde ve 1980'lerin başlarında periyodik seyahat dalgaları üzerine yapılan çalışmaların çoğu için motivasyon sağladı. Peyzaj heterojenliği, ekolojide görülen periyodik hareket eden dalgaların bir nedeni olarak da öne sürülmüştür.[21]
  • İstilalar, arkalarında periyodik bir yolculuk dalgası bırakabilir.[11][12][22] Bu, Taylor – Couette sistem geçişi varlığında,[23] gibi kimyasal sistemlerde Belousov-Zhabotinsky reaksiyonu[24][25] ve yırtıcı hayvan sistemler ekoloji.[26][27]
  • Dirichlet sınır koşulu tarafından üretilen dalgalar
    Merkezi bir delikte bir Dirichlet sınır koşulu tarafından üretilen dalgalar
    Etki alanı sınırları ile Dirichlet veya Robin sınır şartları.[28][29][30] Bu potansiyel olarak önemlidir ekoloji Robin veya Dirichlet koşullarının, habitat ile çevredeki düşmanca ortam arasındaki sınıra karşılık geldiği yer. Ancak kesin ampirik kanıtlar Ekolojik sistemler için dalgaların nedenini bulmak zordur.
  • Göç takip ve kaçınma.[31] Bu önemli olabilir ekoloji.
  • Alt popülasyonlar arası göç,[32] yine potansiyeli olan ekolojik önemi.

Tüm bu durumlarda, önemli bir soru, periyodik gezici dalga ailesinin hangi üyesinin seçildiğidir. Çoğu matematiksel sistem için bu açık bir problem olarak kalır.

Uzay-zamansal kaos

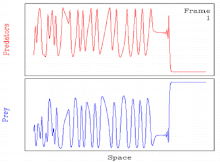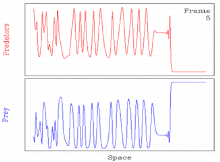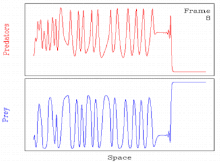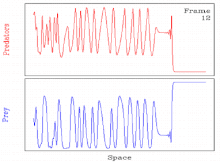
Avcılar tarafından avın simüle edilmiş istilasında periyodik hareket eden dalgalar ve kaos

Bazıları için yaygındır parametre değerleri, bir dalga oluşturma mekanizmasından kaynaklanan periyodik hareket dalgaları kararsızdır. Bu gibi durumlarda çözüm genellikle zamansal uzamsal kaos.[11][27] Bu nedenle çözüm, periyodik hareket eden dalga aracılığıyla uzaysal-zamansal bir kaosa geçişi içerir.

Lambda-omega sistemleri ve karmaşık Ginzburg-Landau denklemi

Periyodik hareket eden dalgalar için prototip görevi gören ve matematiksel anlayış ve teorinin gelişimi için temel olan iki belirli matematiksel sistem vardır. Bunlar "lambda-omega" sınıfıdır. reaksiyon-difüzyon denklemleri[1]

(r=(sen2+v2)1/2) ve karmaşık Ginzburg – Landau denklem.[2]

(Bir karmaşık değerlidir). Bu sistemlerin λ (r)=1-r2, ω (r)=-c r2 ve b= 0. Her iki sistem de denklemlerin genlik açısından yeniden yazılmasıyla basitleştirilebilir (r veya |Bir|) ve faz (arktan (v/sen) veya arg Bir). Denklemler bu şekilde yeniden yazıldıktan sonra, sabit genliğe sahip çözümlerin periyodik hareket eden dalgalar olduğunu ve fazın doğrusal bir fonksiyonu olduğunu görmek kolaydır. Uzay ve zaman. Bu nedenle, sen ve vveya Re (Bir) ve ben(Bir), vardır sinüzoidal uzay ve zamanın işlevleri.

Periyodik gezici dalga aileleri için bu kesin çözümler, çok sayıda ileri analitik çalışmayı mümkün kılar. İçin kesin koşullar istikrar periyodik hareket eden dalgaların bulunabilirliği,[1][2] ve mutlak istikrar koşulu, basit bir çözüme indirgenebilir. polinom.[15][16] Ayrıca istilaların oluşturduğu dalgaların seçim problemi için kesin çözümler elde edilmiştir.[22][33] ve sıfır Dirichlet sınır koşulları ile.[34][35] İkinci durumda, karmaşık Ginzburg-Landau denklemi için genel çözüm sabit bir Nozaki-Bekki deliğidir.[34][36]

Ginzburg-Landau kompleksi içindeki periyodik hareket eden dalgalar üzerine yapılan çalışmaların çoğu, fizik genellikle olarak bilinen edebiyat uçak dalgaları.

Periyodik hareket eden dalgaların sayısal hesaplaması ve kararlılığı

Çoğu matematiksel denklem için, analitik periyodik hareket eden dalga çözümlerinin hesaplanması mümkün değildir ve bu nedenle gerçekleştirmek gereklidir. sayısal hesaplamalar. İçin kısmi diferansiyel denklemler ile belirtmek x ve t (tek boyutlu) Uzay ve zaman değişkenleri sırasıyla. Daha sonra periyodik hareket eden dalgalar, hareket eden dalga değişkeninin fonksiyonudur z=x-c t. Bu çözüm formunun yerine kısmi diferansiyel denklemler bir sistem verir adi diferansiyel denklemler gezici dalga denklemleri olarak bilinir. Periyodik hareket eden dalgalar karşılık gelir limit döngüleri bu denklemlerin temelini oluşturur ve bu sayısal hesaplamalar. Standart hesaplama yaklaşımı sayısal devam seyahat eden dalga denklemlerinin. İlk önce bir devam ettirir kararlı hal bulmak için Hopf çatallanma nokta. Bu, periyodik seyahat eden dalga çözümlerinin bir dalı (ailesi) için başlangıç ​​noktasıdır. sayısal devam. Bazı (olağandışı) durumlarda, periyodik hareket eden dalga çözümlerinin bir dalının (ailesinin) her iki uç noktası da homoklinik çözümler[37] bu durumda kişi, sayısal çözüm gibi harici bir başlangıç ​​noktası kullanmak zorundadır. kısmi diferansiyel denklemler.

Periyodik seyahat dalgası istikrar hesaplanarak sayısal olarak da hesaplanabilir. spektrum. Bu, kısmi diferansiyel denklemlerin periyodik hareket eden dalga çözümlerinin spektrumunun tamamen aşağıdakilerden oluşması gerçeğiyle kolaylaştırılmıştır. temel spektrum.[38] Olası sayısal yaklaşımlar arasında Hill's yöntemi bulunur[39] ve spektrumun sayısal devamı.[15] İkinci yaklaşımın bir avantajı, sınırları hesaplamak için genişletilebilmesidir. parametre kararlı ve kararsız dalgalar arasındaki boşluk[40]

Yazılım: Ücretsiz açık kaynaklı yazılım Wavetrain paketi http://www.ma.hw.ac.uk/wavetrain periyodik hareket eden dalgaların sayısal çalışması için tasarlanmıştır.[41] Kullanma sayısal devam Wavetrain, kısmi diferansiyel denklemlerin periyodik hareket eden dalga çözümlerinin biçimini ve kararlılığını ve dalgaların bulunduğu ve kararlı oldukları parametre uzayının bölgelerini hesaplayabilir.

Başvurular

Bulunan periyodik hareket eden dalgalara benzeyen fenomen örnekleri deneysel olarak aşağıdakileri dahil edin.

  • Birçok doğal popülasyon, çok yıllık bolluk döngülerinden geçer. Bazı durumlarda bu popülasyon döngüleri mekansal olarak periyodik bir seyahat dalgası şeklinde düzenlenir. Bu davranış bulundu tarla fareleri Fennoscandia'da[13] ve Kuzey İngiltere,[14] geometrid güveler Kuzey Fennoscandia'da,[42] Avrupa Alpleri'ndeki karaçam budutları[21] ve kırmızı orman tavuğu İskocya'da.[43]
  • İçinde yarı çöller, bitki örtüsü genellikle kendi kendine organize olur mekansal desenler.[44] Yamaçlarda, bu tipik olarak, şeye paralel uzanan bitki örtüsü şeritlerinden oluşur. kontür çıplak zemin şeritleriyle ayrılmış; bu tür şeritli bitki örtüsü bazen şu şekilde bilinir: Kaplan çalı. Pek çok gözlemsel çalışma, şeritlerin yokuş yukarı yönde yavaş hareket ettiğini bildirmiştir.[45] Bununla birlikte, diğer bazı durumlarda veriler açıkça durağan modellere işaret eder,[46] ve hareket sorunu tartışmalı olmaya devam ediyor. Mevcut verilerle en tutarlı sonuç, bazı şeritli bitki örtüsü modellerinin hareket ederken diğerlerinin hareket etmediğidir.[47] Önceki kategorideki desenler, periyodik hareket eden dalgalar biçimindedir.
  • Gezici bantlar oluşur salınımlı ve heyecanlı kimyasal reaksiyonlar. 1970'lerde, Belousov-Zhabotinsky reaksiyonu[48] ve o dönemde periyodik hareket eden dalgalar üzerinde yapılan matematiksel çalışmalar için önemli bir motivasyon oluşturdular. Daha yeni araştırmalar, deneysel olarak gözlemlenen bantları ayrıntılı modelleme yoluyla periyodik hareket eden dalgaların matematiksel teorisiyle ilişkilendirme kapasitesinden de yararlandı.[49]
  • Güneşte periyodik hareket eden dalgalar meydana gelir. güneş döngüsü.[50][51] Güneş'in neslinin bir sonucudur. manyetik alan tarafından güneş dinamosu. Bu nedenle, bunlar güneş lekeleri.
  • İçinde hidrodinamik, konveksiyon desenler genellikle periyodik hareket eden dalgaları içerir. Belirli örnekler arasında ikili sıvı konveksiyonu bulunur[52] ve ısıtılmış tel konveksiyonu.[53]
  • Periyodik hareket eden dalga formu kalıpları, iki dönen merkezrik silindir arasındaki ince boşluğun yağla doldurulduğu "yazıcının dengesizliğinde" meydana gelir.[54]

Ayrıca bakınız

Referanslar

  1. ^ a b c d e f N. Kopell, L.N. Howard (1973) "Tepkime-difüzyon denklemlerine düzlem dalga çözümleri", Damızlık. Appl. Matematik. 52: 291–328.
  2. ^ a b c d I. S. Aranson, L. Kramer (2002) "Ginzburg-Landau karmaşık denkleminin dünyası", Rev. Mod. Phys. 74: 99–143. DOI: 10.1103 / RevModPhys.74.99
  3. ^ S. Coombes (2001) "Dendritik dalgaların sivri-dağınık-sivri uçlu modelinde periyodik hareket eden dalgalardan hareketli cephelere", Matematik. Biosci. 170: 155–172.DOI: 10.1016 / S0025-5564 (00) 00070-5
  4. ^ J.A. Sherratt, G. J. Lord (2007) "Yarı kurak ortamlarda bitki örtüsü şeritleri için bir modelde doğrusal olmayan dinamikler ve desen çatallanmaları", Theor. Popul. Biol. 71 (2007): 1–11.DOI: 10.1016 / j.tpb.2006.07.009
  5. ^ S. A. Gourley, N. F. Britton (1993) "Yerel olmayan etkileri olan bir popülasyon modelinin hareketli dalga çözümlerinin kararsızlığı", IMA J. Appl. Matematik. 51: 299–310.DOI: 10.1093 / imamat / 51.3.299
  6. ^ P. Ashwin, M. V. Bartuccelli, T. J. Bridges, S. A. Gourley (2002) "Uzamsal-zamansal gecikmeli KPP denklemi için seyahat cepheleri", Z. Angew. Matematik. Phys. 53: 103–122.DOI: 0010-2571 / 02 / 010103-20
  7. ^ M. Kot (1992) "Kesikli zamanda yolculuk dalgaları: ekolojik örnekler", J. Math. Biol. 30: 413-436. DOI: 10.1007 / BF00173295
  8. ^ M. D. S. Herrera, J. S. Martin (2009) "Senkronize durumların ve hareket eden dalgaların birleştirilmiş harita kafeslerinde ve bunların periyot ikiye katlayan kademelerinde analitik bir çalışma", Kaos, Solitonlar ve Fraktallar 42: 901–910.DOI: 10.1016 / j.chaos.2009.02.040
  9. ^ J. A. Sherratt (1996) "Bir deterministik hücresel otomata ailesinde periyodik hareket eden dalgalar", Physica D 95: 319–335.DOI: 10.1016 / 0167-2789 (96) 00070-X
  10. ^ M. Courbage (1997) "1 Boyutlu sonsuz hücresel otomatada hareket eden dalgaların bolluğu üzerine", Physica D 103: 133–144.DOI: 10.1016 / S0167-2789 (96) 00256-4
  11. ^ a b c J. A. Sherratt (1994) "Reaksiyon difüzyon dalgalarında düzensiz uyanmalar", Physica D 70: 370–382. DOI: 10.1016 / 0167-2789 (94) 90072-8
  12. ^ a b S.V. Petrovskii, H. Malchow (1999) "Bir av-yırtıcı sistemde minimal bir desen oluşumu modeli", Matematik. Comp. Modelleme 29: 49–63. DOI: 10.1016 / S0895-7177 (99) 00070-9
  13. ^ a b E. Ranta, V. Kaitala (1997) "Tarla faresi popülasyon dinamiklerinde seyahat eden dalgalar", Doğa 390: 456. DOI: 10.1038 / 37261
  14. ^ a b X. Lambin, D. A. Elston, S. J. Petty, J. L. MacKinnon (1998) "Tarla farelerinin döngüsel popülasyonlarında uzaysal asenkron ve periyodik hareket eden dalgalar", Proc. R. Soc. Lond. B 265: 1491–1496. DOI: 10.1098 / rspb.1998.0462
  15. ^ a b c d J.D.M. Rademacher, B. Sandstede, A. Scheel (2007) "Devam kullanarak mutlak ve temel spektrumların hesaplanması", Physica D 229: 166–183. DOI: 10.1016 / j.physd.2007.03.016
  16. ^ a b c M. J. Smith, J. D. M. Rademacher, J. A. Sherratt (2009) "Dalgaların mutlak kararlılığı lambda-omega tipi reaksiyon-difüzyon sistemlerindeki uzay-zamansal dinamikleri açıklayabilir", SIAM J. Appl. Dyn. Sistemler 8: 1136–1159. DOI: 10.1137 / 090747865
  17. ^ K. Maginu (1981) "Reaksiyon difüzyon sistemlerinde büyük uzaysal periyotlu periyodik hareket eden dalga çözümlerinin kararlılığı" J. Diff. Eqns. 39: 73–99.10.1016 / 0022-0396 (81) 90084-X
  18. ^ M. J. Smith, J.A. Sherratt (2007) "Eşit olmayan difüzyon katsayılarının salınımlı reaksiyon-difüzyon sistemlerinde periyodik hareket eden dalgalar üzerindeki etkileri", Physica D 236: 90–103. DOI: 10.1016 / j.physd.2007.07.013
  19. ^ B. Sandstede, A. Scheel (2000) "Sınırsız ve geniş sınırlı alanlarda dalgaların mutlak ve konvektif kararsızlıkları", Physica D 145: 233–277.DOI: 10.1016 / S0167-2789 (00) 00114-7
  20. ^ A. L. Kay, J. A. Sherratt (2000) "Uzaysal gürültü, sonlu bölgelerdeki salınımlı sistemlerde periyodik dalga modelini stabilize eder", SIAM J. Appl. Matematik. 61: 1013–1041.DOI: 10.1137 / S0036139999360696
  21. ^ a b D. M. Johnson, O. N. Bjornstad, A.M. Liebhold (2006) "Manzara mozaiği gezici böcek salgınlarına neden oluyor", Oekoloji 148: 51–60.DOI: 10.1007 / s00442-005-0349-0
  22. ^ a b K. Nozaki, N. Bekki (1983) "Ginzburg-Landau denkleminde örüntü seçimi ve kaosa uzay-zamansal geçiş", Phys. Rev. Lett. 51: 2171-2174. DOI: 10.1103 / PhysRevLett.51.2171
  23. ^ A. Tsameret, V. Steinberg (1994) "Eksenel akışlı bir Couette-Taylor sisteminde rekabet halleri", Phys. Rev. E 49: 4077-4086. DOI: 10.1103 / PhysRevE.49.4077
  24. ^ M. Ipsen, L. Kramer, P.G. Sorensen (2000) "Kimyasal reaksiyon-difüzyon sistemlerinin tanımı için genlik denklemleri", Phys. Rep. 337: 193–235.DOI: 10.1016 / S0370-1573 (00) 00062-4
  25. ^ GİBİ. Mihailov, K. Showalter (2006) "Kimyasal sistemlerde dalgaların, örüntülerin ve türbülansın kontrolü", Phys. Rep. 425: 79–194. DOI: 10.1016 / j.physrep.2005.11.003
  26. ^ J.A. Sherratt, M. A. Lewis, A. C. Fowler (1995) "İstilanın ardından ekolojik kaos", Proc. Natl. Acad. Sci. Amerika Birleşik Devletleri 92: 2524–2528.10.1073 / pnas.92.7.2524
  27. ^ a b S.V. Petrovskii, H. Malchow (2001) "Kaos dalgası: mekansal-zamansal nüfus dinamiklerinde yeni model oluşum mekanizması", Theor. Pop. Biol. 59: 157–174.DOI: 10.1006 / tpbi.2000.1509
  28. ^ J. A. Sherratt, X. Lambin, C. J. Thomas, T.N. Sherratt (2002) "Döngüsel avcı-av sistemlerinde peyzaj özellikleriyle periyodik dalgaların oluşturulması" Proc. R. Soc. Lond. B 269: 327–334.DOI: 10.1098 / rspb.2001.1890
  29. ^ M. Sieber, H. Malchow, S.V. Petrovskii (2010) "Salınımlı reaksiyon-difüzyon sistemlerinde periyodik hareket eden dalgaların gürültü kaynaklı bastırılması", Proc. R. Soc. Lond. A 466: 1903–1917.DOI: 10.1098 / rspa.2009.0611
  30. ^ J.A. Sherratt (2008) "Salınımlı reaksiyon-difüzyon denklemlerinde Robin ve Dirichlet sınır koşulları tarafından periyodik hareket eden dalga oluşumunun bir karşılaştırması". IMA J. Appl. Matematik. 73: 759-781.DOI: 10.1093 / imamat / hxn015
  31. ^ V. N. Biktashev, M. A. Tsyganov (2009) "Çapraz difüzyonlu salınımlı sistemlerde spontane hareket eden dalgalar", Phys. Rev. E 80: sanat. Hayır. 056111.DOI: 10.1103 / PhysRevE.80.056111
  32. ^ M. R. Garvie, M. Golinski (2010) "Uzamsal olarak genişletilmiş avcı-av etkileşimleri için metapopülasyon dinamikleri", Ekolojik Karmaşıklık 7: 55–59.DOI: 10.1016 / j.ecocom.2009.05.001
  33. ^ J. A. Sherratt (1994) "λ-ω tipi reaksiyon-difüzyon denklemlerinde periyodik düzlem dalgalarının evrimi üzerine", SIAM J. Appl. Matematik. 54: 1374–1385. DOI: 10.1137 / S0036139993243746
  34. ^ a b N. Bekki, K. Nozaki (1985) "Genelleştirilmiş Ginzburg-Landau denkleminde uzamsal desen ve deliklerin oluşumları", Phys. Lett. Bir 110: 133–135.DOI: 10.1016 / 0375-9601 (85) 90759-5
  35. ^ J. A. Sherratt (2003) "Salınımlı reaksiyon-difüzyon sistemlerinde Dirichlet sınır koşulları ile periyodik hareket eden dalga seçimi", SIAM J. Appl. Matematik. 63: 1520–1538. DOI: 10.1137 / S0036139902392483
  36. ^ J. Lega (2001) "Ginzburg-Landau karmaşık denkleminin gezici delik çözümleri: bir inceleme", Physica D 152: 269–287. DOI: 10.1016 / S0167-2789 (01) 00174-9
  37. ^ E. J. Doedel, J. P. Kernevez (1986) "AUTO: adi diferansiyel denklemlerde devam ve çatallanma problemleri için yazılım", Uygulamalı Matematik Raporu, California Teknoloji Enstitüsü, Pasadena, ABD
  38. ^ Bölüm 3.4.2, B. Sandstede (2002) "Gezici dalgaların kararlılığı". İçinde: B. Fiedler (ed.) Dinamik Sistemler El Kitabı II, North-Holland, Amsterdam, s. 983–1055. http://www.dam.brown.edu/people/sandsted/publications/survey-stability-of-waves.pdf Arşivlendi 2013-09-27 de Wayback Makinesi
  39. ^ B. Deconinck, J. N. Kutz (2006) "Floquet – Fourier – Hill yöntemini kullanarak doğrusal operatörlerin spektrumlarını hesaplama", J. Comput. Phys. 219: 296–321. DOI: 10.1016 / j.jcp.2006.03.020
  40. ^ J. A. Sherratt (2013) "Kısmi diferansiyel denklemlerin kararlı ve kararsız periyodik hareket eden dalga (dalgalanma) çözümleri arasındaki parametre uzayındaki sınırların sayısal devamı", Adv. Bilgisayar. Matematik, Basında. DOI: 10.1007 / s10444-012-9273-0
  41. ^ J.A. Sherratt (2012) "Kısmi diferansiyel denklemlerin periyodik hareket eden dalga (dalga düzeni) çözümlerini incelemek için sayısal devam yöntemleri",Appl. Matematik. Hesaplama 218: 4684–4694. DOI: 10.1016 / j.amc.2011.11.005
  42. ^ A. C. Nilssen, O. Tenow, H. Bylund (2007) "Dalgalar ve eşzamanlılık Epirrita autumnata / Operophtera brumata salgınlar II. Sunspot aktivitesi döngüsel salgınları açıklayamaz ", J. Animal Ecol. 76: 269–275.DOI: 10.1111 / j.1365-2656.2006.01205.x / tam
  43. ^ R. Moss, D.A. Elston, A. Watson (2000) "Kırmızı orman tavuğu popülasyon döngüleri sırasında uzaysal eşzamansız ve demografik gezici dalgalar", Ekoloji 81: 981-989. DOI: 10.1890 / 0012-9658
  44. ^ M. Rietkerk, S.C. Dekker, P.C. de Ruiter, J. van de Koppel (2004) "Ekosistemlerde kendi kendine organize düzensizlik ve yıkıcı değişimler", Bilim 305: 1926–1929.DOI: 10.1126 / science.1101867
  45. ^ C. Valentin, J. M. d'Herbes, J. Poesen (1999) "Şeritli bitki örtüsü desenlerinin toprak ve su bileşenleri", Catena 37: 1-24. DOI: 10.1016 / S0341-8162 (99) 00053-3
  46. ^ D. L. Dunkerley, K. J. Brown (2002) "Avustralya'nın kurak bölgesinde eğik bitki örtüsü şeritlenmesi: örüntü evrimi ve bakım teorileri için çıkarımlar", J. Arid Environ. 52: 163–181. DOI: 10.1006 / jare.2001.0940
  47. ^ V. Deblauwe (2010) "Ortamda bitki örtüsü oto-organizmalarının yapılarının modülasyonu / Kurak iklimlerde kendi kendine organize bitki örtüsü modeli modülasyonu". Doktora tezi, Universite Libre de Bruxelles."Arşivlenmiş kopya". Arşivlenen orijinal 2013-09-27 tarihinde. Alındı 2013-01-09.CS1 Maint: başlık olarak arşivlenmiş kopya (bağlantı)
  48. ^ N. Kopell, L.N. Howard (1973) "Belousov reaksiyonunda yatay bantlar", Bilim 180: 1171–1173. DOI: 10.1126 / science.180.4091.1171
  49. ^ G. Bordyugov, N. Fischer, H. Engel, N. Manz, O. Steinbock (2010) "Belousov-Zhabotinsky reaksiyonunda anormal dağılım: deneyler ve modelleme", Physica D 239: 766–775. DOI: 10.1016 / j.physd.2009.10.022
  50. ^ M.R.E.Proctor (2006) "Dinamo eylemi ve güneş". İçinde: M. Rieutord, B. Dubrulle (editörler) Yıldız Akışkan Dinamiği ve Sayısal Simülasyonlar: Güneşten Nötron Yıldızlarına, EAS Yayınları Serisi 21: 241–273. http://www.damtp.cam.ac.uk/user/mrep/solcyc/paper.pdf
  51. ^ M.R.E. Proctor, E. A. Spiegel (1991) "Waves of solar activity". İçinde: Güneş ve Soğuk Yıldızlar: Aktivite, Manyetizma, Dinamolar (Fizikte Ders Notları 380) sayfa 117–128.DOI: 10.1007 / 3-540-53955-7_116
  52. ^ E. Kaplan, V. Steinberg (1993) "Faz kayması, adiyabatik olmayan etki ve yürüyen dalgaların bir kaynağının dinamikleri", Phys. Rev. Lett. 71: 3291–3294. DOI: 10.1103 / PhysRevLett.71.3291
  53. ^ L. Pastur, M. T. Westra, D. Snouck, W. van de Water, M. van Hecke, C. Storm, W. van Saarloos (2003) "Tek boyutlu gezici dalga konveksiyon deneyinde kaynaklar ve delikler", Phys. Rev. E 67: sanat. Hayır. 036305. DOI: 10.1103 / PhysRevE.67.036305
  54. ^ P. Habdas, M. J. Case, J. R. de Bruyn (2001) "Tek boyutlu hareket eden parmak modelinde lavabo ve kaynak kusurlarının davranışı", Phys. Rev. E 63: sanat hayır. 066305.DOI: 10.1103 / PhysRevE.63.066305