Eşit kürelerin yakın paketlenmesi - Close-packing of equal spheres - Wikipedia

İçinde geometri, eşit yakın paketleme küreler sonsuz, düzenli bir düzenlemede (veya) uyumlu kürelerin yoğun bir düzenlemesidir kafes ). Carl Friedrich Gauss en yüksek ortalama yoğunluğun - yani, kürelerin kapladığı en büyük alan fraksiyonunun - kafes paketleme
Aynısı paketleme yoğunluğu aynı zamanda, istifleme yönünde periyodik olmayan yapılar dahil olmak üzere, aynı yakın paketlenmiş küre düzlemlerinin alternatif istiflenmesiyle de elde edilebilir. Kepler varsayımı bunun, ister düzenli ister düzensiz olsun, herhangi bir küre düzenlemesiyle elde edilebilecek en yüksek yoğunluk olduğunu belirtir. Bu varsayım tarafından kanıtlandı T. C. Hales.[1][2] En yüksek yoğunluk yalnızca 1, 2, 3, 8 ve 24 boyutlarında bilinir.[3]
Birçok kristal yapılar, tek bir tür atomun yakın paketlenmesine veya aralarındaki boşlukları dolduran daha küçük iyonlarla büyük iyonların yakın paketlenmesine dayanır. Enerji açısından kübik ve altıgen dizilimler birbirine çok yakındır ve hangi formun ilk ilkelerden tercih edileceğini kestirmek zor olabilir.
FCC ve HCP Kafesleri

| fcc | hcp | |
|---|---|---|
 |  |  |
| fcc düzenleme kare veya üçgen olmak üzere iki farklı düzlemde yönlendirilebilir. Bunlar şurada görülebilir: küpoktahedron bir merkezi küre etrafında 12 komşu kürenin konumlarını temsil eden 12 köşeli. hcp düzenleme üçgen yönde görülebilir, ancak iki kürenin konumunu bir üçgen orthobicupola aranjman. | ||
Bu en yüksek ortalama yoğunluğa ulaşan iki basit düzenli kafes vardır. Arandılar yüz merkezli kübik (fcc) (olarak da adlandırılır kübik yakın paketlenmiş) ve altıgen yakın paketlenmiş (hcp), onlara göre simetri. Her ikisi de üçgen bir döşemenin köşelerinde düzenlenmiş küre tabakalarına dayanmaktadır; yaprakların birbiri üzerine nasıl istiflendiği konusunda farklılık gösterirler. Fcc kafesi, matematikçiler tarafından A tarafından üretilen kafes olarak da bilinir.3 kök sistem.[4]
Cannonball sorunu

Kürelerin yakın paketlenmesi sorunu ilk olarak matematiksel olarak analiz edildi. Thomas Harriot 1587 civarı, gemilere gülle yığılmasına ilişkin bir sorudan sonra ona Sir tarafından Walter Raleigh Amerika gezilerinde.[5] Top topları genellikle dikdörtgen veya üçgen bir ahşap çerçeve içinde istiflenir ve üç taraflı veya dört taraflı bir piramit oluşturur. Her iki düzenleme de zemine göre farklı yönelimle yüz merkezli bir kübik kafes oluşturur. Altıgen yakın paketleme, altıgen tabanlı altı kenarlı bir piramit ile sonuçlanır.

gülle sorunu hangi top güllelerinin düz kare düzenlemelerinin bir kare piramide istiflenebileceğini sorar. Édouard Lucas problemi şu şekilde formüle etti: Diofant denklemi veya ve tek çözümün ve . Buraya piramidal istifleme düzenlemesindeki katman sayısıdır ve düz kare düzenlemede bir kenar boyunca uzanan güllelerin sayısıdır.
Konumlandırma ve aralık
Hem fcc hem de hcp düzenlemelerinde her kürenin on iki komşusu vardır. Her küre için altı küre ile çevrili bir boşluk vardır (sekiz yüzlü ) ve dört küre (tetrahedral) ile çevrili iki küçük boşluk. Bu boşlukların merkezlerini çevreleyen kürelerin merkezlerine olan mesafeleri √3⁄2 tetrahedral için ve √2 oktahedral için, küre yarıçapı 1 olduğunda.
Konumlandırma A'ya sahip bir referans katmanına göre, iki konumlandırma daha B ve C mümkündür. Aynı dizinin hemen tekrarı olmaksızın her A, B ve C dizisi mümkündür ve belirli bir yarıçaptaki küreler için eşit derecede yoğun bir paketleme sağlar.
En düzenli olanlar
- fcc = ABC ABC ABC ... (her üçüncü katman aynıdır)
- hcp = AB AB AB AB ... (diğer her katman aynıdır).
Kristalograftan sonra bazen topluca "Barlow paketleri" olarak anılan sayılamayacak kadar düzensiz sonsuz sayıda düzensiz düzlem düzenlemeleri (örneğin ABCACBABABAC ...) vardır. William Barlow[6]
Yakın paketlemede, merkezdeki kürelerin merkezden merkeze aralığı xy düzlem, bir küre çapındaki bir eğim (küre merkezleri arasındaki mesafe) ile basit bir bal peteği benzeri mozaiktir. Küre merkezleri arasındaki mesafe, z (dikey) eksen:
nerede d bir kürenin çapıdır; bu, sıkışık kürelerin dörtyüzlü düzenlemesinden kaynaklanır.
koordinasyon numarası hcp ve fcc'nin oranı 12'dir ve atomik paketleme faktörleri (APF'ler) yukarıda belirtilen sayıya eşittir, 0.74.
| Hcp ve fcc arasında karşılaştırma |
|---|
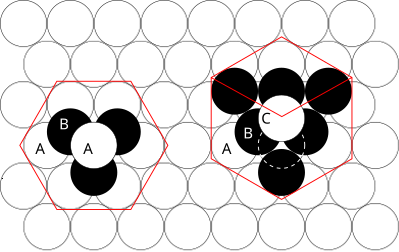 |
| Şekil 1 - hcp kafes (solda) ve fcc kafes (sağda). Her bir ilgili ana hat Bravais kafes kırmızı ile gösterilmiştir. Harfler hangi katmanların aynı olduğunu gösterir. Hcp matrisinde tüm kürelerin aynı konumda olduğu iki "A" katmanı vardır. Fcc yığınındaki üç katman da farklıdır. Fcc yığınlamasının, kesik çizgilerle gösterildiği gibi en üstteki kürenin çevrilmesiyle hcp yığınlamasına dönüştürülebileceğini unutmayın. |
 |  |
| şekil 2 - Burada gösterilen on bir küreden oluşan bir yığın hcp gösterilen kafes Şekil 1. Hcp yığını, gösterilen fcc yığınının ilk 3 katmanından farklıdır. Figür 3 yalnızca en düşük kademede; uygun bir döndürme veya çevirme ile fcc'ye değiştirilebilir. | Figür 3 – Thomas Harriot, 1585 dolaylarında, ilk önce gülle düzenlemesi veya gülle yığını, olan fcc kafes. Normalin her kenarı boyunca bitişik topların dörtyüzlü yığını çevreleyenlerin tümü birbiriyle doğrudan temas halindedir. Bu, gösterildiği gibi bir hcp kafesinde meydana gelmez. şekil 2. |
Kafes üretimi
Herhangi bir küre paketleme kafesi oluştururken, dikkat edilmesi gereken ilk gerçek, iki küre temas ettiğinde, bir kürenin merkezinden diğerinin merkezine temas noktasını kesen düz bir çizgi çizilebileceğidir. En kısa yol boyunca merkezler arasındaki mesafe, yani düz çizgi bu nedenle r1 + r2 nerede r1 ilk kürenin yarıçapı ve r2 saniyenin yarıçapıdır. Yakın paketlemede tüm küreler ortak bir yarıçapı paylaşır, r. Bu nedenle, iki merkezin uzaklığı 2 olacaktır.r.
Basit hcp kafes

Bir A-B-A-B -... altıgen kapalı küreler oluşturmak için, kafesin koordinat noktaları kürelerin merkezleri olacaktır. Diyelim ki amaç hcp'ye göre bir kutuyu kürelerle doldurmaktır. Kutu, x-y-z koordinat alanı.
Önce bir sıra küre oluşturun. Merkezlerin hepsi düz bir çizgi üzerinde olacak. Onların x- koordinat 2'ye göre değişirr kürelerin her bir merkezi arasındaki mesafe 2 olduğu içinr. y-koordinat ve z-koordinatı aynı olacaktır. Basit olması için, topların ilk sıra olduğunu ve onların y- ve zkoordinatlar basittir r, böylece yüzeyleri sıfır düzlemlere dayanır. İlk sıranın merkezlerinin koordinatları şöyle görünecektir (2r, r, r), (4r, r, r), (6r ,r, r), (8r ,r, r), ... .
Şimdi, bir sonraki küre sırasını oluşturun. Yine, merkezlerin hepsi düz bir çizgi üzerinde uzanacak x-iki koordinat farklılıklarırama bir mesafe kayması olacak r içinde x-yönde, böylece bu satırdaki her kürenin merkezi, x-İki kürenin ilk satırda temas ettiği yerin koordinatı. Bu, yeni satırdaki tüm küreler ilk satırın iki küresine dokunana kadar yeni satırın kürelerinin ilk satıra daha yakın kaymasını sağlar. Yeni kürelerden beri dokunma iki küre, merkezleri bu iki komşunun merkezleriyle eşkenar üçgen oluşturur. Yan uzunlukların hepsi 2ryani yükseklik veya y- Satırlar arasındaki koordinat farkı √3r. Böylece, bu satır aşağıdaki gibi koordinatlara sahip olacaktır:
Bu satırın ilk küresi, orijinal satırdaki yalnızca bir küreye dokunur, ancak konumu satırın geri kalanıyla uyumludur.
Bir sonraki satır, bu x-e göre koordine et r ve y-e göre koordine et √3. Ulaşana kadar satır ekleyin x ve y kutunun maksimum sınırları.
Bir A-B-A-B -... istifleme modelinde, tek numaralı yüzeyleri Kürelerin sayısı, aralık farkı dışında tamamen aynı koordinatlara sahip olacaktır. zkoordinatlar ve çift numaralı yüzeyleri kürelerin yüzdesi aynı şeyi paylaşacak x- ve y- koordinatlar. Her iki tür düzlem de yukarıda belirtilen model kullanılarak oluşturulur, ancak başlangıç noktası ilk satırın ilk küresi farklı olacaktır.
Yukarıda tam olarak 1. düzlemi, A düzlemi olarak tanımlanan düzlemi kullanarak, bu düzlemin üstüne, A-düzlemindeki üç küre ile temas edecek şekilde bir küre yerleştirin. Üç kürenin hepsi zaten birbirine dokunarak bir eşkenar üçgen oluşturuyor ve hepsi yeni küreyle temas ettiğinden, dört merkez bir normal dörtyüzlü.[7] Tüm taraflar 2'ye eşitr çünkü tüm kenarlar birbirine değen iki küre ile oluşturulmuştur. Hangisinin yüksekliği veya z-iki "uçak" arasındaki koordinat farkı √6r2/3. Bu, içindeki ofsetlerle birlikte x ve yKoordinatlar, B düzlemindeki ilk sıranın merkezlerini verir:
İkinci sıranın koordinatları, yukarıda açıklanan ilk düzeni izler ve şunlardır:
Bir sonraki düzlem olan A düzlemiyle olan fark yine √6r2/3 içinde zyön ve bir kayma x ve y bunlarla eşleşmek için x- ve y-İlk A düzleminin koordinatları.[8]
Genel olarak, küre merkezlerinin koordinatları şu şekilde yazılabilir:
nerede ben, j ve k 0'dan başlayan endekslerdir x-, y- ve z- koordinatlar.
Miller endeksleri

Vektörler ve atomik düzlem aileleri gibi hcp sistemlerinin kristalografik özellikleri, dört değer kullanılarak tanımlanabilir. Miller endeksi gösterim ( hkil ) üçüncü indeks ben uygun ancak dejenere bir bileşeni belirtir -h − k. h, ben ve k indeks yönleri 120 ° ile ayrılır ve bu nedenle ortogonal değildir; l bileşen karşılıklı olarak diktir. h, ben ve k dizin yönleri.
Kalan alanı doldurmak
Fcc ve hcp paketleri, en yüksek simetriye (en küçük tekrar birimleri) sahip eşit kürelerin bilinen en yoğun ambalajlarıdır. küre paketleri biliniyor ama içeriyorlar eşit olmayan küre paketleme Boşluğu tamamen dolduran 1'lik bir paketleme yoğunluğu, küresel olmayan şekiller gerektirir, örneğin petek.
İki küre arasındaki her temas noktasını, temas eden kürelerin merkezlerini birleştiren bir kenarla değiştirmek, eşit kenar uzunluklarına sahip tetrahedronlar ve oktahedronlar üretir. Fcc düzenlemesi, dörtyüzlü-oktahedral petek Hcp düzenlemesi, döner dörtyüzlü-oktahedral bal peteği Bunun yerine, her küre, uzayda kendisine başka herhangi bir küreden daha yakın olan noktalarla büyütülürse, bu peteklerin ikilileri üretilir: eşkenar dörtgen on iki yüzlü petek fcc için ve ikizkenar yamuk-eşkenar dörtgen petek hcp için.
Kabarcıklar arasındaki boşluklardaki su dışarı aktığında sabunlu suda fcc veya hcp düzenlemesinde küresel baloncuklar görünür. Bu model aynı zamanda eşkenar dörtgen on iki yüzlü petek veya ikizkenar yamuk-eşkenar dörtgen petek. Bununla birlikte, çok küçük sıvı içerikli bu tür fcc veya hcp köpükleri, tatmin etmedikleri için kararsızdır. Plato kanunları. Kelvin köpük ve Weaire – Phelan köpüğü çok küçük sıvı içeriği sınırında daha küçük arayüz enerjisine sahip olduğundan daha kararlıdır.[9]
Ayrıca bakınız
Notlar
- ^ Hales, T. C. (1998). "Kepler varsayımına genel bir bakış". arXiv:math / 9811071v2.
- ^ Szpiro, George (2003). "Matematik: İspat birikiyor mu?". Doğa. 424 (6944): 12–13. Bibcode:2003Natur.424 ... 12S. doi:10.1038 / 424012a.
- ^ Cohn, H .; Kumar, A .; Miller, S. D .; Radchenko, D .; Viazovska, M. (2017). "24 boyutunda küre paketleme sorunu". Matematik Yıllıkları. 185 (3): 1017–1033. arXiv:1603.06518. doi:10.4007 / yıllıklar.2017.185.3.8.
- ^ Conway, John Horton; Sloane, Neil James Alexander; Bannai, Eiichi (1999). Küre paketleri, kafesler ve gruplar. Springer. Bölüm 6.3.
- ^ Canım, David. "Cannonball Problemi". İnternet Bilim Ansiklopedisi.
- ^ Barlow, William (1883). "Kristallerin İç Simetrisinin Muhtemel Doğası" (PDF). Doğa. 29 (738): 186–188. Bibcode:1883Natur..29..186B. doi:10.1038 / 029186a0.
- ^ "Küre Ambalajda". Grunch.net. Alındı 2014-06-12.
- ^ Weisstein, Eric W. "Altıgen Kapalı Ambalaj". MathWorld.
- ^ Cantat Isabelle; Cohen-Addad, Sylvie; Elias, Floransa; Graner, François; Höhler, Reinhard; Flatman, Ruth; Pitois, Olivier (2013). Köpükler, Yapı ve Dinamikler. Oxford: Oxford University Press. ISBN 9780199662890.












![{ displaystyle { begin {bmatrix} 2i + ((j + k) { bmod {2}}) { sqrt {3}} sol [j + { frac {1} {3}} ( k { bmod {2}}) sağ] { frac {2 { sqrt {6}}} {3}} k end {bmatrix}} r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89bb83425e28ac94a674a3f1b10f04541208ef7a)