Daire paketleme - Circle packing

İçinde geometri, daire paketleme herhangi bir üst üste binme olmayacak ve böylece bir üst üste binme oluşturmadan hiçbir daire genişletilemeyecek şekilde belirli bir yüzey üzerindeki dairelerin (eşit veya değişen boyutlarda) düzenlenmesinin incelenmesidir. Ilişkili paketleme yoğunluğu, ηbir düzenlemenin, dairelerin kapladığı yüzeyin oranıdır. Daha yüksek boyutlara genellemeler yapılabilir - buna küre paketleme, genellikle yalnızca aynı alanlarla ilgilenir.
Daire, üzerinde 0.9069'luk nispeten düşük bir maksimum paketleme yoğunluğuna sahipken Öklid düzlemi, aralarında bile mümkün olan en düşük değere sahip değil merkezi simetrik dışbükey şekiller. Bir uçağa sığacak bu tür "en kötü" şekil belirlenmemiştir, ancak düzleştirilmiş sekizgen merkezi olarak simetrik dışbükey herhangi bir şeklin bilinen en düşük maksimum paketleme yoğunluğu olan yaklaşık 0.902414'lük bir paketleme yoğunluğuna sahiptir.[1](İçbükey şekillerin paketleme yoğunlukları, örneğin yıldız çokgenleri keyfi olarak küçük olabilir.)
Matematiğin genel olarak "daire paketleme" olarak bilinen dalı, rastgele boyutlandırılmış dairelerin paketlemelerinin geometrisi ve kombinatorikleriyle ilgilidir: bunlar, konformal haritalama, Riemann yüzeyleri ve benzerleri.
Uçakta salmastralar


İki boyutlu Öklid uzayında, Joseph Louis Lagrange 1773'te dairelerin en yüksek yoğunluklu kafes düzenlemesinin altıgen paketleme düzenlemesi,[2] dairelerin merkezlerinin bir altıgen kafes (bir gibi kademeli satırlar bal peteği ) ve her daire 6 başka daire ile çevrilidir. Çaplı daireler için bu düzenlemenin yoğunluğu D, dır-dir
D aynı zamanda ilk şekildeki altıgenin kenarıdır. İlk dönem Yukarıdaki oran, altıgenin çevrelediği tüm dairelerin ve kısmi dairelerin alanlarının toplamıdır. İkinci dönem altıgenin kendisinin alanıdır.
Eşit dairelerin altıgen paketinin bir kesri doldurduğu bulundu. alan - periyodik ambalajlar için maksimum olduğu kanıtlanmıştır. Carl Friedrich Gauss 1831'de.[3] Sonra, Axel Thue Bunun 1890'da optimal olduğuna dair ilk kanıtı sağladı ve altıgen kafesin hem normal hem de düzensiz tüm olası daire paketlerinin en yoğun olduğunu gösterdi. Ancak kanıtı bazıları tarafından eksik kabul edildi. İlk titiz kanıt atfedilir László Fejes Tóth 1940'ta.[2][4]
Diğer uçta, Böröczky, rijit bir şekilde paketlenmiş dairelerin keyfi olarak düşük yoğunluklu düzenlemelerinin var olduğunu gösterdi.[5][6]
Tek tip ambalajlar
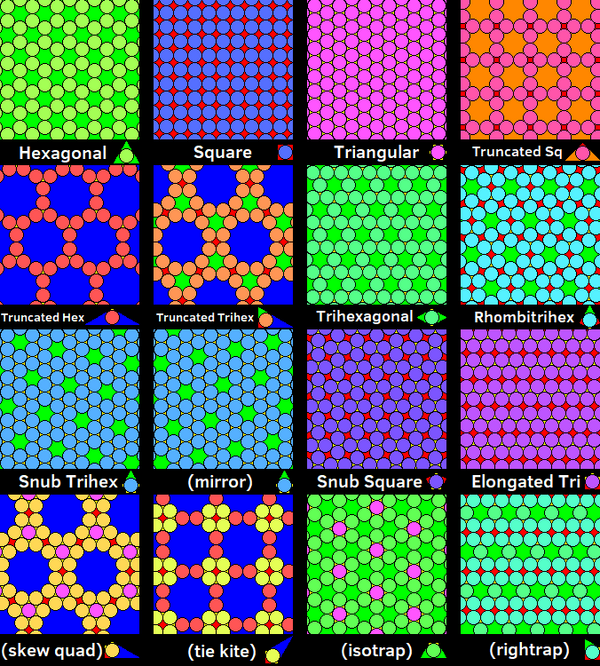
11'e göre 11 daire paketi vardır. tek tip döşemeler uçağın.[7] Bu paketlerde, her daire yansıma ve döndürme yoluyla diğer her daireye eşlenebilir. altıgen boşluklar bir daire ile doldurulabilir ve on ikigen boşluklar 7 daire ile doldurularak 3 üniform ambalajlar oluşturulabilir. kesik triheksagonal döşeme Her iki tip boşluk ile 4'lü salmastra olarak doldurulabilir. keskin altıgen döşeme iki ayna görüntüsü formuna sahiptir.
Küre üzerindeki ambalajlar
İlgili bir problem, belirli bir yüzey içinde uzanmakla sınırlandırılmış özdeş olarak etkileşen noktaların en düşük enerjili düzenlemesini belirlemektir. Thomson sorunu bir kürenin yüzeyindeki özdeş elektrik yüklerinin en düşük enerji dağılımıyla ilgilenir. Tammes sorunu bunun bir genellemesidir, küre üzerindeki daireler arasındaki minimum mesafeyi maksimize etmekle ilgilenir. Bu, bir küre üzerinde nokta olmayan yükleri dağıtmaya benzer.
Sınırlı alanlarda ambalajlar

Ambalaj çemberleri basit sınırlı şekillerde yaygın bir problem türü eğlence matematiği. Kap duvarlarının etkisi önemlidir ve altıgen istifleme genellikle az sayıda daire için uygun değildir.
Eşitsiz daireler
Dairelerin boyutlarının tek tip olmamasına izin veren bir dizi problem de vardır. Böyle bir uzantı, iki belirli daire boyutuna sahip bir sistemin mümkün olan maksimum yoğunluğunu bulmaktır (a ikili sistemi). Yalnızca dokuz belirli yarıçap oranı izin verir kompakt paketleme, temas halindeki her daire çiftinin diğer iki daire ile karşılıklı temas halinde olduğu zamandır (çizgi parçaları, temas eden daire merkezinden daire merkezine doğru çizildiğinde, yüzeyi üçgenleştirirler).[7] Tüm bu yarıçap oranları için, bu yarıçap oranına sahip disk karışımları için mümkün olan maksimum paketleme fraksiyonunu (muntazam boyutlu disklerin üzerinde) sağlayan kompakt bir paketleme bilinmektedir.[9] Dokuzunun tümü, tek tip altıgen salmastradan daha yoğun orana özgü salmastralara sahiptir ve kompakt salmastralar olmadan bazı yarıçap oranlarında olduğu gibi.[10]
Ayrıca, yarıçap oranının 0.742'nin üzerinde olması durumunda, ikili bir karışımın, tek tip boyutlu disklerden daha iyi toplanamayacağı da bilinmektedir.[8] Bu tür ikili ambalajlarda daha küçük oranlarda elde edilebilecek yoğunluk için üst sınırlar da elde edilmiştir.[11]
Başvurular
Çeyrek genlik modülasyonu daireleri bir faz genlik alanı. Bir modem verileri 2 boyutlu bir faz genliği düzleminde bir dizi nokta olarak iletir. Noktalar arasındaki boşluk, iletimin gürültü toleransını belirlerken, çevreleyen daire çapı gereken verici gücünü belirler. Performans en üst düzeye çıkarıldığında takımyıldız Kod noktalarının sayısı verimli bir çember paketlemenin merkezindedir. Pratikte, kod çözmeyi basitleştirmek için genellikle yetersiz dikdörtgen paketler kullanılır.
Çember paketleme temel bir araç haline geldi Japon kağıt katlama sanatı tasarım, çünkü bir origami figüründeki her eklenti bir kağıt çemberi gerektiriyor.[12] Robert J. Lang karmaşık origami figürlerinin tasarımına yardımcı olan bilgisayar programları geliştirmek için daire paketlemenin matematiğini kullandı.
Ayrıca bakınız
- Apollonian conta
- Bir kare içinde daire paketleme
- Daire içinde daire paketleme
- Ters mesafe
- Kepler varsayımı
- Malfatti çevreleri
- Paketleme sorunu
Referanslar
- ^ Weisstein, Eric W. "Düzleştirilmiş Sekizgen". MathWorld.
- ^ a b Chang, Hai-Chau; Wang, Lih-Chung (2010). "Dairesel Paketleme Üzerine Thue Teoreminin Basit Bir Kanıtı". arXiv:1009.4322 [math.MG ].
- ^ Wolfram Stephen (2002). Yeni Bir Bilim Türü. Wolfram Media, Inc. s.985. ISBN 1-57955-008-8.
- ^ Tóth, László Fejes (1940). "Über die dichteste Kugellagerung". Matematik. Z. 48: 676–684.
- ^ Böröczky, K. (1964). "Über stabil Kreis- und Kugelsysteme". Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, Sectio Mathematica. 7: 79–82.
- ^ Kahle, Matthew (2012). "Seyrek yerel olarak sıkışmış disk paketleri". Kombinatorik Yıllıkları. 16 (4): 773–780. doi:10.1007 / s00026-012-0159-0.
- ^ a b Tom Kennedy (2006). "İki boyutta disk ile uçağın kompakt paketleri". Ayrık ve Hesaplamalı Geometri. 35 (2): 255–267. arXiv:matematik / 0407145. doi:10.1007 / s00454-005-1172-4.
- ^ a b Heppes, Aladár (1 Ağustos 2003). "Uçakta En Yoğun İki Boyutlu Disk Salmastralarından Bazıları". Ayrık ve Hesaplamalı Geometri. 30 (2): 241–262. doi:10.1007 / s00454-003-0007-6.
- ^ Bédaride, Nicolas; Fernique, Thomas (17 Şubat 2020). "İkili Kompakt Disk Paketlerinin Yoğunluğu". arXiv:2002.07168. Alıntı dergisi gerektirir
| günlük =(Yardım) - ^ Kennedy, Tom (2004-07-21). "Daire Paketleri". Alındı 2018-10-11.
- ^ de Laat, David; de Oliveira Filho, Fernando Mario; Vallentin, Frank (12 Haziran 2012). "Birkaç yarıçaplı küreler için üst sınırlar". Matematik Forumu, Sigma. 2. arXiv:1206.2608. doi:10.1017 / fms.2014.24.
- ^ TED.com'un modern origami üzerine dersi "Robert Lang TED'de."
Kaynakça
- Wells D (1991). Meraklı ve İlginç Geometri Penguen Sözlüğü. New York: Penguin Books. pp.30–31, 167. ISBN 0-14-011813-6.
- Stephenson, Kenneth (Aralık 2003). "Çember Paketleme: Matematiksel Bir Hikaye" (PDF). American Mathematical Society'nin Bildirimleri. 50 (11).





