Denklemi tanımlama (fizik) - Defining equation (physics)

İçinde fizik, denklemleri tanımlama vardır denklemler yeni miktarları temel miktarlar açısından tanımlayan.^[1] Bu makale mevcut SI sistemi nın-nin birimleri, değil doğal veya karakteristik birimler.

Birimlerin ve fiziksel büyüklüklerin tanımı

Fiziksel büyüklükler ve birimler aynı hiyerarşiyi izler; seçilen temel miktarlar Sahip olmak tanımlı temel birimlerbunlardan diğerlerinden miktarlar türetilebilir ve karşılık gelen Türetilmiş birimler.

Renk karıştırma benzetmesi

Miktarların tanımlanması, renklerin karıştırılmasına benzer ve standart olmasa da benzer şekilde sınıflandırılabilir. Ana renkler, temel miktarlardır; ikincil (veya üçüncül vb.) olarak renkler türetilmiş miktarlardır. Renkleri karıştırmak, matematiksel işlemler kullanarak miktarları birleştirmeye benzer. Ama renkler olabilir ışık veya boya ve benzer şekilde birimler sistemi birçok formdan biri olabilir: SI gibi (şimdi en yaygın), CGS, Gauss, eski imparatorluk birimleri belirli bir formu doğal birimler veya hatta dikkate alınan fiziksel sisteme özgü keyfi olarak tanımlanmış birimler (karakteristik birimler ).

Temel bir miktar ve birim sisteminin seçimi keyfidir; ama bir kez seçti zorunlu tutarlılık için takip eden tüm analizler boyunca bağlı kalınmalıdır. Farklı birim sistemlerini karıştırmanın bir anlamı yoktur. Bir birimler sistemi seçmek, SI, CGS vb. Arasından bir sistem seçmek, boya veya açık renkler kullanmayı seçmek gibidir.

Bu benzetmenin ışığında, birincil tanımlar, tanımlayıcı bir denklemi olmayan, ancak tanımlanmış standart koşullara sahip temel miktarlardır, "ikincil" tanımlar, hem temel hem de "ikincil" miktarlar açısından miktarlar için "üçüncül", yalnızca temel miktarlar açısından tanımlanan miktarlardır. , baz, "ikincil" ve "üçüncül" nicelikler açısından nicelikler için "dörtlü", vb.

Motivasyon

Fiziğin çoğu, denklemlerin anlamlı olması için tanımların yapılmasını gerektirir.

Teorik çıkarımlar: Tanımlar, bir fizik dalının yeni anlayışlarına yol açabilecekleri için önemlidir. Klasik fizikte böyle iki örnek meydana geldi. Ne zaman entropi S tanımlandı - aralığı termodinamik ilişkilendirilerek büyük ölçüde genişletildi kaos ve düzensizlik enerji ve sıcaklık ile ilgili olabilecek sayısal bir miktar ile ikinci termodinamik yasa ve Istatistik mekaniği.^[2]

Ayrıca aksiyon işlevsel (ayrıca yazılmıştır S) (birlikte genelleştirilmiş koordinatlar ve Momenta ve Lagrange işlevi), başlangıçta alternatif bir formülasyon Klasik mekanik -e Newton yasaları, şimdi genel olarak modern fiziğin kapsamını genişletiyor - özellikle Kuantum mekaniği, parçacık fiziği, ve Genel görelilik.^[3]

Analitik uygunluk: Diğer denklemlerin daha kompakt bir şekilde yazılmasına izin verirler ve böylece daha kolay matematiksel manipülasyona izin verirler; Bir tanıma bir parametre dahil ederek, parametrenin oluşumları, ikame edilen miktara absorbe edilebilir ve denklemden çıkarılabilir.^[4]

Misal

Örnek olarak Ampère'nin dolaşım yasası (Maxwell düzeltmesi ile) keyfi bir akım taşıma için integral formda orkestra şefi içinde vakum (yani sıfır mıknatıslanma vadesi gelen orta, yani M = 0):^[5]

${ displaystyle oint _ {S} mathbf {B} cdot { rm {d}} mathbf {l} = mu _ {0} oint _ {S} sol ( mathbf {J} + epsilon _ {0} { frac { partial mathbf {E}} { kısmi t}} sağ) cdot { rm {d}} mathbf {A} , !}$

kurucu tanımı kullanarak

${ displaystyle mathbf {B} = mu _ {0} mathbf {H}, , !}$

ve mevcut yoğunluk tanımı

${ displaystyle I = oint _ {S} mathbf {J} cdot { rm {d}} mathbf {A}, , !}$

benzer şekilde yer değiştirme akımı yoğunluk

${ displaystyle mathbf {J} _ { rm {d}} = epsilon _ {0} { frac { kısmi mathbf {E}} { kısmi t}} , !}$ yer değiştirme akımına yol açan ${ displaystyle I_ {d} = oint _ {S} mathbf {J} _ { rm {d}} cdot { rm {d}} mathbf {A}, , !}$

sahibiz

${ displaystyle oint _ {S} mathbf {B} cdot { rm {d}} mathbf {l} = mu _ {0} oint _ {S} mathbf {J} cdot { rm {d}} mathbf {A} + mu _ {0} oint _ {S} mathbf {J} _ { rm {d}} cdot { rm {d}} mathbf {A} , , !}$

${ displaystyle oint _ {S} mathbf {H} cdot { rm {d}} mathbf {l} = I + I_ {d}, , !}$

Denklem aynı olsa bile yazmak daha kolaydır.

Karşılaştırma kolaylığı: Aksi halde belirsiz ve belirsiz görünebilecekleri zaman ölçümlerin karşılaştırılmasına izin verirler.

Misal

Temel bir örnek, kütle yoğunluğudur. Sadece kütleleri veya sadece hacimleri göz önüne alındığında, ne kadar maddenin çeşitli maddelerden oluştuğu net değildir. Her iki madde için de verildiğinde, kütle m birim hacim başına Vveya kütle yoğunluğu ρ maddeler arasında anlamlı bir karşılaştırma sağlar, çünkü her biri için sabit bir hacim, maddeye bağlı olarak bir kütle miktarına karşılık gelecektir. Bunu açıklamak için; iki A ve B maddesinin kütlesi varsa m_Bir ve m_B sırasıyla hacimleri işgal V_Bir ve V_B sırasıyla, kütle yoğunluğu tanımını kullanarak şunları verir:

ρ_Bir = m_Bir / V_Bir , ρ_B = m_B / V_B

bunu takiben şu görülebilir:

• Eğer m_Bir > m_B veya m_Bir < m_B ve V_Bir = V_B, sonra ρ_Bir > ρ_B veya ρ_Bir < ρ_B,
• Eğer m_Bir = m_B ve V_Bir > V_B veya V_Bir < V_B, sonra ρ_Bir < ρ_B veya ρ_Bir > ρ_B,
• Eğer ρ_Bir = ρ_B, sonra m_Bir / V_Bir = m_B / V_B yani m_Bir / m_B = V_Bir / V_B, eğer m_Bir > m_B veya m_Bir < m_B, sonra V_Bir > V_B veya V_Bir < V_B.

Matematiği mantıklı bir şekilde bu şekilde kullanmadan bu tür karşılaştırmaları yapmak sistematik olmayacaktır.

Tanımlama denklemlerinin oluşturulması

Tanımların kapsamı

Denklemleri tanımlamak normalde şu şekilde formüle edilir: temel cebir ve hesap, vektör cebir ve hesap veya en genel uygulamalar için tensör cebiri ve hesabı, çalışma ve sunum düzeyine, konunun karmaşıklığına ve uygulanabilirlik kapsamına bağlı olarak. Fonksiyonlar bir tanıma dahil edilebilir, çünkü hesap için bu gereklidir. Miktarlar da olabilir karmaşık - teorik avantaj için değerlidir, ancak fiziksel bir ölçüm için gerçek kısım ilgilidir, hayali kısım atılabilir. Daha ileri işlemler için, denklemin eşdeğer ancak alternatif bir biçimde, tanımın yararlı olması için diğer tanımlayıcı denklemler kullanılarak yazılması gerekebilir. Genellikle tanımlar temel cebirden başlayabilir, daha sonra vektörlere dönüşebilir, daha sonra sınırlayıcı durumlarda hesap kullanılabilir. Kullanılan çeşitli matematik seviyeleri tipik olarak bu kalıbı takip eder.

Tipik olarak tanımlar açıktır, yani tanımlayıcı nicelik denklemin konusudur, ancak bazen denklem açıkça yazılmaz - ancak tanımlayıcı miktar denklemi açık hale getirmek için çözülebilir. Vektör denklemleri için, bazen tanımlayıcı miktar bir çapraz veya nokta çarpımdadır ve bir vektör olarak açıkça çözülemez, ancak bileşenler çözebilir.

Akı F aracılığıyla yüzey, dS ... diferansiyel vektör alanı eleman n ... normal birim yüzeye. Buradaki fiziksel örnekler için, akım yoğunluğu J veya manyetik alan B olabilir F diyagramda.

Açısal momentum; skaler ve vektör bileşenleri.

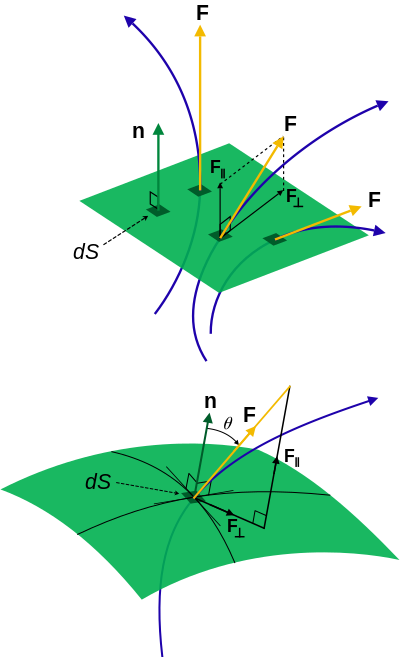
Örnekler

Elektrik akımı yoğunluğu, tüm bu yöntemleri kapsayan bir örnektir. Açısal momentum hesap gerektirmeyen bir örnektir. Sağdaki isimlendirme ve diyagramlar için aşağıdaki klasik mekanik bölümüne bakın.

Temel cebir

İşlemler basitçe çarpma ve bölmedir. Denklemler, her ikisi de elbette eşdeğer olan bir çarpım veya bölüm biçiminde yazılabilir.

	Açısal momentum	Elektrik akımı yoğunluğu
Bölüm formu	${ displaystyle p = { frac {L} {r}} , !}$	${ displaystyle J = { frac {I} {A}} , !}$
Ürün formu	${ displaystyle L = pr , !}$	${ displaystyle I = JA , !}$

Vektör cebiri

Bir vektörü bir vektöre bölmenin bir yolu yoktur, bu nedenle çarpım veya bölüm formları yoktur.

	Açısal momentum	Elektrik akımı yoğunluğu
Bölüm formu	Yok	${ displaystyle mathbf {J} cdot mathbf { hat {n}} = { frac {I} {A}} , !}$
Ürün formu	Den başlayarak ${ displaystyle L = pr, , !}$ dan beri L = 0 ne zaman p ve r vardır paralel veya antiparalel ve dik olduğunda bir maksimumdur, böylece tek bileşen p katkıda bulunan L teğetseldir |p| günah θ, açısal momentumun büyüklüğü L olarak yeniden yazılmalıdır ${ displaystyle L = pr sin theta. , !}$ Dan beri r, p ve L sağ üçlü oluşturursa, bu vektör formuna götürür ${ displaystyle mathbf {L} = mathbf {r} times mathbf {p}. , !}$	${ displaystyle mathbf {J} cdot mathbf { hat {n}} A = I, , !}$ ${ displaystyle mathbf {J} cdot mathbf {A} = I, , !}$

Temel hesap

Aritmetik işlemler, sınırlayıcı farklılaşma ve entegrasyon durumlarına göre değiştirilir. Denklemler bu eşdeğer ve alternatif yollarla ifade edilebilir.

	Mevcut yoğunluk
Diferansiyel form	${ displaystyle J = lim _ {A rightarrow 0} { frac {I} {A}} = { frac { mathrm {d} I} { mathrm {d} A}} , !}$
İntegral formu	${ displaystyle I = lim _ {A_ {i} rightarrow 0} sum _ {i} JA_ {i} = int _ {S} J { mathrm {d} A} , !}$ D neredeBir anlamına gelir diferansiyel alan öğesi (Ayrıca bakınız yüzey integrali ). Alternatif olarak integral formu için ${ displaystyle mathrm {d} I = J { mathrm {d} A}, , !}$ ${ displaystyle I = int _ {S} J { mathrm {d} A}. , !}$

Vektör hesabı

	Mevcut yoğunluk
Diferansiyel form	${ displaystyle mathbf {J} cdot mathbf { hat {n}} = { frac { mathrm {d} I} { mathrm {d} A}} , !}$
İntegral formu	${ displaystyle I = int _ {S} mathbf {J} cdot mathrm {d} mathbf {A} , !}$ D neredeBir = ndBir diferansiyel mi vektör alanı.

Tensör analizi

Vektörler rank-1'dir tensörler. Aşağıdaki formüller, tensörlerin dilindeki vektör denklemlerinden fazlası değildir.

	Açısal momentum	Elektrik akımı yoğunluğu
Diferansiyel form	Yok	${ displaystyle J_ {i} n_ {i} = { frac { mathrm {d} I} { mathrm {d} A}} , !}$
Ürün / integral formu	Den başlayarak ${ displaystyle mathbf {L} = mathbf {r} times mathbf {p} , !}$ bileşenler Lben, rj, pben, nerede i, j, k her biri 1, 2, 3 değerlerini alan kukla endekslerdir. tensör analizinden kimlik ${ displaystyle mathbf {a} = mathbf {b} times mathbf {c}, quad a_ {i} = epsilon _ {ijk} b_ {j} c_ {k}, , !}$ nerede εijk ... permütasyon / Levi-Cita tensörü, sebep olur ${ displaystyle L_ {i} = epsilon _ {ijk} r_ {j} p_ {k}. , !}$	Kullanmak Einstein toplama kuralı, ${ displaystyle J_ {i} n_ {i} mathrm {d} A = mathrm {d} I , !}$ ${ displaystyle int _ {S} J_ {i} mathrm {d} A_ {i} = I , !}$

Çoktan seçmeli tanımlar

Bazen seçilen birimler sistemi içinde, bir veya daha fazla miktarı birden fazla şekilde tanımlama özgürlüğü vardır. Durum iki duruma ayrılır:^[6]

Birbirini dışlayan tanımlar: Bir miktarın diğerleri açısından tanımlanması için bir dizi olası seçenek vardır, ancak yalnızca biri kullanılabilir, diğerleri kullanılamaz. Bir tanım için birden fazla münhasır denklemin seçilmesi bir çelişkiye yol açar - bir denklem bir miktar talep edebilir X olmak tanımlı bir şekilde başka kullanmak miktar Y, başka bir denklem gerektirirken tersine çevirmek, Y kullanılarak tanımlanabilir X, ancak daha sonra başka bir denklem her ikisinin de kullanımını yanlışlayabilir X ve Y, ve benzeri. Karşılıklı anlaşmazlık, hangi denklemin hangi miktarı tanımladığını söylemeyi imkansız kılıyor.

Eşdeğer tanımlar: Fiziksel teorideki diğer denklemler ve yasalarla eşdeğer ve kendi kendine tutarlı olan denklemleri tanımlamak, basitçe farklı şekillerde yazılır.

Her durum için iki olasılık vardır:

Bir tanımlayıcı denklem - tanımlanmış bir miktar: Diğerleri açısından tek bir miktarı tanımlamak için tanımlayıcı bir denklem kullanılır.

Bir tanımlayıcı denklem - bir dizi tanımlanmış miktar: Tanımlayıcı bir denklem, bir takım miktarları diğerlerine göre tanımlamak için kullanılır. Tek bir tanımlayıcı denklem içermemelidir bir miktar tanımlama Diğer tüm içindeki miktarlar aynı denklemaksi takdirde çelişkiler yeniden ortaya çıkar. Tek bir denklemde tek bir miktarla tanımlandıkları için, tanımlanan miktarların ayrı bir tanımı yoktur. Ayrıca, tanımlanan miktarlar daha önce tanımlanmış olabilir, bu nedenle aynı denklemde başka bir miktar bunları tanımlıyorsa, tanımlar arasında bir çatışma olur.

Miktarları tanımlayarak çelişkiler önlenebilir art arda; sipariş hangi miktarların tanımlandığı dikkate alınmalıdır. Bu örnekleri kapsayan örnekler, elektromanyetizma ve aşağıda verilmiştir.

Diferansiyel manyetik kuvvet dF küçük bir şarj elemanı nedeniyle dq oluşturan elektrik akımı ben (Konvansiyonel akım kullanıldı). Kuvvet olmalı entegre hat vektöre göre akım akışı yolu boyunca satır öğesi dr.

Örnekler

Birbirini dışlayan tanımlar:

manyetik indüksiyon alanı B açısından tanımlanabilir elektrik şarjı q veya akım ben, ve Lorentz kuvveti (manyetik terim) F alan nedeniyle yük taşıyıcıların tecrübeli,

${ displaystyle { başlar {hizalı} mathbf {F} & = q sol ( mathbf {v} times mathbf {B} sağ) & = sol ( int I mathrm {d} t right) left ({ frac { mathrm {d} mathbf {r}} { mathrm {d} t}} times mathbf {B} right) & = left ( int I mathrm {d} t { frac { mathrm {d} mathbf {r}} { mathrm {d} t}} right) times mathbf {B} & = I left ( int mathrm {d} mathbf {r} right) times mathbf {B} & = I left ( mathbf {l} times mathbf {B} right), end {hizalı} } , !}$

nerede ${ displaystyle mathbf {l} = int mathrm {d} mathbf {r} , !}$ yük taşıyıcıları tarafından geçilen konumdaki değişiklik (akımın konumdan bağımsız olduğu varsayılırsa, öyle değilse akım yolu boyunca bir çizgi integrali yapılmalıdır) veya manyetik akı cinsinden Φ_B bir yüzeyden Salan skaler olarak kullanıldığında Bir ve vektör: ${ displaystyle mathbf {A} = A mathbf { hat {n}} , !}$ ve ${ displaystyle mathbf { hat {n}} , !}$ normal bir birimdir Birya farklı biçimde

${ displaystyle mathbf {B} cdot mathbf { hat {n}} = { frac { mathrm {d} Phi _ {B}} { mathrm {d} A}}, , ! }$

veya integral formu,

${ displaystyle mathbf {B} cdot mathbf { hat {n}} mathrm {d} A = mathrm {d} Phi _ {B}, , !}$

${ displaystyle Phi _ {B} = int _ {S} mathbf {B} cdot mathrm {d} mathbf {A}. , !}$

Ancak, yukarıdaki denklemlerden yalnızca biri, B aşağıdaki sebepten dolayı Bir, r, v, ve F başka bir yerde açık bir şekilde tanımlanmıştır (büyük olasılıkla mekanik ve Öklid geometrisi ).

Kuvvet denklemi tanımlarsa B, nerede q veya ben önceden tanımlanmışsa, akı denklemi Φ_B, dan beri B önceden açık bir şekilde tanımlanmıştır. Akı denklemi tanımlıyorsa B, nerede Φ_Bkuvvet denklemi için tanımlayıcı bir denklem olabilir ben veya q. Çelişkiye ne zaman dikkat edin B her iki denklem de tanımlar B aynı anda ve ne zaman B temel bir miktar değildir; kuvvet denklemi şunu gerektirir: q veya ben başka bir yerde tanımlanabilirken aynı zamanda akı denklemi şunu gerektirir: q veya ben kuvvet denklemi ile tanımlanabilir, benzer şekilde kuvvet denklemi requires gerektirir_B akı denklemi ile tanımlanmalıdır, aynı zamanda akı denklemi_B başka yerde tanımlanmıştır. Her iki denklemin aynı anda tanım olarak kullanılması için, B temel bir miktar olmalıdır, böylece F ve Φ_B kaynaklandığı tanımlanabilir B açık bir şekilde.^[6]

Eşdeğer tanımlar:

Başka bir örnek ise indüktans L Tanım olarak kullanılacak iki eşdeğer denklem içeren.^[7][8]

Açısından ben ve Φ_Bendüktans şu şekilde verilir:

${ displaystyle L = N { frac { mathrm {d} Phi _ {B}} { mathrm {d} I}}, , !}$

açısından ben ve indüklenmiş emf V

${ displaystyle V = -L { frac { mathrm {d} I} { mathrm {d} t}}. , !}$

Bu ikisi eşdeğerdir Faraday'ın indüksiyon yasası:

${ displaystyle V = -N { frac { mathrm {d} Phi _ {B}} { mathrm {d} t}}, , !}$

${ displaystyle V { mathrm {d} t} = - N mathrm {d} Phi _ {B}, , !}$

ilk tanımın yerine L

${ displaystyle L = -V { frac { mathrm {d} t} { mathrm {d} I}} , !}$

${ displaystyle V = -L { frac { mathrm {d} I} { mathrm {d} t}} , !}$

ve dolayısıyla birbirlerini dışlamazlar.

Bir tanımlayıcı denklem - bir dizi tanımlanmış miktar

Dikkat edin L tanımlayamıyorum ben ve Φ_B aynı anda - bu hiç mantıklı değil. ben, Φ_B ve V büyük olasılıkla tümü daha önce (Φ_B yukarıda akı denkleminde verilmiştir);

${ displaystyle V = { frac { mathrm {d} W} { mathrm {d} q}}, quad I = { frac { mathrm {d} q} { mathrm {d} t}} , , !}$

nerede W = ücretli iş q. Ayrıca, ikisinin de tanımı yoktur. ben veya Φ_B ayrı - çünkü L onları aynı denklemde tanımlamaktır.

Ancak, Lorentz kuvveti için elektromanyetik alan:^[9][10][11]

${ displaystyle mathbf {F} = q sol [ mathbf {E} + sol ( mathbf {v} times mathbf {B} sağ) sağ], , !}$

için tek bir tanımlayıcı denklem olarak Elektrik alanı E ve manyetik alan B izin verildiğinden E ve B yalnızca tek bir değişkenle tanımlanmaz, aynı zamanda üç; güç F, hız v ve şarj et q. Bu, izole edilmiş tanımlarla tutarlıdır. E ve B dan beri E kullanılarak tanımlanır F ve q:

${ displaystyle mathbf {E} = mathbf {F} / q. , !}$

ve B tarafından tanımlandı F, v, ve qyukarıda verildiği gibi.

Tanımların sınırlamaları

Tanımlar ve işlevler: Miktarların tanımlanması, tanımdakilerden farklı parametrelerin bir fonksiyonu olarak değişebilir. Tanımlayıcı bir denklem yalnızca tanımlanan miktarın nasıl hesaplanacağını tanımlar, olumsuz İşlev bir uygulamadan diğerine değişeceğinden, miktarın diğer parametrelerin bir işlevi olarak nasıl değiştiğini açıklayın. Tanımlanan miktar, diğer parametrelerin bir fonksiyonu olarak nasıl değişir? kurucu denklem veya denklemler, çünkü bir uygulamadan diğerine ve bir yaklaşımdan (veya basitleştirmeden) diğerine değişiklik gösterir.

Örnekler

Kütle yoğunluğu ρ kütle kullanılarak tanımlanır m ve hacim V tarafından ancak sıcaklığın bir fonksiyonu olarak değişebilir T ve baskı p, ρ = ρ(p, T)

açısal frekans ω nın-nin dalga yayılımı kullanılarak tanımlanır Sıklık (veya eşdeğer olarak zaman dilimi T) salınımın bir fonksiyonu olarak dalga sayısı k, ω = ω(k). Bu dağılım ilişkisi dalga yayılımı için.

iade katsayısı bir nesne için çarpışma, çarpışma noktasına göre ayrılma ve yaklaşma hızları kullanılarak tanımlanır, ancak söz konusu yüzeylerin doğasına bağlıdır.

Tanımlar ve teoremler: Denklemleri tanımlamakla genel veya türetilmiş sonuçlar, teoremler veya yasalar arasında çok önemli bir fark vardır. Denklemleri tanımlama yapmak değil Bulmak hiç bilgi fiziksel bir sistem hakkında, bir ölçümü diğerlerine göre yeniden ifade ederler. Öte yandan sonuçlar, teoremler ve yasalar yapmak sistemin diğer özellikleri verilen bir miktar için hesaplamayı temsil ettikleri ve değişkenler değiştikçe sistemin nasıl davrandığını açıkladıkları için az da olsa anlamlı bilgiler sağlarlar.

Örnekler

Yukarıda Ampere yasası için bir örnek verilmiştir. Bir diğeri için momentumun korunumu N₁ başlangıç ​​momentine sahip ilk parçacıklar p_ben nerede ben = 1, 2 ... N₁, ve N₂ son momentuma sahip son parçacıklar p_ben (bazı parçacıklar patlayabilir veya yapışabilir) j = 1, 2 ... N₂koruma denklemi şu şekildedir:

${ displaystyle sum _ {i} ^ {N_ {1}} mathbf {p} _ { rm {i}} = sum _ {j} ^ {N_ {2}} mathbf {p} _ { rm {j}} , !}$

Momentumun tanımını hız cinsinden kullanarak:

${ displaystyle mathbf {p} = m mathbf {v} , !}$

böylece her bir parçacık için:

${ displaystyle mathbf {p} _ { rm {i}} = m_ {i} mathbf {v} _ { rm {i}} , !}$ ve ${ displaystyle mathbf {p} _ { rm {j}} = m_ {j} mathbf {v} _ { rm {j}} , !}$

koruma denklemi şu şekilde yazılabilir:

${ displaystyle sum _ {i} ^ {N_ {1}} m_ {i} mathbf {v} _ { rm {i}} = sum _ {j} ^ {N_ {2}} m_ {i } mathbf {v} _ { rm {i}}. , !}$

Önceki versiyonla aynıdır. Tanımlar değiştirildiğinde nicelikler değiştirilerek hiçbir bilgi kaybolmaz veya kazanılmaz, ancak denklemin kendisi sistem hakkında bilgi verir.

Tek seferlik tanımlar

Tipik olarak bir türetme sonucu ortaya çıkan bazı denklemler, uygulama kapsamında tek seferlik bir tanım görevi gören faydalı miktarlar içerir.

Örnekler

İçinde Özel görelilik, göreceli kütle fizikçilerden destek ve olumsuzluk var.^[12] Şu şekilde tanımlanır:

${ displaystyle m = gamma m_ {0} , !}$

nerede m₀ ... dinlenme kütlesi nesnenin ve γ Lorentz faktörü. Bu, momentum gibi bazı miktarlar yapar p ve enerji E Göreli kütle kullanarak diğer denklemlerden elde edilmesi kolay, hareket halindeki büyük bir nesnenin:

${ displaystyle mathbf {p} = m mathbf {v} rightarrow mathbf {p} = gamma m_ {0} mathbf {v}}$

${ displaystyle E = mc ^ {2} rightarrow E = gamma m_ {0} c ^ {2}}$

Ancak bu değil her zaman uygulayın, örneğin kinetik enerji T ve güç F aynı nesnenin değil veren:

${ displaystyle T = { frac {m} {2}} mathbf {v} cdot mathbf {v} nrightarrow T = { frac { gamma m_ {0}} {2}} mathbf {v } cdot mathbf {v}}$

${ displaystyle mathbf {F} = m mathbf {a} nrightarrow mathbf {F} = gamma m_ {0} mathbf {a}}$

Lorentz faktörünün daha derin bir anlamı ve kaynağı vardır ve uygun zaman ve koordinat zamanı ile dört vektör. Yukarıdaki doğru denklemler, tanımların doğru sırayla uygulanmasının sonucudur.

Yüklü bir parçacığı saptıran manyetik alan, sözde tanımlayıcı manyetik sertlik parçacık için.

Elektromanyetizmada, bir yüklü parçacık (kütle m ve şarj et q) düzgün bir manyetik alanda B hızda dairesel bir sarmal yay içinde alan tarafından saptırılır v ve Eğri yarıçapı r, sarmal yörüngenin bir açıyla eğimli olduğu yer θ -e B. manyetik kuvvet ... merkezcil kuvvet yani kuvvet F parçacık üzerinde hareket etmek;

${ displaystyle mathbf {F} = - { frac {m sol ( mathbf {v} cdot { mathbf {v}} sağ) mathbf { hat {r}}} { sol | mathbf {r} right |}} = q left ( mathbf {v} times mathbf {B} sağ), , !}$

skaler forma indirgeme ve çözme |B||r|;

${ displaystyle { frac {m sol | mathbf {v} sağ | ^ {2}} { sol | mathbf {r} sağ |}} = q sol | mathbf {v} sağ | sol | mathbf {B} sağ | sin theta, , !}$

${ displaystyle { frac {m sol | mathbf {v} sağ |} { sol | mathbf {r} sağ |}} = q sol | mathbf {B} sağ | sin teta, , !}$

${ displaystyle sol | mathbf {B} sağ | sol | mathbf {r} sağ | = { frac {m sol | mathbf {v} sağ |} {q sin theta} }, , !}$

tanım olarak hizmet eder manyetik sertlik parçacığın.^[13] Bu, parçacığın kütlesine ve yüküne bağlı olduğundan, bir parçacığın bir B deneysel olarak ortaya çıkan alan kütle spektrometrisi ve parçacık dedektörleri.

Ayrıca bakınız

• Bünye denklemi
• Denklemi tanımlama (fiziksel kimya)
• Elektromanyetizma denklemlerinin listesi
• Klasik mekanikte denklemlerin listesi
• Akışkanlar mekaniğinde denklemlerin listesi
• Yerçekiminde denklemlerin listesi
• Nükleer ve parçacık fiziğinde denklemlerin listesi
• Kuantum mekaniğindeki denklemlerin listesi
• Fotonik denklemlerin listesi
• Göreli denklemlerin listesi
• Termodinamik denklemler tablosu

Dipnotlar

Kaynaklar

• P.M. Whelan; M.J. Hodgeson (1978). Fiziğin Temel Prensipleri (2. baskı). John Murray. ISBN  0-7195-3382-1.
• G. Woan (2010). Cambridge Fizik Formülleri El Kitabı. Cambridge University Press. ISBN  978-0-521-57507-2.
• A. Halpern (1988). 3000 Fizikte Çözülmüş Problemler, Schaum Serisi. Mc Graw Hill. ISBN  978-0-07-025734-4.
• R.G. Lerner; G.L. Trigg (2005). Fizik Ansiklopedisi (2. baskı). VHC Publishers, Hans Warlimont, Springer. sayfa 12–13. ISBN  978-0-07-025734-4.
• C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2. baskı). McGraw Hill. ISBN  0-07-051400-3.
• P.A. Tipler; G. Mosca (2008). Bilim Adamları ve Mühendisler İçin Fizik: Modern Fizikle (6. baskı). W.H. Freeman ve Co. ISBN  978-1-4292-0265-7.
• L.N. El; J.D. Finch (2008). Analitik Mekanik. Cambridge University Press. ISBN  978-0-521-57572-0.
• T.B. Arkill; CJ Millar (1974). Mekanik, Titreşimler ve Dalgalar. John Murray. ISBN  0-7195-2882-8.
• H.J. Pain (1983). Titreşimlerin ve Dalgaların Fiziği (3. baskı). John Wiley & Sons. ISBN  0-471-90182-2.
• J.R. Forshaw; A.G. Smith (2009). Dinamik ve Görelilik. Wiley. ISBN  978-0-470-01460-8.
• G.A.G. Bennet (1974). Elektrik ve Modern Fizik (2. baskı). Edward Arnold (İngiltere). ISBN  0-7131-2459-8.
• DIR-DİR. Hibe; W.R. Phillips; Manchester Fiziği (2008). Elektromanyetizma (2. baskı). John Wiley & Sons. ISBN  978-0-471-92712-9.
• D.J. Griffiths (2007). Elektrodinamiğe Giriş (3. baskı). Pearson Education, Dorling Kindersley. ISBN  81-7758-293-3.

daha fazla okuma

• L.H. Greenberg (1978). Modern Uygulamalar ile Fizik. Holt-Saunders Uluslararası W.B. Saunders ve Co. ISBN  0-7216-4247-0.
• J.B. Marion; W.F. Hornyak (1984). Fizik Prensipleri. Holt-Saunders Uluslararası Saunders Koleji. ISBN  4-8337-0195-2.
• A. Beiser (1987). Modern Fizik Kavramları (4. baskı). McGraw-Hill (Uluslararası). ISBN  0-07-100144-1.
• H.D. Genç; R.A. Freedman (2008). Üniversite Fiziği - Modern Fizikle (12. baskı). Addison-Wesley (Pearson Uluslararası). ISBN  0-321-50130-6.