Karmaşık sayı - Complex number

Bir karmaşık sayı bir numara şeklinde ifade edilebilir a + bi, nerede a ve b vardır gerçek sayılar, ve ben temsil etmek hayali birim, denklemi tatmin etmek ben2 = −1. Çünkü bu denklemi hiçbir gerçek sayı karşılamaz, ben denir hayali numara. Karmaşık sayı için a + bi, a denir gerçek kısım, ve b denir hayali kısım. Karmaşık sayılar kümesi sembolü kullanılarak belirtilir . Tarihsel "hayali" terminolojisine rağmen, karmaşık sayılar matematik bilimlerinde gerçek sayılar kadar "gerçek" olarak kabul edilir ve doğal dünyanın bilimsel tanımının birçok yönünde temeldir.[not 1][1][2][3][4]
Karmaşık sayılar, gerçek sayılarda çözümü olmayan belirli denklemlerin çözümlerine izin verir. Örneğin denklem
gerçek bir sayının karesi negatif olamayacağı için gerçek bir çözümü yoktur. Ancak karmaşık sayılar bu soruna bir çözüm sağlar. Fikir, uzatmak ile gerçek sayılar belirsiz ben (bazen hayali birim olarak adlandırılır) ilişkiyi tatmin etmek için alınır ben2 = −1, böylece önceki gibi denklemlere çözümler bulunabilir. Bu durumda çözümler −1 + 3ben ve −1 − 3bengerçeği kullanılarak doğrulanabileceği gibi ben2 = −1:
Göre cebirin temel teoremi, herşey polinom denklemler gerçek veya karmaşık katsayılar tek bir değişkende karmaşık sayılarda çözüme sahiptir. Buna karşılık, gerçek katsayılı bazı polinom denklemlerinin gerçek sayılarda çözümü yoktur. 16. yüzyıl İtalyan matematikçisi Gerolamo Cardano çözüm bulma girişimlerinde karmaşık sayıları tanıtma konusunda itibar kazanmıştır. kübik denklemler.[5]
Resmi olarak, karmaşık sayı sistemi şu şekilde tanımlanabilir: cebirsel uzantı sıradan gerçek sayıların hayali bir sayıya göre ben.[6] Bu, karmaşık sayıların değişkende polinomlar olarak eklenebileceği, çıkarılabileceği ve çarpılabileceği anlamına gelir. benkuralına göre ben2 = −1. Ayrıca, karmaşık sayılar sıfır olmayan karmaşık sayılara da bölünebilir.[3] Genel olarak, karmaşık sayı sistemi bir alan.
Geometrik olarak, karmaşık sayılar, tek boyutlu sayı doğrusu için iki boyutlu karmaşık düzlem, kullanarak yatay eksen gerçek kısım için ve dikey eksen hayali kısım için. Karmaşık sayı a + bi nokta ile tanımlanabilir (a, b) karmaşık düzlemde. Gerçek kısmı sıfır olan karmaşık bir sayının tamamen olduğu söylenir hayali ve bu sayıların noktaları karmaşık düzlemin dikey ekseninde bulunur. Benzer şekilde, sanal kısmı sıfır olan karmaşık bir sayı, noktası karmaşık düzlemin yatay ekseninde bulunan gerçek bir sayı olarak görülebilir. Karmaşık sayılar, her bir karmaşık sayıyı orijinden uzaklığıyla (büyüklüğü) ilişkilendiren kutupsal formda da gösterilebilir ve belirli bir açı tartışma karmaşık sayının.
Karmaşık sayıların karmaşık düzlemle geometrik olarak tanımlanması; Öklid düzlemi (), yapılarını gerçek bir 2 boyutlu yapar vektör alanı belirgin. Karmaşık bir sayının gerçek ve sanal kısımları, kanonik sayıya göre bir vektörün bileşenleri olarak alınabilir. standart esas. Bu nedenle, karmaşık sayıların eklenmesi, vektörlerin olağan bileşen bazlı eklenmesi olarak hemen tasvir edilir. Bununla birlikte, karmaşık sayılar, bir vektör uzayında zorunlu olarak mevcut olmayan ek işlemler içeren daha zengin bir cebirsel yapıya izin verir. Örneğin, iki karmaşık sayının çarpımı her zaman yine karmaşık bir sayı verir ve aşağıdaki gibi vektörleri içeren olağan "ürünler" ile karıştırılmamalıdır. skaler çarpım, skaler çarpım veya diğer (sesqui) doğrusal formlar, birçok vektör alanında mevcuttur; ve geniş çapta sömürülenler vektör ürün sadece bir oryantasyon üç boyutlu bağımsız form.
Tanım

Karmaşık sayı, formun bir sayısıdır a + bi, nerede a ve b vardır gerçek sayılar, ve ben belirsiz bir tatmin edici ben2 = −1. Örneğin, 2 + 3ben karmaşık bir sayıdır.[7][3]
Bu şekilde, karmaşık bir sayı bir polinom tek belirsizde gerçek katsayılarla ben, bunun için ilişki ben2 + 1 = 0 empoze edilir. Bu tanıma dayanarak, karmaşık sayılar polinomlar için toplama ve çarpma kullanılarak toplanabilir ve çarpılabilir. İlişki ben2 + 1 = 0 eşitlikleri teşvik eder ben4k = 1, ben4k+1 = ben, ben4k+2 = −1, ve ben4k+3 = −ben, tüm tam sayılar için tutulan k; bunlar, karmaşık sayıların eklenmesi ve çarpılmasından kaynaklanan herhangi bir polinomun, doğrusal bir polinoma indirgenmesine izin verir. ben, yine formda a + bi gerçek katsayılarla a, b.
Gerçek sayı a denir gerçek kısım karmaşık sayının a + bi; gerçek numara b denir hayali kısım. Vurgulamak gerekirse, hayali kısım bir faktör içermiyor ben; yani hayali kısım b, değil bi.[8][9][3]
Resmi olarak, karmaşık sayılar şu şekilde tanımlanır: bölüm halkası of polinom halkası belirsiz olarak bentarafından ideal polinom tarafından oluşturulan ben2 + 1 (görmek altında ).[6]
Gösterim
Gerçek bir sayı a karmaşık bir sayı olarak kabul edilebilir a + 0ben, hayali kısmı 0 olan hayali numara bi karmaşık bir sayıdır 0 + bi, gerçek kısmı sıfır olan. Polinomlarda olduğu gibi, yazmak yaygındır a için a + 0ben ve bi için 0 + bi. Üstelik hayali kısım olumsuz olduğunda, yani b = −| b | < 0, yazmak yaygındır a − | b | i onun yerine a + (−| b |)ben; örneğin, b = −4, 3 − 4ben yerine yazılabilir 3 + (−4)ben.
Belirsizin çarpımından beri ben ve bir gerçek, gerçek katsayıları olan polinomlarda değişmeli, polinom a + bi olarak yazılabilir a + ib. Bu genellikle ifadelerle gösterilen hayali parçalar için uygundur, örneğin, b bir radikaldir.[10]
Karmaşık bir sayının gerçek kısmı z ile gösterilir Yeniden(z) veya ℜ (z); karmaşık bir sayının hayali kısmı z ile gösterilir Ben(z) veya ℑ (z).[1] Örneğin,
- ve
Ayarlamak tüm karmaşık sayılar ile gösterilir (dik kalın) veya (tahta kalın ).[1]
Bazı disiplinlerde, özellikle elektromanyetizma ve elektrik Mühendisliği, j yerine kullanılır ben gibi ben temsil etmek için sıklıkla kullanılır elektrik akımı.[11] Bu durumlarda, karmaşık sayılar şu şekilde yazılır: a + bjveya a + jb.
Görselleştirme
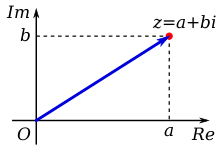
Karmaşık bir sayı z böylece bir ile tanımlanabilir sıralı çift (Yeniden(z), Ben(z)) iki boyutlu uzayda bir noktanın koordinatları olarak yorumlanabilen gerçek sayılar. En yakın alan, uygun koordinatlara sahip Öklid düzlemidir ve daha sonra karmaşık düzlem veya Argand diyagramı,[12][13][14] adını Jean-Robert Argand. Koordinatların yansıtılabileceği bir diğer önemli alan, bir kürenin iki boyutlu yüzeyidir ve daha sonra adı Riemann küresi.
Kartezyen karmaşık düzlem
İki rastgele gerçek değeri içeren karmaşık sayıların tanımı, hemen karmaşık düzlemde Kartezyen koordinatların kullanılmasını önerir. Yatay (gerçek) eksen genellikle sağa doğru artan değerler ile gerçek parçayı görüntülemek için kullanılır ve hayali parça dikey (hayali) ekseni, artan değerler ile.
Çizelgeli bir sayı, koordinatlanmış nokta olarak veya bir vektör pozisyonu kökeninden bu noktaya. Karmaşık bir sayının koordinat değerleri z dolayısıyla ifade edilebilir Kartezyen, dikdörtgenveya cebirsel form.
Özellikle, toplama ve çarpma işlemleri, karmaşık sayılar konum vektörleri olarak görüldüğünde çok doğal bir geometrik karakter alır: toplama, Vektör ilavesi, çarpma sırasında (bkz. altında ) büyüklüklerini çarpmaya ve yaptıkları açıları gerçek eksenle toplamaya karşılık gelir. Bu şekilde bakıldığında, karmaşık bir sayının çarpımı ben pozisyon vektörünü döndürmeye karşılık gelir saat yönünün tersine çeyreklik dönüş (90° ) kökeni hakkında - cebirsel olarak aşağıdaki gibi ifade edilebilen bir gerçek:
Kutupsal karmaşık düzlem

Modül ve argüman
Karmaşık düzlemdeki koordinatlar için alternatif bir seçenek, kutupsal koordinat sistemi noktanın mesafesini kullanan z -den Menşei (Ö) ve arasındaki açı pozitif gerçek eksen ve çizgi parçası Oz saat yönünün tersine bir anlamda. Bu, karmaşık sayıların kutupsal biçimine götürür.
mutlak değer (veya modül veya büyüklük) karmaşık bir sayı z = x + yi dır-dir[15]
Eğer z gerçek bir sayıdır (yani y = 0), sonra r = |x|. Yani, gerçek bir sayının mutlak değeri, bir karmaşık sayı olarak mutlak değerine eşittir.
Tarafından Pisagor teoremi, karmaşık bir sayının mutlak değeri, içindeki karmaşık sayıyı temsil eden noktanın başlangıcına olan mesafedir. karmaşık düzlem.
tartışma nın-nin z (birçok uygulamada "aşama" olarak anılır φ)[14] açısı yarıçap Oz pozitif gerçek eksenle ve şöyle yazılır . Modülusta olduğu gibi, argüman dikdörtgen formdan bulunabilir [16]- hayali gerçek parçaların bölümlerine ters teğet uygulayarak. Yarım açılı bir özdeşlik kullanarak, arktanın tek bir dalı, arg-işlev, (−π, π]ve vaka bazında daha ince bir analizden kaçınır
Normalde, yukarıda verildiği gibi, ana değer aralıkta (−π, π] seçilmiş. Aralıktaki değerler [0, 2π) eklenerek elde edilir 2π- değer negatifse. Değeri φ olarak ifade edilir radyan Bu makalede. Herhangi bir tamsayı katı kadar artabilir 2π ve pozitif gerçek eksenin ışınları tarafından ve başlangıç noktasından geçerek görüldüğü gibi, yine de aynı açıyı verir. z. Bu nedenle, arg işlevi bazen şu şekilde kabul edilir: çok değerli. 0 karmaşık sayısı için kutup açısı belirsizdir, ancak 0 kutup açısının keyfi seçimi yaygındır.
Değeri φ sonucuna eşittir atan2:
Birlikte, r ve φ karmaşık sayıları temsil etmenin başka bir yolunu verin, kutup formu, modül ve bağımsız değişken kombinasyonu bir noktanın düzlem üzerindeki konumunu tam olarak belirlediğinden. Orijinal dikdörtgen koordinatların kutupsal formdan kurtarılması, adı verilen formülle yapılır. trigonometrik form
Kullanma Euler formülü bu şu şekilde yazılabilir
Kullanmak cis işlev, bu bazen olarak kısaltılır
İçinde açı notasyonu, sıklıkla kullanılır elektronik temsil etmek fazör genlik ile r ve faz φ, şu şekilde yazılmıştır[17]
Karmaşık grafikler

Görselleştirirken karmaşık fonksiyonlar hem karmaşık bir girdi hem de çıktı gereklidir. Her bir karmaşık sayı iki boyutta temsil edildiğinden, karmaşık bir işlevi görsel olarak grafiğe dökmek, bir dört boyutlu uzay, bu sadece projeksiyonlarda mümkündür. Bu nedenle, karmaşık işlevleri görselleştirmenin başka yolları tasarlanmıştır.
İçinde alan boyama çıktı boyutları sırasıyla renk ve parlaklık ile temsil edilir. Etki alanı olarak karmaşık düzlemdeki her nokta süslütipik olarak renk karmaşık sayının argümanını temsil eden ve parlaklık büyüklüğü temsil ediyor. Karanlık noktalar modülü sıfıra yakın gösterir, daha parlak noktalar başlangıç noktasından daha uzaktadır, derecelendirme süreksiz olabilir, ancak monoton olduğu varsayılır. Renkler genellikle aşağıdaki adımlarla değişir π/3 için 0 -e 2π kırmızı, sarı, yeşil, camgöbeği, maviden macentaya. Bu arazilere renk çarkı grafikleri. Bu, bilgileri kaybetmeden işlevleri görselleştirmenin basit bir yolunu sağlar. Resimde sıfırlar gösteriliyor ±1, (2+ben) ve kutuplar ±√−2−2ben.
Riemann yüzeyleri karmaşık işlevleri görselleştirmenin başka bir yoludur.[daha fazla açıklama gerekli ] Riemann yüzeyleri şu şekilde düşünülebilir: deformasyonlar karmaşık düzlemin; yatay eksenler gerçek ve sanal girdileri temsil ederken, tek dikey eksen yalnızca gerçek veya sanal çıktıyı temsil eder. Bununla birlikte, Riemann yüzeyleri, onları 180 derece döndürmek hayali çıktıyı gösterecek şekilde inşa edilmiştir ve bunun tersi de geçerlidir. Alan renklendirmesinin aksine, Riemann yüzeyleri çok değerli işlevler sevmek .
Tarih
Çözüm radikaller (olmadan trigonometrik fonksiyonlar ) genel kübik denklem kareköklerini içerir negatif sayılar üç kök de gerçek sayılar olduğunda, bu durum, rasyonel kök testi kübik ise indirgenemez (sözde casus irreducibilis ). Bu muamma İtalyan matematikçiyi yönlendirdi Gerolamo Cardano 1545 civarında karmaşık sayıları düşünmek,[18] onun anlayışı ilkel olsa da.
Genel polinomlar problemi üzerine yapılan çalışmalar, sonuçta cebirin temel teoremi karmaşık sayılarla her biri için bir çözüm olduğunu gösterir. polinom denklemi derece bir veya daha yüksek. Karmaşık sayılar böylece bir cebirsel olarak kapalı alan, herhangi bir polinom denkleminin bir kök.
Birçok matematikçi karmaşık sayıların gelişimine katkıda bulundu. Karmaşık sayıların toplama, çıkarma, çarpma ve kök çıkarma kuralları İtalyan matematikçi tarafından geliştirilmiştir. Rafael Bombelli.[19] Karmaşık sayılar için daha soyut bir biçimcilik İrlandalı matematikçi tarafından daha da geliştirildi William Rowan Hamilton, bu soyutlamayı teorisine genişleten kuaterniyonlar.[20]
En erken kısa süreli referans Karekök nın-nin negatif sayılar belki de çalışmasında meydana geldiği söylenebilir. Yunan matematikçi İskenderiye Kahramanı 1. yüzyılda AD nerede onun Stereometrica Görünüşe göre yanlışlıkla imkansız bir hacmin hacmini düşünüyor hüsran bir piramit terime varmak hesaplamalarında negatif miktarlar düşünülmemiş olsa da Helenistik matematik ve Hero, onu olumlu ile değiştirdi ().[21]
Karmaşık sayıları kendi başına bir konu olarak inceleme dürtüsü ilk olarak 16. yüzyılda ortaya çıktı. cebirsel çözümler kökleri için kübik ve çeyreklik polinomlar İtalyan matematikçiler tarafından keşfedildi (bkz. Niccolò Fontana Tartaglia, Gerolamo Cardano ). Yakında fark edildi (ama çok sonra kanıtlandı)[22] Bu formüllerin, kişi yalnızca gerçek çözümlerle ilgilense bile, bazen negatif sayıların kareköklerinin manipülasyonunu gerektirdiğini. Örnek olarak, Tartaglia'nın formun kübik denklemi için formülü [not 2] denklemin çözümünü verir x3 = x gibi
İlk bakışta bu çok saçma görünüyor. Bununla birlikte, karmaşık sayılarla biçimsel hesaplamalar, denklemin z3 = ben çözümleri var −ben, ve . Bunları sırayla ikame ederek Tartaglia'nın kübik formülünde ve basitleştirmede, biri 0, 1 ve −1'in çözümleri olarak x3 − x = 0. Elbette bu özel denklem görünürde çözülebilir, ancak kübik denklemleri gerçek köklerle çözmek için genel formüller kullanıldığında, daha sonra matematikçilerin titizlikle gösterdiği gibi,[22] karmaşık sayıların kullanımı kaçınılmaz. Rafael Bombelli kübik denklemlerin bu görünüşte paradoksal çözümlerini açıkça ele alan ilk kişi oldu ve bu sorunları çözmeye çalışan karmaşık aritmetik için kurallar geliştirdi.
Bu miktarlar için "hayali" terimi, René Descartes 1637'de, hayali doğasını vurgulamak için acı çekmesine rağmen[23]
[...] bazen sadece hayali, yani her denklemde söylediğim kadar çok kişi hayal edilebilir, ancak bazen hayal ettiğimizle eşleşen hiçbir miktar yoktur.([...] quelquefois seulement, c'est-à-dire que l'on peut toujours en imaginer que j'ai dit en chaque équation, mais qu'y n'y a quelquefois aucune quantité qui qui qui qui qui qui qui 'hayal edin.)
Başka bir kafa karışıklığı kaynağı da denklemin cebirsel özdeşlikle kaprisli bir şekilde tutarsız görünüyordu , negatif olmayan gerçek sayılar için geçerlidir a ve bve aynı zamanda karmaşık sayı hesaplamalarında da kullanılan a, b olumlu ve diğer olumsuz. Bu kimliğin (ve ilgili kimliğin yanlış kullanımı) ) her ikisi de olduğunda a ve b Euler bile olumsuzdur. Bu zorluk nihayetinde özel sembolün kullanılmasına yol açtı. ben yerine √−1 bu hataya karşı korunmak için.[kaynak belirtilmeli ] Öyle olsa bile, Euler öğrencilere karmaşık sayıları bugün yaptığımızdan çok daha önce tanıtmanın doğal olduğunu düşünüyordu. Temel cebir ders kitabında, Cebirin Elemanları, bu sayıları hemen hemen aynı anda tanıtıyor ve sonra bunları baştan sona doğal bir şekilde kullanıyor.
18. yüzyılda karmaşık sayılar daha geniş bir kullanım kazandı çünkü karmaşık ifadelerin biçimsel manipülasyonunun trigonometrik fonksiyonları içeren hesaplamaları basitleştirmek için kullanılabileceği fark edildi. Örneğin, 1730'da Abraham de Moivre Bir açının tamsayı katının trigonometrik fonksiyonlarını bu açının trigonometrik fonksiyonlarının güçleriyle ilişkilendiren karmaşık kimliklerin, onun adını taşıyan aşağıdaki iyi bilinen formülle basitçe yeniden ifade edilebileceğini kaydetti, de Moivre formülü:
1748'de Leonhard Euler daha ileri gitti ve elde etti Euler formülü nın-nin karmaşık analiz:[24]
resmi olarak kompleksi manipüle ederek güç serisi ve bu formülün herhangi bir trigonometrik kimliği çok daha basit üstel kimliklere indirgemek için kullanılabileceği gözlemlendi.
Karmaşık bir sayının karmaşık düzlemde bir nokta olduğu fikri (yukarıda ) ilk olarak tarafından tanımlandı Caspar Wessel 1799'da,[25] 1685 gibi erken bir tarihte Wallis'in Cebir İncelemesi.[26]
Wessel'in anısı Proceedings of the Kopenhag Akademisi ama büyük ölçüde fark edilmeden gitti. 1806'da Jean-Robert Argand bağımsız olarak karmaşık sayılar üzerine bir kitapçık yayınladı ve cebirin temel teoremi.[27] Carl Friedrich Gauss daha önce yayınlamıştı topolojik teoremin 1797'deki kanıtı, ancak "-1'in karekökünün gerçek metafiziği" hakkındaki şüphelerini dile getirdi.[28] 1831'e kadar bu şüphelerin üstesinden geldi ve uçaktaki noktalar olarak karmaşık sayılar üzerine tezini yayınladı.[29][30] büyük ölçüde modern gösterim ve terminoloji oluşturmak.
Eğer kişi daha önce bu konuyu yanlış bir bakış açısıyla düşündüyse ve bu nedenle gizemli bir karanlık bulduysa, bu büyük ölçüde beceriksiz terminolojiye atfedilebilir. +1, −1, √ − 1 pozitif, negatif veya hayali (veya hatta imkansız) birimler değil, bunun yerine doğrudan, ters veya yan birimler olarak adlandırılmasaydı, o zaman böyle karanlıktan neredeyse hiç bahsedilemezdi. - Gauss[29][30]
19. yüzyılın başında, diğer matematikçiler, karmaşık sayıların geometrik temsilini bağımsız olarak keşfettiler: Buée,[31][32] Mourey,[33] Warren,[34] Français ve kardeşi Bellavit.[35][36]
İngiliz matematikçi G.H. Hardy Gauss'un karmaşık sayıları 'gerçekten emin ve bilimsel bir şekilde' kullanan ilk matematikçi olduğunu belirtti. Niels Henrik Abel ve Carl Gustav Jacob Jacobi Gauss 1831 tarihli tezini yayınlamadan önce bunları mutlaka rutin olarak kullanıyorlardı.[37]
Augustin Louis Cauchy ve Bernhard Riemann temel fikirlerini bir araya getirdi karmaşık analiz Cauchy'nin davasında 1825 civarında başlayarak yüksek bir tamamlanma durumuna geldi.
Teoride kullanılan ortak terimler esas olarak kuruculardan kaynaklanmaktadır. Argand aradı yön faktörü, ve modül;[38] Cauchy (1821) aradı küçültülmüş form (l'ifade réduite)[39] ve görünüşe göre terimi tanıttı tartışma; Gauss kullanıldı ben için ,[40] terimi tanıttı karmaşık sayı için a + bi,[41] ve aradı a2 + b2 norm.[42] İfade yön katsayısı, genellikle için kullanılır Hankel'e (1867) bağlıdır,[43] ve mutlak değer, için modül Weierstrass nedeniyle.
Genel teori üzerine daha sonra klasik yazarlar şunları içerir: Richard Dedekind, Otto Hölder, Felix Klein, Henri Poincaré, Hermann Schwarz, Karl Weierstrass Ve bircok digerleri.
İlişkiler ve işlemler
Eşitlik
Karmaşık sayılar, gerçek sayılara benzer bir eşitlik tanımına sahiptir; iki karmaşık sayı ve eşittir ancak ve ancak hem gerçek hem de hayali kısımları eşittir, yani ve . Sıfır olmayan karmaşık sayılar kutup formu Eşittirler ancak ve ancak aynı büyüklüğe sahiplerse ve argümanları bir tam sayı katları kadar farklıysa 2π.
Sipariş verme
Gerçek sayıların aksine, karmaşık sayıların doğal bir sıralaması yoktur. Özellikle, karmaşık sayıların doğal olarak iki boyutlu bir düzlemde var olduğu düşünüldüğünden, doğrusal sıralama toplama ve çarpma ile uyumlu karmaşık sayılarda - karmaşık sayılar bir sıralı alan. Bunun nedeni, sıralı bir alandaki herhangi bir karenin en azından 0, fakat ben2 = −1.
Eşlenik

karmaşık eşlenik karmaşık sayının z = x + yi tarafından verilir x − yi. Ya ile gösterilir z veya z*.[44] Bu tekli işlem karmaşık sayılar üzerine sadece temel işlemleri toplama, çıkarma, çarpma ve bölme uygulanarak ifade edilemez.
Geometrik olarak, z ... "yansıma" nın-nin z gerçek eksen hakkında. İki kez çekim yapmak, orijinal karmaşık sayıyı verir
bu işlemi bir evrim. Yansıma, hem gerçek kısmını hem de büyüklüğünü bırakır. z değişmemiş, yani
- ve
Karmaşık bir sayının hayali kısmı ve argümanı z işaretlerini fiil çekimi altında değiştir
- ve
Argüman ve büyüklükle ilgili ayrıntılar için, şu bölüme bakın: Kutup formu.
Karmaşık bir sayının çarpımı ve eşleniği olarak bilinir mutlak kare. Her zaman pozitif bir gerçek sayıdır ve her birinin büyüklüğünün karesine eşittir:
Bu özellik, belirli bir paydanın eşleniğine göre kesirin hem payını hem de paydasını genişleterek, karmaşık paydalı bir kesri gerçek paydalı eşdeğer bir kesire dönüştürmek için kullanılabilir. Bu sürece bazen "rasyonelleştirme "paydanın" (son ifadedeki payda irrasyonel bir gerçek sayı olsa da), çünkü bir paydadaki basit ifadelerden kökleri çıkarma yöntemine benziyor.
Karmaşık bir sayının gerçek ve hayali kısımları z konjugasyon kullanılarak çıkarılabilir:
- ve
Dahası, karmaşık bir sayı, ancak ve ancak kendi eşleniğine eşitse gerçektir.
Konjugasyon, temel karmaşık aritmetik işlemleri dağıtır:
Konjugasyon da kullanılır ters geometri, bir çizgi hakkında olanlardan daha genel olan yansımaları inceleyen bir geometri dalı. İçinde elektrik devrelerinin ağ analizi karmaşık eşlenik, eşdeğer empedansı bulmada kullanılır. maksimum güç aktarım teoremi aranıyor.
Toplama ve çıkarma

İki karmaşık sayı ve en kolay katma zirvelerin gerçek ve hayali kısımlarını ayrı ayrı ekleyerek. Demek ki:
Benzer şekilde, çıkarma olarak yapılabilir
Karmaşık sayıların karmaşık düzlemde görselleştirilmesini kullanarak, ekleme aşağıdaki geometrik yoruma sahiptir: iki karmaşık sayının toplamı ve , karmaşık düzlemdeki noktalar olarak yorumlanan, bir paralelkenar üç köşeden ve etiketli okların noktaları ve (bir hatta olmadıkları sürece). Aynı şekilde, bu noktaları çağırarak paralelkenarın sırasıyla ve dördüncü noktası üçgenler ve vardır uyumlu. Negatiflerin eklenmesi dikkate alınarak çıkarma görselleştirmesi sağlanabilir. çıkarılan.
Çarpma işlemi
Gerçek kısımdan beri, hayali kısım ve belirsiz kısım ben karmaşık bir sayının tümü kendi içinde sayı olarak kabul edilir, iki karmaşık sayı ve kuralları altında çarpılır dağıtım özelliği, değişmeli özellikler ve tanımlayıcı özellik Aşağıdaki şekilde
Karşılıklı ve bölünme
Konjugasyonu kullanarak, karşılıklı sıfır olmayan karmaşık bir sayının z = x + yi her zaman parçalanabilir
dan beri sıfır olmayan ima ediyor ki sıfırdan büyüktür.
Bu, rastgele bir karmaşık sayının bir bölümünü ifade etmek için kullanılabilir sıfır olmayan karmaşık bir sayı ile gibi
Kutupsal formda çarpma ve bölme
Çarpma, bölme ve üs alma formülleri, Kartezyen koordinatlardaki karşılık gelen formüllerden kutupsal formda daha basittir. İki karmaşık sayı verildiğinde z1 = r1(çünkü φ1 + ben günah φ1) ve z2 = r2(çünkü φ2 + ben günah φ2)trigonometrik kimlikler nedeniyle
türetebiliriz
Başka bir deyişle, mutlak değerler çarpılır ve argümanlar, ürünün kutupsal şeklini vermek için eklenir. Örneğin, ile çarparak ben çeyreğe karşılık gelirdönüş saat yönünün tersine, geri verir ben2 = −1. Sağdaki resim, çarpımını gösterir.
Gerçek ve hayali kısmından beri 5 + 5ben eşittir, bu sayının argümanı 45 derece veya π / 4'tür ( radyan ). Öte yandan, kırmızı ve mavi üçgenlerin başlangıç noktasındaki açıların toplamıdır. Arctan Sırasıyla (1/3) ve arctan (1/2). Böylece formül
tutar. Olarak Arctan işlev, oldukça verimli bir şekilde yaklaşık olarak tahmin edilebilir, bunun gibi formüller - Makineye benzer formüller - yüksek hassasiyetli yaklaşımlar için kullanılır π.
Benzer şekilde, bölme verilir
Kare kök
Karekökleri a + bi (ile b ≠ 0) , nerede
ve
sgn nerede işaret işlevi. Bu kare alarak görülebilir elde etmek üzere a + bi.[45][46] Buraya denir modül nın-nin a + bive karekök işareti, negatif olmayan gerçek kısma sahip karekökü belirtir. ana karekök; Ayrıca nerede [47]
Üstel fonksiyon
üstel fonksiyon her karmaşık sayı için tanımlanabilir z tarafından güç serisi
sonsuza sahip olan yakınsama yarıçapı.
Değer 1 üstel fonksiyonun Euler numarası
Eğer z gerçektir, biri vardır Analitik devam bu eşitliğin her karmaşık değeri için genişletilmesine izin verir zve böylece karmaşık üstelemeyi temel ile tanımlamak için e gibi
Fonksiyonel denklem
Üstel fonksiyon, fonksiyonel denklemBu, her iki üyenin güç serisi genişlemesini karşılaştırarak veya uygulayarak kanıtlanabilir. analitik devam denklemin kısıtlanmasından gerçek argümanlara.
Euler formülü
Euler formülü herhangi bir gerçek sayı için x,
Fonksiyonel denklem şu anlama gelir, eğer x ve y gerçektir, biri vardır
ki bu üstel fonksiyonun gerçek ve hayali kısımlarına ayrıştırılmasıdır.
Üs alma
Eğer x > 0 gerçek ve z karmaşık, üs alma şu şekilde tanımlanır:
nerede ln doğal logaritmayı gösterir.
Bu formülü aşağıdaki karmaşık değerlere genişletmek doğal görünüyor: x, ancak karmaşık logaritmanın gerçekten bir fonksiyon değil, bir fonksiyon olmasından kaynaklanan bazı zorluklar vardır. çok değerli işlev.
Karmaşık logaritma
Gerçek durumda, doğal logaritma olarak tanımlanabilir ters üstel fonksiyonun. Bunu karmaşık alana genişletmek için Euler'in formülünden başlayabiliriz. Bu, karmaşık bir sayı ise z yazılmıştır kutup formu
sonra onun karmaşık logaritma olmalı
Bununla birlikte, kosinüs ve sinüs periyodik fonksiyonlar olduğundan, tam sayı katı 2π. değişmez z. Örneğin, yani ikisi de ve doğal logaritması için olası değerlerdir .
Bu nedenle, karmaşık logaritma şu şekilde tanımlanmalıdır: çok değerli işlev:
Alternatif olarak, bir dal kesimi gerçek bir işlevi tanımlamak için kullanılabilir. Eğer z negatif bir gerçek sayı değil, ana değer karmaşık logaritmanın% 'si ile elde edilir Bu bir analitik işlev negatif gerçek sayıların dışında, ancak herhangi bir negatif gerçek sayıda sürekli olan bir işleve uzatılamaz.
Bunu takip eder eğer z yukarıdaki gibidir ve eğer t başka bir karmaşık sayıdır, sonra üs alma birden çok değerli işlevdir
Tamsayı ve kesirli üsler

Önceki formülde, t bir tamsayıdır, bu durumda sinüs ve kosinüs bağımsızdır k. Böylece, üs n bir tam sayıdır, o zaman iyi tanımlanmıştır ve üs alma formülü, de Moivre formülü:
n ninci kökler karmaşık bir sayının z tarafından verilir
için 0 ≤ k ≤ n − 1. (Buraya olağan mı (olumlu) npozitif gerçek sayının. kökü r.) Sinüs ve kosinüs periyodik olduğundan, diğer tam sayı değerleri k başka değerler vermeyin.
İken npozitif bir gerçek sayının inci kökü r olarak seçildi pozitif gerçek Numara c doyurucu cn = r, belirli bir kompleksi ayırt etmenin doğal bir yolu yoktur nkarmaşık bir sayının inci kökü. bu yüzden ninci kök bir ndeğerli işlev nın-nin z. Bu, pozitif gerçek sayılar durumunun aksine, kişinin
sol taraf şunlardan oluştuğundan n değerler ve sağ taraf tek bir değerdir.
Özellikleri
Alan yapısı
Set C karmaşık sayıların alan.[48] Kısaca, bu şu gerçeklerin geçerli olduğu anlamına gelir: ilk olarak, herhangi iki karmaşık sayı eklenebilir ve başka bir karmaşık sayı elde etmek için çarpılabilir. İkincisi, herhangi bir karmaşık sayı için z, onun toplamaya göre ters −z aynı zamanda karmaşık bir sayıdır; ve üçüncüsü, sıfır olmayan her karmaşık sayının bir karşılıklı karmaşık sayı. Dahası, bu işlemler bir dizi kanunu karşılamaktadır, örneğin değişme herhangi iki karmaşık sayı için toplama ve çarpma z1 ve z2:
Bu iki yasa ve bir alandaki diğer gereksinimler, gerçek sayıların kendilerinin bir alan oluşturduğu gerçeği kullanılarak yukarıda verilen formüllerle kanıtlanabilir.
Gerçeklerin aksine, C değil sıralı alan yani bir ilişki tanımlamak mümkün değil z1 < z2 bu, toplama ve çarpma ile uyumludur. Aslında, herhangi bir sıralı alanda, herhangi bir öğenin karesi zorunlu olarak pozitiftir. ben2 = −1 varlığını engeller sipariş açık C.[49]
Matematiksel bir konu veya yapının temelindeki alan karmaşık sayılar alanıysa, konunun adı genellikle bu gerçeği yansıtacak şekilde değiştirilir. Örneğin: karmaşık analiz, karmaşık matris, karmaşık polinom ve karmaşık Lie cebiri.
Polinom denklemlerin çözümleri
Herhangi bir karmaşık sayı verildiğinde ( katsayılar ) a0, ..., andenklem
en az bir karmaşık çözüme sahiptir zdaha yüksek katsayılardan en az birinin a1, ..., an sıfır değildir.[50] Bu, cebirin temel teoremi, nın-nin Carl Friedrich Gauss ve Jean le Rond d'Alembert. Bu gerçek yüzünden, C denir cebirsel olarak kapalı alan. Bu mülk, rasyonel sayılar alanı Q (polinom x2 − 2 rasyonel bir kökü yoktur, çünkü √2 rasyonel bir sayı değildir) ne de gerçek sayılar R (polinom x2 + a için gerçek bir kökü yok a > 0kareden beri x herhangi bir gerçek sayı için pozitiftir x).
Bu teoremin çeşitli kanıtları vardır. Liouville teoremi veya topolojik gibi olanlar sargı numarası veya bir ispat kombinasyonu Galois teorisi ve herhangi bir gerçek polinomun garip derece en az bir gerçek köke sahiptir.
Bu gerçek nedeniyle, tutan teoremler cebirsel olarak kapalı herhangi bir alan için başvurmak C. Örneğin, herhangi bir boş olmayan kompleks Kare matris en az bir (karmaşık) özdeğer.
Cebirsel karakterizasyon
Alan C aşağıdaki üç özelliğe sahiptir: birincisi, karakteristik 0. This means that 1 + 1 + ⋯ + 1 ≠ 0 for any number of summands (all of which equal one). İkincisi, onun aşkınlık derecesi bitmiş Q, ana alan nın-nin C, sürekliliğin temel niteliği. Third, it is cebirsel olarak kapalı (yukarıyı görmek). It can be shown that any field having these properties is izomorf (as a field) to C. Örneğin, cebirsel kapanış nın-nin Qp also satisfies these three properties, so these two fields are isomorphic (as fields, but not as topological fields).[51] Ayrıca, C is isomorphic to the field of complex Puiseux serisi. However, specifying an isomorphism requires the seçim aksiyomu. Another consequence of this algebraic characterization is that C contains many proper subfields that are isomorphic to C.
Characterization as a topological field
The preceding characterization of C describes only the algebraic aspects of C. That is to say, the properties of yakınlık ve süreklilik, which matter in areas such as analiz ve topoloji, are not dealt with. The following description of C olarak topological field (that is, a field that is equipped with a topoloji, which allows the notion of convergence) does take into account the topological properties. C contains a subset P (namely the set of positive real numbers) of nonzero elements satisfying the following three conditions:
- P is closed under addition, multiplication and taking inverses.
- Eğer x ve y farklı unsurlarıdır P, then either x − y veya y − x içinde P.
- Eğer S is any nonempty subset of P, sonra S + P = x + P bazı x içinde C.
Dahası, C has a nontrivial dahil edici otomorfizm x ↦ x* (namely the complex conjugation), such that x x* içinde P for any nonzero x içinde C.
Herhangi bir alan F with these properties can be endowed with a topology by taking the sets B(x, p) = { y | p − (y − x)(y − x)* ∈ P } olarak temel, nerede x ranges over the field and p aralıklar P. With this topology F is isomorphic as a topolojik alan C.
Tek bağlı yerel olarak kompakt topological fields vardır R ve C. This gives another characterization of C as a topological field, since C ayırt edilebilir R because the nonzero complex numbers are bağlı, while the nonzero real numbers are not.[52]
Formal construction
Construction as ordered pairs
William Rowan Hamilton introduced the approach to define the set C karmaşık sayıların[53] set olarak R2 nın-nin sıralı çiftler (a, b) of real numbers, in which the following rules for addition and multiplication are imposed:[48]
It is then just a matter of notation to express (a, b) gibi a + bi.
Construction as a quotient field
Though this low-level construction does accurately describe the structure of the complex numbers, the following equivalent definition reveals the algebraic nature of C more immediately. This characterization relies on the notion of fields and polynomials. A field is a set endowed with addition, subtraction, multiplication and division operations that behave as is familiar from, say, rational numbers. Örneğin, distributive law
must hold for any three elements x, y ve z of a field. Set R of real numbers does form a field. Bir polinom p(X) gerçek ile katsayılar formun bir ifadesidir
nerede a0, ..., an gerçek sayılardır. The usual addition and multiplication of polynomials endows the set R[X] of all such polynomials with a yüzük yapı. Bu yüzüğe polinom halkası gerçek sayıların üzerinde.
The set of complex numbers is defined as the bölüm halkası R[X]/(X 2 + 1).[6] This extension field contains two square roots of −1, namely (the kosetler nın-nin) X ve −X, sırasıyla. (The cosets of) 1 ve X form a basis of R[X]/(X 2 + 1) as a real vektör alanı, which means that each element of the extension field can be uniquely written as a doğrusal kombinasyon in these two elements. Equivalently, elements of the extension field can be written as ordered pairs (a, b) gerçek sayılar. The quotient ring is a field, because X2 + 1 dır-dir indirgenemez bitmiş R, so the ideal it generates is maksimum.
The formulas for addition and multiplication in the ring R[X], modulo the relation X2 = −1, correspond to the formulas for addition and multiplication of complex numbers defined as ordered pairs. So the two definitions of the field C vardır izomorf (as fields).
Accepting that C is algebraically closed, since it is an cebirsel uzantı nın-nin R in this approach, C bu nedenle cebirsel kapanış nın-nin R.
Matrix representation of complex numbers
Karışık sayılar a + bi can also be represented by 2 × 2 matrisler that have the following form:
Here the entries a ve b gerçek sayılardır. The sum and product of two such matrices is again of this form, and the sum and product of complex numbers corresponds to the sum and ürün of such matrices, the product being:
The geometric description of the multiplication of complex numbers can also be expressed in terms of rotasyon matrisleri by using this correspondence between complex numbers and such matrices. Moreover, the square of the absolute value of a complex number expressed as a matrix is equal to the belirleyici of that matrix:
The conjugate karşılık gelir değiştirmek matrisin.
Though this representation of complex numbers with matrices is the most common, many other representations arise from matrices ondan başka that square to the negative of the kimlik matrisi. Şu makaleye bakın: 2 × 2 gerçek matrisler for other representations of complex numbers.
Karmaşık analiz

The study of functions of a complex variable is known as karmaşık analiz and has enormous practical use in Uygulamalı matematik as well as in other branches of mathematics. Often, the most natural proofs for statements in gerçek analiz ya da sayı teorisi employ techniques from complex analysis (see asal sayı teoremi Örneğin). Unlike real functions, which are commonly represented as two-dimensional graphs, complex functions have four-dimensional graphs and may usefully be illustrated by color-coding a üç boyutlu grafik to suggest four dimensions, or by animating the complex function's dynamic transformation of the complex plane.
Kavramları yakınsak seriler ve sürekli fonksiyonlar in (real) analysis have natural analogs in complex analysis. A sequence of complex numbers is said to yakınsamak if and only if its real and imaginary parts do. Bu eşdeğerdir (ε, δ)-definition of limits, where the absolute value of real numbers is replaced by the one of complex numbers. From a more abstract point of view, C, endowed with the metrik
tam mı metrik uzay, which notably includes the üçgen eşitsizliği
for any two complex numbers z1 ve z2.
Like in real analysis, this notion of convergence is used to construct a number of temel fonksiyonlar: üstel fonksiyon tecrübe zayrıca yazılmış ez, olarak tanımlanır sonsuz seriler
The series defining the real trigonometric functions sinüs ve kosinüs yanı sıra hiperbolik fonksiyonlar sinh and cosh, also carry over to complex arguments without change. For the other trigonometric and hyperbolic functions, such as teğet, things are slightly more complicated, as the defining series do not converge for all complex values. Therefore, one must define them either in terms of sine, cosine and exponential, or, equivalently, by using the method of analitik devam.
Euler formülü devletler:
herhangi bir gerçek sayı için φ, özellikle
Unlike in the situation of real numbers, there is an sonsuzluk of complex solutions z denklemin
herhangi bir karmaşık sayı için w ≠ 0. It can be shown that any such solution z - aranan complex logarithm nın-nin w – satisfies
where arg is the tartışma tanımlı yukarıda, and ln the (real) doğal logaritma. As arg is a çok değerli işlev, unique only up to a multiple of 2π, log is also multivalued. ana değer of log is often taken by restricting the imaginary part to the Aralık (−π, π].
Karmaşık üs alma zω olarak tanımlanır
and is multi-valued, except when bir tamsayıdır. İçin ω = 1 / n, for some natural number n, this recovers the non-uniqueness of nth roots mentioned above.
Complex numbers, unlike real numbers, do not in general satisfy the unmodified power and logarithm identities, particularly when naïvely treated as single-valued functions; görmek failure of power and logarithm identities. For example, they do not satisfy
Both sides of the equation are multivalued by the definition of complex exponentiation given here, and the values on the left are a subset of those on the right.
Holomorfik fonksiyonlar
Bir işlev f : C → C denir holomorf tatmin ederse Cauchy-Riemann denklemleri. For example, any R-doğrusal harita C → C şeklinde yazılabilir
karmaşık katsayılarla a ve b. This map is holomorphic ancak ve ancak b = 0. The second summand is real-differentiable, but does not satisfy the Cauchy-Riemann denklemleri.
Complex analysis shows some features not apparent in real analysis. For example, any two holomorphic functions f ve g that agree on an arbitrarily small alt küme aç nın-nin C necessarily agree everywhere. Meromorfik fonksiyonlar, functions that can locally be written as f(z)/(z − z0)n with a holomorphic function f, still share some of the features of holomorphic functions. Other functions have essential singularities, gibi günah (1 /z) -de z = 0.
Başvurular
Complex numbers have applications in many scientific areas, including sinyal işleme, kontrol teorisi, elektromanyetizma, akışkan dinamiği, Kuantum mekaniği, haritacılık, ve vibration analysis. Some of these applications are described below.
Geometri
Şekiller
Üç non-collinear puan in the plane determine the şekil of the triangle . Locating the points in the complex plane, this shape of a triangle may be expressed by complex arithmetic as
The shape of a triangle will remain the same, when the complex plane is transformed by translation or dilation (by an afin dönüşüm ), corresponding to the intuitive notion of shape, and describing benzerlik. Thus each triangle içinde similarity class of triangles with the same shape.[54]
Fraktal geometri

Mandelbrot seti is a popular example of a fractal formed on the complex plane. It is defined by plotting every location where iterating the sequence değil uzaklaşmak ne zaman yinelenen infinitely. Benzer şekilde, Julia setleri have the same rules, except where sabit kalır.
üçgenler
Every triangle has a unique Steiner inellipse - bir elips inside the triangle and tangent to the midpoints of the three sides of the triangle. odaklar of a triangle's Steiner inellipse can be found as follows, according to Marden teoremi:[55][56] Denote the triangle's vertices in the complex plane as a = xBir + yBirben, b = xB + yBben, ve c = xC + yCben. Write the cubic equation , take its derivative, and equate the (quadratic) derivative to zero. Marden's Theorem says that the solutions of this equation are the complex numbers denoting the locations of the two foci of the Steiner inellipse.
Cebirsel sayı teorisi

As mentioned above, any nonconstant polynomial equation (in complex coefficients) has a solution in C. A fortiori, the same is true if the equation has rational coefficients. The roots of such equations are called cebirsel sayılar – they are a principal object of study in cebirsel sayı teorisi. Nazaran Q, the algebraic closure of Q, which also contains all algebraic numbers, C has the advantage of being easily understandable in geometric terms. In this way, algebraic methods can be used to study geometric questions and vice versa. With algebraic methods, more specifically applying the machinery of alan teorisi için sayı alanı kapsamak birliğin kökleri, it can be shown that it is not possible to construct a regular üçgen olmayan using only compass and straightedge – a purely geometric problem.
Başka bir örnek Gauss tamsayıları, that is, numbers of the form x + iy, nerede x ve y are integers, which can be used to classify sums of squares.
Analitik sayı teorisi
Analytic number theory studies numbers, often integers or rationals, by taking advantage of the fact that they can be regarded as complex numbers, in which analytic methods can be used. This is done by encoding number-theoretic information in complex-valued functions. Örneğin, Riemann zeta işlevi ζ(s) is related to the distribution of asal sayılar.
Yanlış integraller
In applied fields, complex numbers are often used to compute certain real-valued improper integrals, by means of complex-valued functions. Several methods exist to do this; görmek methods of contour integration.
Dinamik denklemler
İçinde diferansiyel denklemler, it is common to first find all complex roots r of karakteristik denklem bir doğrusal diferansiyel denklem or equation system and then attempt to solve the system in terms of base functions of the form f(t) = ert. Aynı şekilde fark denklemleri, the complex roots r of the characteristic equation of the difference equation system are used, to attempt to solve the system in terms of base functions of the form f(t) = rt.
In applied mathematics
Kontrol teorisi
İçinde kontrol teorisi, systems are often transformed from the zaman alanı için frekans alanı kullanmak Laplace dönüşümü. Sistemin sıfırlar ve kutuplar are then analyzed in the karmaşık düzlem. yol tarifi, Nyquist arsa, ve Nichols arsa techniques all make use of the complex plane.
In the root locus method, it is important whether zeros and poles are in the left or right half planes, that is, have real part greater than or less than zero. If a linear, time-invariant (LTI) system has poles that are
- in the right half plane, it will be kararsız,
- all in the left half plane, it will be kararlı,
- on the imaginary axis, it will have marjinal istikrar.
If a system has zeros in the right half plane, it is a nonminimum phase sistemi.
Signal analysis
Complex numbers are used in sinyal analizi and other fields for a convenient description for periodically varying signals. For given real functions representing actual physical quantities, often in terms of sines and cosines, corresponding complex functions are considered of which the real parts are the original quantities. Bir sinüs dalgası verilen Sıklık, the absolute value |z| karşılık gelen z ... genlik ve tartışma arg (z) ... evre.
Eğer Fourier analizi is employed to write a given real-valued signal as a sum of periodic functions, these periodic functions are often written as complex valued functions of the form
ve
where ω represents the açısal frekans ve karmaşık sayı Bir encodes the phase and amplitude as explained above.
This use is also extended into dijital sinyal işleme ve dijital görüntü işleme, which utilize digital versions of Fourier analysis (and dalgacık analysis) to transmit, kompres, restore, and otherwise process dijital ses signals, still images, and video sinyaller.
Another example, relevant to the two side bands of genlik modülasyonu of AM radio, is:
Fizikte
Electromagnetism and electrical engineering
İçinde elektrik Mühendisliği, Fourier dönüşümü is used to analyze varying voltajlar ve akımlar. Tedavisi dirençler, kapasitörler, ve indüktörler daha sonra, son ikisi için hayali, frekansa bağlı dirençler getirilerek ve üçünün tümü, adı verilen tek bir karmaşık sayı içinde birleştirilerek birleştirilebilir. iç direnç. Bu yaklaşıma fazör kalkülüs.
Elektrik mühendisliğinde hayali birim şu şekilde gösterilir: jile karışıklığı önlemek için ben, genellikle bunu belirtmek için kullanılır elektrik akımı veya daha özel olarak ben, genellikle anlık elektrik akımını belirtmek için kullanılır.
Beri Voltaj AC'de devre salınım yapıyor, şu şekilde temsil edilebilir:
Ölçülebilir miktarı elde etmek için gerçek kısım alınır:
Karmaşık değerli sinyal denir analitik gerçek değerli, ölçülebilir sinyalin temsili .[57]
Akışkan dinamiği
İçinde akışkan dinamiği, karmaşık işlevler açıklamak için kullanılır iki boyutta potansiyel akış.
Kuantum mekaniği
Karmaşık sayı alanı, kuantum mekaniğinin matematiksel formülasyonları nerede karmaşık Hilbert uzayları uygun ve belki de en standart olan böyle bir formülasyon için bağlam sağlar. Kuantum mekaniğinin orijinal temel formülleri - Schrödinger denklemi ve Heisenberg'in matris mekaniği - karmaşık sayılardan yararlanın.
Görelilik
İçinde özel ve Genel görelilik, metrik için bazı formüller boş zaman Uzay-zaman sürekliliğinin zaman bileşeninin hayali olması daha basit hale gelir. (Bu yaklaşım artık klasik görelilikte standart değildir, ancak temel bir şekilde kullanılır içinde kuantum alan teorisi.) Karmaşık sayılar, Spinors bir genellemedir tensörler görelilikte kullanılır.
Alanı genişletme süreci R gerçeklerin C olarak bilinir Cayley-Dickson inşaatı. Daha yüksek boyutlara taşınabilir ve kuaterniyonlar H ve sekizlik Ö (gerçek bir vektör uzayı olarak) sırasıyla 4 ve 8 boyutundadır. Bu bağlamda karmaşık sayılar olarak adlandırılmıştır. ikililer.[58]
Aynı inşaatın mülkiyeti gerçek olacak şekilde uygulanması gibi sipariş kaybolur, gerçek ve karmaşık sayılardan tanıdık özellikler her uzantı ile birlikte kaybolur. kuaterniyonlar değişme özelliğini kaybetmek, yani x·y ≠ y·x bazı kuaterniyonlar için x, yve çarpımı sekizlik, ayrıca değişmeli olmamasına ek olarak, ilişkisel olamaz: (x·y)·z ≠ x·(y·z) bazı oktonyonlar için x, y, z.
Gerçekler, karmaşık sayılar, kuaterniyonlar ve oktonyonların tümü normlu bölme cebirleri bitmiş R. Tarafından Hurwitz teoremi onlar sadece onlar; sedenyonlar Cayley-Dickson yapısının bir sonraki adımı olan bu yapıya sahip olunmaması.
Cayley-Dickson yapısı, düzenli temsil nın-nin Colarak düşündü R-cebir (bir R- çarpma ile vektör uzayı), temele göre (1, ben). Bu şu anlama gelir: R-doğrusal harita
bazı sabit karmaşık sayılar için w ile temsil edilebilir 2 × 2 matris (bir temel seçildikten sonra). Temeli ile ilgili olarak (1, ben), bu matris
yani, yukarıdaki karmaşık sayıların matris gösterimi ile ilgili bölümde bahsedilen. Bu bir doğrusal gösterim nın-nin C içinde 2 × 2 gerçek matrisler, tek değil. Herhangi bir matris
karesinin kimlik matrisinin negatifi olma özelliğine sahiptir: J2 = −ben. Sonra
ayrıca sahaya izomorfiktir Cve alternatif bir karmaşık yapı verir R2. Bu, a kavramı ile genelleştirilmiştir. doğrusal karmaşık yapı.
Hiper karmaşık sayılar ayrıca genellemek R, C, H, ve Ö. Örneğin, bu kavram, bölünmüş karmaşık sayılar halkanın unsurları olan R[x]/(x2 − 1) (aksine R[x]/(x2 + 1)). Bu halkada denklem a2 = 1 dört çözümü vardır.
Alan R tamamlanması Q, alanı rasyonel sayılar her zamanki gibi mutlak değer metrik. Diğer seçenekler ölçümler açık Q tarlalara götürmek Qp nın-nin p-adic sayılar (herhangi asal sayı p), dolayısıyla benzer olan R. Tamamlamanın başka önemli olmayan yolları yok Q -den R ve Qp, tarafından Ostrowski teoremi. Cebirsel kapanışlar nın-nin Qp hala bir norm taşıyor, ancak (aksine C) buna göre tam değil. Tamamlanma nın-nin cebirsel olarak kapalı olduğu ortaya çıktı. Bu alanın adı p-adik karmaşık sayılar.
Alanlar R ve Qp ve sonlu alan uzantıları dahil C, vardır yerel alanlar.
Ayrıca bakınız
- Cebirsel yüzey
- Karmaşık sayılar kullanan dairesel hareket
- Karmaşık tabanlı sistem
- Karmaşık geometri
- Çift karmaşık sayı
- Eisenstein tamsayı
- Euler'in kimliği
- Geometrik cebir (karmaşık düzlemi 2 boyutlu olarak içerir spinor alt uzay )
- Birliğin kökü
- Birim karmaşık numarası
Notlar
- ^ İlk şüphecilikten nihai kabule kadar tarihin kapsamlı bir açıklaması için bkz.Bourbaki 1998 ), sayfa 18-24.
- ^ Modern gösterimde Tartaglia'nın çözümü, iki küp kökü toplamının küpünü genişletmeye dayanmaktadır: İle , , , sen ve v açısından ifade edilebilir p ve q gibi ve , sırasıyla. Bu nedenle, . Ne zaman negatifse (casus irreducibilis), ikinci küp kökü, ilkinin karmaşık eşleniği olarak kabul edilmelidir.
Referanslar
- ^ a b c "Kapsamlı Cebir Sembolleri Listesi". Matematik Kasası. 25 Mart 2020. Alındı 12 Ağustos 2020.
- ^ Penrose, Roger (2016). Gerçeğe Giden Yol: Evren Yasalarına Eksiksiz Bir Kılavuz (yeniden basıldı.). Rasgele ev. s. 72–73. ISBN 978-1-4464-1820-8. P'nin özü. 73: "karmaşık sayılar, gerçekler kadar ve belki daha da fazlası, doğa ile gerçekten dikkate değer bir bütünlük bulur. Doğa, karmaşık sayı sisteminin kapsamı ve tutarlılığından bizler kadar etkilenmiş gibi, ve bu rakamlara, dünyasının en küçük ölçeklerinde kesin işlemlerini emanet etti. "
- ^ a b c d "Karışık sayılar". www.mathsisfun.com. Alındı 12 Ağustos 2020.
- ^ "Karmaşık Sayılar | Parlak Matematik ve Bilim Wiki". brilliant.org. Alındı 12 Ağustos 2020.
- ^ Burton, David M. (1995), Matematik Tarihi (3. baskı), New York: McGraw-Hill, s. 294, ISBN 978-0-07-009465-9
- ^ a b c Bourbaki, Nicolas. "VIII.1". Genel topoloji. Springer-Verlag.
- ^ Axler Sheldon (2010). Üniversite cebiri. Wiley. s.262.
- ^ Spiegel, M.R .; Lipschutz, S .; Schiller, J.J .; Spellman, D. (14 Nisan 2009), Karmaşık Değişkenler (2. Baskı), Schaum'un Anahat Serisi, McGraw Hill, ISBN 978-0-07-161569-3
- ^ Aufmann, Richard N .; Barker, Vernon C .; Ulus, Richard D. (2007), "Bölüm P", Üniversite Cebiri ve Trigonometri (6 ed.), Cengage Learning, s. 66, ISBN 978-0-618-82515-8
- ^ Görmek (Ahlfors 1979 ).
- ^ Brown, James Ward; Churchill, Ruel V. (1996), Karmaşık değişkenler ve uygulamalar (6. baskı), New York: McGraw-Hill, s. 2, ISBN 978-0-07-912147-9,
Elektrik mühendisliğinde mektup j yerine kullanılır ben.
- ^ Pedoe, Dan (1988), Geometri: Kapsamlı bir kurs, Dover, ISBN 978-0-486-65812-4
- ^ Görmek (Solomentsev 2001 ): "Noktaları $ C $ 'ın öğeleriyle tanımlanan $ R ^ 2 $ düzlemine karmaşık düzlem denir" ... "Karmaşık sayıların ve üzerlerindeki işlemlerin eksiksiz geometrik yorumu ilk olarak C'nin çalışmasında ortaya çıktı. Wessel (1799) Karmaşık sayıların geometrik temsili, bazen "Argand diyagramı" olarak da adlandırılır, Wessel'in bulgularını büyük ölçüde bağımsız bir şekilde yeniden keşfeden JR Argand'ın makalelerinin 1806 ve 1814 yıllarında yayınlanmasından sonra kullanıma girdi.
- ^ a b Weisstein, Eric W. "Karmaşık sayı". mathworld.wolfram.com. Alındı 12 Ağustos 2020.
- ^ Görmek (Apostol 1981 ), sayfa 18.
- ^ Kasana, H.S. (2005), "Bölüm 1", Karmaşık Değişkenler: Teori ve Uygulamalar (2. baskı), PHI Learning Pvt. Ltd, s. 14, ISBN 978-81-203-2641-5
- ^ Nilsson, James William; Riedel, Susan A. (2008), "Bölüm 9", Elektrik devreleri (8. baskı), Prentice Hall, s. 338, ISBN 978-0-13-198925-2
- ^ Kline, Morris. Matematiksel düşüncenin tarihi, cilt 1. s. 253.
- ^ Katz, Victor J. (2004), "9.1.4", Matematik Tarihi, Kısa Versiyon, Addison-Wesley, ISBN 978-0-321-16193-2
- ^ Hamilton, Wm. (1844). "Kuaterniyonlar teorisiyle bağlantılı yeni bir hayali nicelikler türü hakkında". İrlanda Kraliyet Akademisi Tutanakları. 2: 424–434.
- ^ Nahin, Paul J. (2007), Hayali Bir Hikaye: Hikayesi √−1, Princeton University Press, ISBN 978-0-691-12798-9, arşivlendi 12 Ekim 2012 tarihinde orjinalinden, alındı 20 Nisan 2011
- ^ a b Confalonieri, Sara (2015). Kübik Denklemler için Casus Irreducibilis'ten Kaçınmaya Yönelik Ulaşılamaz Girişim: Gerolamo Cardano'nun De Regula Aliza. Springer. s. 15–16 (not 26). ISBN 978-3658092757.
1843'te Pierre Laurent Wantzel, 1890'da Vincenzo Mollame, 1891'de Otto Hölder ve 1892'de Adolf Kneser tarafından denklemin üç gerçek, farklı köke sahip olduğu zaman, hayali sayıların kübik formülde mutlaka görünmesi gerektiği kanıtlanmıştır. Paolo Ruffini de sağladı. 1799'da eksik bir kanıt.
- ^ Descartes, René (1954) [1637], La Géométrie | René Descartes Geometrisi, ilk baskının bir kopyası ile, Dover Yayınları, ISBN 978-0-486-60068-0, alındı 20 Nisan 2011
- ^ Euler Leonard (1748). Analysin Infinitorum'da Giriş [Sonsuzun Analizine Giriş] (Latince). vol. 1. Lucerne, İsviçre: Marc Michel Bosquet & Co. s. 104.
- ^ Wessel, Caspar (1799). "Om Directionens analytiske Betegning, et Forsog, sphæriske Polygoners Oplosning ile düz bir düzlem için anvendt" [Yönün analitik temsilinde, özellikle düzlem ve küresel çokgenlerin belirlenmesine uygulanan bir çaba]. Nye Samling af det Kongelige Danske Videnskabernes Selskabs Skrifter [Danimarka Kraliyet Bilim Topluluğu'nun Yazılarının Yeni Koleksiyonu] (Danca). 5: 469–518.
- ^ Wallis, John (1685). Hem Tarihsel hem de Pratik Bir Cebir İncelemesi .... Londra, İngiltere: Richard Davis için John Playford tarafından basılmıştır. s. 264–273.
- ^ Argand (1806). Daha fazlasını görmek için tıklayınız. [Karmaşık büyüklükleri geometrik yapılarla temsil etmenin bir yolu üzerine bir deneme] (Fransızcada). Paris, Fransa: Madame Veuve Blanc.
- ^ Gauss, Carl Friedrich (1799) "Demonstratio nova theorematis omnem functionem cebebraicam rationalem integram unius variabilis in Faces reales primi vel secundi gradus resolvi posse." [Tek bir değişkenin herhangi bir rasyonel integral cebirsel fonksiyonunun birinci veya ikinci derece gerçek faktörlere dönüştürülebileceğine dair teoremin yeni kanıtı.] Ph.D. tezi, Helmstedt Üniversitesi, (Almanya). (Latince)
- ^ a b Gauss, C.F. (1831). "Anzeige von Theoria residuorum biquadraticorum, commentatio secunda" [Biquadratic kalıntılar teorisine dikkat edin, ikinci inceleme]. Göttingische gelehrte Anzeigen: 638.
- ^ a b Ewald, William B. (1996). Kant'tan Hilbert'e: Matematiğin Temellerinde Bir Kaynak Kitap. 1. Oxford University Press. s. 313. ISBN 9780198505358. Alındı 18 Mart 2020.
- ^ Adrien Quentin Buée (1745–1845): MacTutor
- ^ Buée (1806). "Immoire sur les quantités imaginaires" [Hayali büyüklükler üzerine anı]. Londra Kraliyet Cemiyeti'nin Felsefi İşlemleri (Fransızcada). 96: 23–88. doi:10.1098 / rstl.1806.0003. S2CID 110394048.
- ^ Mourey, C.V. (1861). Daha fazla nicelikler ve nicelikler imgelemleri ön plana çıkarır [Negatif nicelikler ve sözde hayali niceliklerin gerçek teorisi] (Fransızcada). Paris, Fransa: Mallet-Bachelier. 1861 1828 orijinal baskısı.
- ^ Görmek:
- Warren, John (1828). Negatif Miktarların Kare Köklerinin Geometrik Temsili Üzerine Bir İnceleme. Cambridge, İngiltere: Cambridge University Press.
- Warren, John (1829). "Negatif miktarların kareköklerinin geometrik temsiline karşı ileri sürülen itirazların değerlendirilmesi". Londra Kraliyet Cemiyeti'nin Felsefi İşlemleri. 119: 241–254. doi:10.1098 / rstl.1829.0022. S2CID 186211638.
- Warren, John (1829). "İndisleri negatif sayıların kareköklerini içeren niceliklerin kuvvetlerinin geometrik gösterimi üzerine". Londra Kraliyet Cemiyeti'nin Felsefi İşlemleri. 119: 339–359. doi:10.1098 / rstl.1829.0031. S2CID 125699726.
- ^ Français, J.F. (1813). "Nouveaux Principes de géométrie de position, et interprétation géométrique des symboles imaginaires" [Konum geometrisinin yeni ilkeleri ve karmaşık [sayı] sembollerinin geometrik yorumu]. Annales des mathématiques pures et aplike (Fransızcada). 4: 61–71.
- ^ Caparrini, Sandro (2000), "Karmaşık Sayıların Geometrik Yorumlanmasına İlişkin Bazı Çalışmaların Ortak Menşei Üzerine", Kim Williams'ta (ed.), İki Kültür, Birkhäuser, s. 139, ISBN 978-3-7643-7186-9 Sayfa 139'un özü Arşivlendi 2 Aralık 2016 Wayback Makinesi
- ^ Hardy, G.H .; Wright, E.M. (2000) [1938], Sayılar Teorisine Giriş, OUP Oxford, s. 189 (dördüncü baskı), ISBN 978-0-19-921986-5
- ^ Argand (1814). "Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la demonstration d'un theorème d'analise" [Yeni karmaşık sayılar teorisi üzerine düşünceler, ardından bir analiz teoreminin ispatına bir uygulama]. Annales de mathématiques pures ve aplikler (Fransızcada). 5: 197–209. S. 204, Argand karmaşık bir sayının modülünü tanımlar, ancak ona isim vermez: "Dans ce qui suit, les accens, indifféremment places, seront Empés pour indiquer la grandeur absolue des quantités qu'ils duygulu; ainsi, si , et étant réels, devra entender que'de ou ." (Aşağıda, nereye yerleştirilirse yerleştirilsin aksan işaretleri, atandıkları miktarların mutlak boyutunu belirtmek için kullanılacaktır; dolayısıyla , ve gerçek olmak, bunu anlamalı veya .)
S. 208, Argand, modül ve yön faktörü karmaşık bir sayının: " ... pourrait être appelé le modül de , ve yeniden mutlak büyüklük de la ligne , tandis que l'autre facteur, dont le module est l'unité, en représenterait la direction. " ( ... denilebilir modül nın-nin ve temsil ederdi mutlak boyut hattın [Not: Argand, karmaşık sayıları vektörler olarak temsil etti.], Diğer faktör [yani, modülü birlik olan [1], yönünü temsil eder.)
Ayrıca bakınız:- Jeff Miller (1999) Matematik Kelimelerinden Bazılarının Bilinen En Eski Kullanımları (M), İnternet Arşivi Wayback Makinesi
- ^ Cauchy, Augustin Louis (1821). Cours d'analyse de l'École royale politeknik (Fransızcada). vol. 1. Paris, Fransa: L'Imprimerie Royale. s. 183.
- ^ Gauss, C.F. (1831). "Theoria residuorum biquadraticorum. Commentatio secunda" [Biquadratic kalıntılar teorisi. İkinci anı.]. Yorumlar Societatis Regiae Scientiarum Gottingensis Recentiores (Latince). 7: 89–148. P. 96: "Quemadmodum scilicet arithmetica sublimior in quaestionibus hactenus pertractatis inter solo numeros integros reales versatur, ita theoremata circa residua biquadratica tunc tantum in summa simplicitate ac genuina venustate resplendent, quando campus arithmeticae ad quantitates Imaginarias extitur, ita ut absque resttione ipsius obiectum kurucu numeri formae a + bi, denotantibus ben, pro daha fazla Quantitatem imaginariam √ -1, atque a, b belirsiz omnes numeros reales integros inter - et +." (Elbette şimdiye kadar sadece gerçek tamsayı sayıları arasındaki problemlerde daha yüksek aritmetiğin araştırıldığı gibi, iki kadratik kalıntılarla ilgili teoremler de aritmetik alanı genişletilmiş olduğunda en büyük basitlik ve gerçek güzellikte parlar. hayali miktarları, böylece kısıtlama olmaksızın formun sayıları a + bi — ben konvansiyonel quantity -1 sanal niceliğini ve değişkenleri a, b arasındaki tüm gerçek tam sayıları [gösterir] ve + - bir nesne oluşturun.)
- ^ Gauss, C.F. (1831). "Theoria residuorum biquadraticorum. Commentatio secunda" [Biquadratic kalıntılar teorisi. İkinci anı.]. Yorumlar Societatis Regiae Scientiarum Gottingensis Recentiores (Latince). 7: 89–148. P. 96: "Masallar numeros kelime sayıları integros complexos, ita quidem, ut reales complexis rakipsiz, sed tamquam türleri onun kıta censeantur'unda." (Bu tür numaralara [yani, formun numaralarına a + bi ] "karmaşık tamsayı sayıları", böylece gerçek [sayılar] karmaşık [sayıların] zıttı olarak değil, içlerinde bulunan [sayıların] bir türü [olarak] kabul edilir.)
- ^ Gauss, C.F. (1831). "Theoria residuorum biquadraticorum. Commentatio secunda" [Biquadratic kalıntılar teorisi. İkinci anı.]. Yorumlar Societatis Regiae Scientiarum Gottingensis Recentiores (Latince). 7: 89–148. P. 98: "Productum numeri complexi per numerum ipsi conjunctum utriusque Normam kelime. Pro norma itaque numeri realis, ipsius quadratum habendum est. " (Bir "norm", karmaşık bir sayının çarpımı olarak adlandırılır [ör. a + ib ] eşleniği ile [a - ib ]. Bu nedenle, gerçek sayının karesi norm olarak kabul edilmelidir.)
- ^ Hankel, Hermann (1867). Vorlesungen über die complexen Zahlen und ihre Functionen [Karmaşık Sayılar ve İşlevleriyle İlgili Dersler] (Almanca'da). vol. 1. Leipzig, [Almanya]: Leopold Voss. s. 71. P. 71: "Wir werden den Factor (cos φ + i sin φ) haüfig den Richtungscoefficienten nennen. " (Çoğunlukla (cos φ + i sin φ) faktörüne "yön katsayısı" adını vereceğiz.)
- ^ Eski gösterim için bkz. (Apostol 1981 ), 15–16. sayfalar.
- ^ Abramowitz, Milton; Stegun, Irene A. (1964), Formüller, grafikler ve matematiksel tablolar içeren matematiksel işlevler el kitabı, Courier Dover Yayınları, s. 17, ISBN 978-0-486-61272-0, arşivlendi 23 Nisan 2016'daki orjinalinden, alındı 16 Şubat 2016, Bölüm 3.7.26, s. 17 Arşivlendi 10 Eylül 2009 Wayback Makinesi
- ^ Cooke Roger (2008), Klasik cebir: doğası, kökenleri ve kullanımları, John Wiley and Sons, s. 59, ISBN 978-0-470-25952-8, arşivlendi 24 Nisan 2016'daki orjinalinden, alındı 16 Şubat 2016, Çıkartma: sayfa 59 Arşivlendi 23 Nisan 2016 Wayback Makinesi
- ^ Görmek (Ahlfors 1979 ), sayfa 3.
- ^ a b Görmek (Apostol 1981 ), 15–16. sayfalar.
- ^ Görmek (Apostol 1981 ), sayfa 25.
- ^ Bourbaki, Nicolas. "VIII.1". Genel topoloji. Springer-Verlag.
- ^ Marker, David (1996), "Alanların Model Teorisine Giriş" Marker, D .; Messmer, M .; Pillay, A. (editörler), Alanların model teorisi, Mantıkta Ders Notları, 5, Berlin: Springer-Verlag, s. 1-37, ISBN 978-3-540-60741-0, BAY 1477154
- ^ Bourbaki, Nicolas. "VIII.4". Genel topoloji. Springer-Verlag.
- ^ Corry, Leo (2015). Sayıların Kısa Tarihi. Oxford University Press. s. 215–16.
- ^ Lester, J.A. (1994), "Üçgenler I: Şekiller", Aequationes Mathematicae, 52: 30–54, doi:10.1007 / BF01818325, S2CID 121095307
- ^ Kalman, Dan (2008a), "Marden'ın Teoreminin Temel Kanıtı", American Mathematical Monthly, 115 (4): 330–38, doi:10.1080/00029890.2008.11920532, ISSN 0002-9890, S2CID 13222698, arşivlendi 8 Mart 2012 tarihinde orjinalinden, alındı 1 Ocak 2012
- ^ Kalman, Dan (2008b), "Matematikteki En Harikulade Teorem", Online Matematik Dergisi ve Uygulamaları, arşivlendi 8 Şubat 2012 tarihinde orjinalinden, alındı 1 Ocak 2012
- ^ Grant, I.S .; Phillips, W.R. (2008), Elektromanyetizma (2 ed.), Manchester Physics Series, ISBN 978-0-471-92712-9
- ^ Kevin McCrimmon (2004) Ürdün Cebirlerinin Tadı, s. 64, Universitext, Springer ISBN 0-387-95447-3 BAY2014924
Çalışmalar alıntı
- Ahlfors, Lars (1979), Karmaşık analiz (3. baskı), McGraw-Hill, ISBN 978-0-07-000657-7
- Apostol, Tom (1981). Matematiksel analiz. Addison-Wesley.
- Solomentsev, E.D. (2001) [1994], "Karmaşık sayı", Matematik Ansiklopedisi, EMS Basın
daha fazla okuma
- Penrose, Roger (2005), Gerçeğe Giden Yol: Evren Yasalarına Eksiksiz Bir Kılavuz, Alfred A. Knopf, ISBN 978-0-679-45443-4
- Derbyshire, John (2006), Bilinmeyen Miktar: Cebirin Gerçek ve Hayali Bir Tarihi Joseph Henry Press, ISBN 978-0-309-09657-7
- Needham Tristan (1997), Görsel Karmaşık Analiz, Clarendon Press, ISBN 978-0-19-853447-1
Matematiksel
- Ahlfors, Lars (1979), Karmaşık analiz (3. baskı), McGraw-Hill, ISBN 978-0-07-000657-7
- Conway, John B. (1986), Bir Karmaşık Değişkenin Fonksiyonları ISpringer, ISBN 978-0-387-90328-6
- Joshi, Kapil D. (1989), Ayrık Matematiğin Temelleri, New York: John Wiley & Sons, ISBN 978-0-470-21152-6
- Pedoe, Dan (1988), Geometri: Kapsamlı bir kurs, Dover, ISBN 978-0-486-65812-4
- Basın, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Bölüm 5.5 Karmaşık Aritmetik", Sayısal Tarifler: Bilimsel Hesaplama Sanatı (3. baskı), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Solomentsev, E.D. (2001) [1994], "Karmaşık sayı", Matematik Ansiklopedisi, EMS Basın
Tarihi
- Bourbaki, Nicolas (1998), "Matematiğin Temelleri § mantığı: küme teorisi", Matematik tarihinin unsurları, Springer
- Burton, David M. (1995), Matematik Tarihi (3. baskı), New York: McGraw-Hill, ISBN 978-0-07-009465-9
- Katz Victor J. (2004), Matematik Tarihi, Kısa Versiyon, Addison-Wesley, ISBN 978-0-321-16193-2
- Nahin, Paul J. (1998), Hayali Bir Hikaye: Hikayesi , Princeton University Press, ISBN 978-0-691-02795-1
- Karmaşık sayıların tarihine ve karmaşık analizin başlangıcına hafif bir giriş.
- Ebbinghaus, H. D .; Hermes, H .; Hirzebruch, F .; Koecher, M .; Mainzer, K .; Neukirch, J .; Prestel, A .; Remmert, R. (1991), Sayılar (ciltli baskı), Springer, ISBN 978-0-387-97497-2
- Sayı kavramının tarihsel gelişimi üzerine gelişmiş bir bakış açısı.




































































































![{displaystyle z ^ {1 / n} = {sqrt [{n}] {r}} sol (cos left ({frac {varphi + 2kpi} {n}} ight) + isin left ({frac {varphi + 2kpi} {n}} ight) ight)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cc1b3406644f788c1ac1799d6328118ee66516f)
![{displaystyle {sqrt [{n}] {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10eb7386bd8efe4c5b5beafe05848fbd923e1413)



































![v (t) = mathrm {Re} (V) = mathrm {Re} sol [V_ {0} e ^ {jomega t} ight] = V_ {0} cos omega t.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66155dd3cd373aba4b6b5513fc702b0d6274408)










![sol (sqrt [3] {u} + sqrt [3] {v} ight) ^ 3 = 3 sqrt [3] {uv} left (sqrt [3] {u} + sqrt [3] {v} ight) + u + v](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d517dc90bb032850f746d46b44d566eceb0c6d7)
![x = sqrt [3] {u} + sqrt [3] {v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72653b7e905f735181aef73feeefd9829c3801f8)
![p = 3 sqrt [3] {uv}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e91ed0bfa159d0614caf741d557b8a700115eba3)



![x = sqrt [3] {q / 2 + sqrt {(q / 2) ^ 2- (p / 3) ^ 3}} + sqrt [3] {q / 2 - sqrt {(q / 2) ^ 2- (p / 3) ^ 3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4093f1a94136fbe89eca11f15c2ab50729537f0)


















