Bir elipsoid üzerinde jeodezik - Geodesics on an ellipsoid
| Jeodezi | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||||||||||||||||
Temel bilgiler | ||||||||||||||||||||||||||
Standartlar (tarih)
| ||||||||||||||||||||||||||

Çalışma bir elipsoid üzerinde jeodezik ile bağlantılı olarak ortaya çıktı jeodezi özellikle çözümü ile nirengi ağları.Dünya figürü yaklaşık olarak biryassı elipsoid, hafif düzleştirilmiş bir küre. Bir jeodezik eğimli bir yüzey üzerindeki iki nokta arasındaki en kısa yoldur, düz düz bir yüzeyde. Bir elipsoid üzerindeki bir nirengi ağının çözümü bu nedenle sferoidaltrigonometride bir dizi alıştırmadır (Euler 1755 ).
Dünya bir küre jeodeziklerharika çevreler (tümü kapalı) ve sorunlar toonları azaltır küresel trigonometri. Ancak, Newton (1687) Dünya'nın dönüşünün etkisinin, hafif basık bir elipsoide benzemesiyle sonuçlandığını gösterdi: bu durumda,ekvator ve meridyenler tek basit kapalı jeodeziktir. Ayrıca, ekvatordaki iki nokta arasındaki en kısa yol mutlaka ekvator boyunca ilerlemek zorunda değildir. Son olarak, eğer elipsoid, bir üç eksenli elipsoid (üç farklı yarı eksende), yalnızca üç jeodezik kapalıdır.
Jeodezik bir devrim elipsoidi üzerinde
Jeodezikleri tanımlamanın birkaç yolu vardır (Hilbert ve Cohn-Vossen 1952, s. 220–221). Basit bir tanım, bir yüzey üzerindeki iki nokta arasındaki en kısa yoldur. Bununla birlikte, onları sıfır olan yollar olarak tanımlamak genellikle daha kullanışlıdır.jeodezik eğrilik -Yani, analogu düz çizgiler keskin yüzeyde. Bu tanım, elipsoidin yüzeyinde o kadar uzağa seyahat eden jeodezikleri kapsar, böylece başlangıç noktasına geri dönmeye başlarlar, böylece diğer rotalar daha doğrudandır ve kendileriyle kesişen veya yeniden izleyen yolları içerir. Bir jeodeziğin yeterince kısa segmentleri, hala uç noktaları arasındaki en kısa rotadır, ancak jeodezikler mutlaka küresel olarak minimum değildir (yani, tüm olası yollar arasında en kısa). Küresel olarak en kısa yolların her biri jeodeziktir, ancak bunun tersi geçerli değildir.
18. yüzyılın sonunda, bir devrim elipsoidi (terimküremsi ayrıca kullanılır) iyi kabul edilen bir yaklaşımdıDünya figürü. Ayarı nirengi ağları tüm ölçümleri bir referans elipsoidi ve ortaya çıkan iki boyutlu problemi bir egzersiz insferoidal trigonometri olarak çözme (Bomford 1952, Çatlak. 3) (Leick vd. 2015, §4.5).

Çeşitli jeodezik problemleri iki tipten birine indirgemek mümkündür. İki noktayı düşünün: Bir -de enlemφ1 ve boylam λ1 veB enlemde φ2 ve boylamλ2 (bkz. Şekil 1). Bağlanan jeodezik ( Bir -e B) dır-dir AB, uzunluks12, hangisi azimutlar α1 veα2 iki uç noktada.[1] Genellikle ele alınan iki jeodezik problem şunlardır:
- doğrudan jeodezik problem veya ilk jeodezik problem, verilen Bir, α1, ve s12, belirlemek B ve α2;
- ters jeodezik problem veya ikinci jeodezik problem, verilen Bir ve B, belirlemek s12, α1, ve α2.
Şekil 1'den görülebileceği gibi, bu sorunlar üçgeni çözmeyi içerir.NAB bir açı verildiğinde, α1 doğrudan sorun için ve λ12 = λ2 - λ1 ters problem için ve onun iki komşu tarafı için. bir küre için bu problemlerin çözümleri basit alıştırmalardır.küresel trigonometri, kimin çözümü tarafından verilirküresel bir üçgeni çözmek için formüller. (Şu makaleye bakın: büyük çevre gezintisi.)
Bir devrim elipsoidi için, jeodeziği tanımlayan karakteristik sabit, Clairaut (1735). Jeodezik yolları için asistematik çözüm,Legendre (1806) veOriani (1806) (ve sonraki makaleler1808 ve1810 Doğrudan problem için tam çözüm (hesaplama tabloları ve çalışılmış bir örnek ile birlikte) Bessel (1825).
18. yüzyılda jeodezikler tipik olarak "en kısa hatlar" olarak anılırdı. "Jeodezik hat" terimi, Laplace (1799b):
Nous désignerons cette ligne sous le nom de Ligne géodésique [Bu hattı çağıracağız jeodezik çizgi].
Bu terminoloji İngilizceye ya "jeodezik çizgi" ya da "jeodezik çizgi" olarak tanıtıldı, örneğin (Hutton 1811 ),
Şimdi tarif ettiğimiz şekilde izlenen veya trigonometrik ölçülerden çıkarsanan bir çizgiye, belirttiğimiz yollarla denir. jeodezik veya jeodezik hat: yeryüzü üzerinde iki ucu arasına çekilebilecek en kısa olma özelliğine sahiptir; ve bu nedenle, bu iki nokta arasındaki mesafenin doğru yol ölçüsüdür.
Diğer alanlar tarafından benimsenmesinde jeodezik çizgisık sık jeodeziktercih edildi.
Bu bölüm problemi bir devrim elipsoidinde (hemoblat hem de prolat) ele almaktadır. Üç eksenli bir elipsoiddeki problem bir sonraki bölümde ele alınmaktadır.
Jeodezik için denklemler


Burada bir jeodezik için denklemler geliştirilir; türevini yakından takip eder Bessel (1825).Ürdün ve Eggert (1941),Bagratuni (1962), §15),Gan'shin (1967), Çatlak. 5),Krakiwsky ve Thomson (1974, §4),Rapp (1993), §1.2),Jekeli (2012), veBorre ve Strang (2012) ayrıca bu soruların türetmelerini de sağlar.
Ekvator yarıçaplı bir devrim elipsoidi düşününa ve kutupsal yarı eksen b. Düzleştirmeyi tanımlayın f = (a − b)/aeksantriklike = √a2 − b2/a = √f(2 − f)ve ikinci merkezlilik e′ = √a2 − b2/b = e/(1 − f). (Jeodezideki çoğu uygulamada, elipsoid basık olarak alınır,a > b; ancak teori, elipsoidleri prolate etmek için değişiklik yapılmadan uygulanır, a < b, bu durumda f, e2, ve e′2 olumsuz değildir.)
Elipsoid üzerindeki bir yolun temel parçasının uzunluğu olsunds. Figs'den. 2 ve 3, eğer onun azimutu ise α, sonra dsile ilgilidir dφ ve dλ tarafından
- (1)
nerede ρ ...meridyen eğrilik yarıçapı,R = ν cosφ enlem çemberinin yarıçapıdırφ, ve ν ...normal eğrilik yarıçapı Bu nedenle, temel segment tarafından verilir
veya
nerede φ ′ = dφ /dλ veLagrange işlevi L bağlıdırφ vasıtasıyla ρ (φ) veR(φ). Arasındaki keyfi bir yolun uzunluğu(φ1, λ1) ve (φ2, λ2) tarafından verildi
nerede φ bir fonksiyonudur λ doyurucuφ (λ1) = φ1 veφ (λ2) = φ2. Bu işlevi bulan en kısa yol veya jeodezik detaylar φ (λ) en aza indirens12. Bu bir alıştırmadırvaryasyonlar hesabı ve küçültme koşulu,Beltrami kimliği,
Yerine L ve Denklemleri kullanarak. (1) verir
Clairaut (1735) bunu buldum ilişki geometrik bir yapı kullanarak; benzer bir türetme tarafından sunulmaktadırLyusternik (1964), §10).[2] Bu ilişkinin farklılaştırılması,
Bu, Denklemler ile birlikte. (1), bir sisteme yol açaradi diferansiyel denklemler jeodezik için
İfade edebiliriz R açısındanparametrik enlem,β, kullanma
ve Clairaut'un ilişkisi daha sonra


Bu sinüs kuralı üçgenin iki tarafını ilişkilendiren küresel trigonometri NAB (bkz. Şekil 4), NA = 1⁄2π - β1, veNB = 1⁄2π - β2 ve zıt açılarıB = π - α2 ve Bir = α1.
Üçüncü tarafın ilişkisini bulmak içinAB = σ12, küresel yay uzunluğuve dahil açı N = ω12, küresel boylam, üçgeni dikkate almak faydalıdır NEP ekvatorda başlayan bir jeodezik; Şekil 5'e bakın. Bu şekilde, yardımcı küreye atıfta bulunulan değişkenler, parantez içinde gösterilen elipsoid için karşılık gelen miktarlarla gösterilmiştir. Alt simgesiz miktarlar, keyfi noktayı ifade eder.P; E, jeodeziğin ekvatoru kuzeye doğru kesiştiği nokta, kuzeye doğru başlangıç noktası olarak kullanılır.σ, s ve ω.
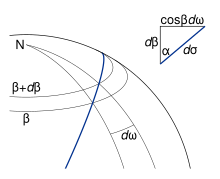
Eğer yan EP hareket ederek uzatılır P sonsuz derecede (bkz. Şekil 6)
- (2)
Denklemleri Birleştirme (1) ve (2) için diferansiyel denklemler verir s ve λ
Arasındaki ilişki β ve φ dır-dir
hangi verir
böylece jeodezik için diferansiyel denklemler
Son adım, kullanmaktır σ her iki diferansiyel denklemde bağımsız parametre olarak ve dolayısıyla ifade etmek için s veλ integraller olarak. Sinüs kuralını köşelere uygulamaE ve G küresel üçgendeEGP Şekil 5'te verir
nerede α0 azimut EBunu denklemin içine koymak ds/dσ ve sonucun bütünleştirilmesi
- (3)
nerede
ve integralin sınırları, böyleces(σ = 0) = 0. Legendre (1811), s. 180), denklemin s için denklemle aynıdırelips üzerinde yay yarı eksenli b√1 + e′2 çünkü2α0 veb. Denklemini ifade etmek içinλ açısından σ, Biz yazarız
aşağıdaki Denklem. (2) ve Clairaut ilişkisi.
- (4)
ve integrallerin sınırları seçilmiştir, öyle ki λ = λ0 ekvator geçidinde,σ = 0.
Bu yardımcı küreyi kullanarak bir jeodezik yolunun çözümünü tamamlar. Bu cihazla, büyük bir daire, bir devrim elipsoidi üzerindeki bir jeodezikle tam olarak eşleştirilebilir.
Bir karasal elipsoid üzerinde jeodezikleri yaklaştırmanın birkaç yolu da vardır (küçük düzleştirme ile) (Rapp 1991, §6); bunlardan bazıları şu konudaki makalede anlatılmıştır: coğrafi uzaklık Bununla birlikte, bunlar genellikle karmaşıklık açısından kesin çözüm yöntemiyle karşılaştırılabilir (Jekeli 2012, §2.1.4).
Jeodeziklerin davranışı



Şekil 7, eridiyanlar (yeşil) ve ekvatordan (kırmızı) oluşan basit kapalı jeodezikleri göstermektedir. (Burada "basit" niteliği, jeodeziğin kendi kendine kesişmeden kendi kendine kapanması anlamına gelir.) Bu, önceki bölümde verilen jeodezik denklemlerinden izler.
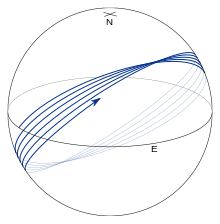
Diğer tüm jeodezikler, Şek. Ekvatorda başlayan jeodeziği gösteren 8 ve 9α0 = 45°. Ekvator çevresinde jeodezik salınımlar. Ekvator geçişlerine denir düğümler ve maksimum veya minimum enlem noktaları olarak adlandırılır köşeler; köşelerin parametrik enlemleri şu şekilde verilmiştir:β = ± (1⁄2π - | α0|)Jeodezik, boylam artmadan önce bir tam salınım enlemlamını tamamlar. 360°Böylece, ekvatorun her bir ardışık kuzeye geçişinde (bkz. Şekil 8), λ yaklaşık olarak tam bir ekvator devresine 2π f sinα0 (aprolate elipsoid için bu miktar negatiftir ve λtam bir devreden daha fazlasını tamamlar; bkz. Şekil 10). Neredeyse tüm değerler için α0jeodezik, elipsoidin iki tepe enlemi arasındaki o kısmını dolduracaktır (bakınız Şekil 9).


Elipsoid yeterince basık ise, yani,b⁄a < 1⁄2, başka bir basit kapalı jeodezik sınıfı mümkündür (Klingenberg 1982, §3.5.19). Bu tür iki jeodezik, Şek. 11 ve 12. Buradab⁄a = 2⁄7 ve ekvatoral azimut,α0yeşil (yani mavi) jeodezik, 53.175° (resp. 75.192°), böylece jeodezik, elipsoidin bir devresinde ekvator etrafında 2 tam salınımı tamamlar (sırasıyla 3).

Şekil 13, ortaya çıkan jeodezikleri (mavi olarak) gösterir.Bir ile α1 birden fazla15° en kısa yollar olmaktan çıktıkları noktaya kadar. (Düzleştirme,1⁄10 elipsoidal etkileri vurgulamak için.) Ayrıca (yeşil renkte) sabit eğriler gösterilmektedir. s12merkezlenmiş jeodezik çemberler Bir.Gauss (1828) herhangi bir yüzeyde jeodezik ve jeodezik çemberin dik açılarda kesiştiğini gösterdi. Kırmızı çizgiyeri kesmek, birden çok (bu durumda iki) en kısa jeodeziklere sahip noktaların konumu Bir. Bir küre üzerinde cutlocus bir noktadır. Yastıklı bir elipsoidde (burada gösterilmektedir), noktanın merkezindeki enlem çemberinin bir bölümüdür. zıt modlu -e Bir, φ = −φ1. Kesik yerinin uzunlamasına uzantısı yaklaşık olarakλ12 ∈ [π - f π cosφ1, π + f π cosφ1]. EğerBir ekvatorda yatıyor φ1 = 0, bu ilişki kesindir ve sonuç olarak ekvator yalnızca en kısa jeodeziktir.| λ12| ≤ (1 − f) π. Bir prolateellipsoid için, kesik lokus, anti-meridyenin bir kısmıdır ve nokta antipodal üzerinde merkezlenmiştir. Bir, λ12 = πve bu, karşıt noktaya ulaşılmadan önce meridyen jeodeziklerin en kısa yollar olmayı bıraktığı anlamına gelir.
Jeodeziklerin diferansiyel özellikleri
Jeodezikleri içeren çeşitli problemler, tedirgin olduklarında davranışlarını bilmeyi gerektirir. Bu, trigonometrik ayarlamalarda yararlıdır (Ehlert 1993 ), jeodezikleri takip eden sinyallerin fiziksel özelliklerinin belirlenmesi vb. Parametrelendirilmiş bir referans jeodezik düşünün sve ikinci bir jeodezik küçük bir mesafe t(s) ondan uzakta. Gauss (1828) bunu gösterdit(s) itaat ederGauss-Jacobi denklemi

nerede K(s) ... Gauss eğriliği -de sİkinci dereceden, doğrusal, homojen diferansiyel denklem olarak, çözümü iki bağımsız çözümün toplamı olarak ifade edilebilir.
nerede
Miktar m(s1, s2) = m12 sözdeazaltılmış uzunluk, ve M(s1, s2) = M12 ...jeodezik ölçek.[3]Temel tanımları Şekil 2'de gösterilmektedir. 14.
Bir devrim elipsoidi için Gauss eğriliği dır-dir
Helmert (1880), Denk. (6.5.1.)) Bu vaka için Gauss-Jacobiequation'ı çözerek m12 veM12 integraller olarak ifade edilecek.
Şekil 14'ten (üst alt şekil) gördüğümüz gibi, aynı noktadan başlayan iki jeodeziklerin, azimutlar ile birbirinden ayrılmasıdα1 dır-dir m12 dα1. Elipsoid gibi kapalı bir yüzeyde, m12 sıfıra yakın salınım. Hangi noktada m12 sıfır olan noktaeşlenik başlangıç noktasına. Jeodezik olmak için Bir ve B, uzunluks12, en kısa yol olması için Jacob koşulunu sağlamalıdır (Jacobi 1837 ) (Jacobi 1866, §6)(Forsyth 1927, §§26–27)(Bliss 1916 ), eşlenik bir nokta olmadığını Bir arasında Bir veB. Bu koşul karşılanmazsa, o zaman biryakınlarda daha kısa olan yol (jeodezik olması gerekmez). Dolayısıyla, Jacobi koşulu, jeodeziğin yerel bir özelliğidir ve jeodeziğin küresel en kısa yol olması için yalnızca gerekli koşuldur. Bir jeodeziğin en kısa yol olması için gerekli ve yeterli koşullar şunlardır:
- yassı bir elipsoid için, | σ12| ≤ π;
- prolat bir elipsoid için, | λ12| ≤ π, Eğer α0 ≠ 0; Eğer α0 = 0tamamlayıcı koşul m12 ≥ 0 eğer gerekli ise | λ12| = π.
Jeodezik zarfı
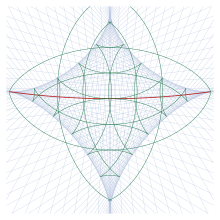

Belirli bir noktadan jeodezikler Bir devam ederse, kesilen lokusu Şekil 15'te gösterilen bir zarf oluşturacak şekilde yapıştırın. α1 katları3° açık mavi renkte gösterilmiştir. (Jeodezikler, ters noktaya yakın ilk geçişleri için gösterilir, sonraki geçişler için gösterilmez.) Bazı jeodezik daireler yeşil renkte gösterilir; bu formcusps zarfın üzerinde. Kesilen yer kırmızıyla gösterilmiştir. Zarf, eşlenik noktaların yeridir. Bir; zarfın üzerindeki noktalar, hangi noktanın bulunmasıyla hesaplanabilir.m12 = 0 jeodezik üzerinde.Jacobi (1891) zarfın ürettiği bu yıldız benzeri figüre astroid.
Astroidin dışında iki jeodezik her noktada kesişir; bu nedenle arasında iki jeodezik vardır (uzunluğu elipsoidin çevresinin yaklaşık yarısı kadar) Bir İki nokta arasındaki büyük bir çember üzerinde "kısa" ve "uzun" rotaların olduğu küre üzerindeki duruma karşılık gelir. Astroidin içinde her noktada dört jeodezik kesişir. Bu tür dört jeodezik, jeodeziklerin artan uzunluk sırasına göre numaralandırıldığı Şekil 16'da gösterilmiştir. (Bu şekil aynı pozisyonu kullanırBir Şekil 13'teki gibi ve aynı projeksiyonla çizilmiştir.) Daha kısa olan iki jeodezik kararlıyani m12 > 0, böylece daha kısa olan iki noktayı birbirine bağlayan yakın bir yol yoktur; diğer ikisi kararsız. Yalnızca en kısa satırda (ilk taş) σ12 ≤ π. Tüm jeodezikler, şekilde yeşil olarak gösterilen zarfa teğettir.
Astroid, (dış) gelişmek merkezde bulunan jeodezik dairelerin Bir. Aynı şekilde, jeodezik daireleriçerir astroid.
Jeodezik bir çokgenin alanı
Bir jeodezik çokgen kenarları jeodezik olan bir çokgendir. Şuna benzer küresel çokgen, yanları harika daireler. Böyle bir çokgenin alanı, ilk önce ageodesic segment ile ekvator arasındaki alan, yani dörtgen alanı hesaplanarak bulunabilir.AFHB Şekil 1'de (Danielsen 1989 ). Bu alan bilindikten sonra, bir çokgenin alanı, çokgenin tüm kenarlarından katkıların toplanmasıyla hesaplanabilir.
İşte bölge için bir ifade S12 nın-nin AFHBaşağıdaki geliştirildi Sjöberg (2006). Elipsoidin herhangi bir kapalı bölgesinin alanı,
nerede dT yüzey alanının bir unsurudur ve K... Gauss eğriliği. ŞimdiGauss-Bonnet teoremi jeodezik çokgen durumlarına uygulanan
nerede
jeodezik fazlalık ve θj dış açı atvertex j. Denklemi çarpmak Γtarafından R22, nerede R2 ...otantik yarıçap ve bunu denklemden çıkarmak T verir
nerede değeri K bir elipsoid için yerine geçmiştir.Bu formülün dörtgene uygulanması AFHB, not ederek Γ = α2 - α1ve integralin tamamlanması φ verir
integralin jeodezik çizginin üzerinde olduğu yerde (böylece φdolaylı olarak bir fonksiyonudur λİntegral, küçükler için geçerli bir dizi olarak ifade edilebilir. f(Danielsen 1989 ) (Karney 2013, §6 ve ek).
Jeodezik bir çokgenin alanı toplanarak verilir S12kenarlarının üzerinden. Bu sonuç, poligonun bir kutup içermemesi koşuluyla geçerlidir; Eğer yaparsa, 2π R22 tez eklenmelidir. Kenarlar köşeleriyle belirtilmişse, o zaman auygun ifade jeodezik fazlalık için E12 = α2 - α1 dır-dir
Doğrudan ve ters problemlerin çözümü
Jeodezik problemleri çözmek, jeodeziği yardımcı küre üzerine haritalandırmayı ve ilgili problemi çözmeyi gerektirir.büyük çevre gezintisi "Temel" küresel üçgeni çözerken NEP Şekil 5'te,Napier'in dörtgen üçgenler için kuralları istihdam edilebilir,
Jeodeziğin haritalanması, integrallerin mesafe için değerlendirilmesini içerir, sve boylam,λ, Denklemler. (3) ve (4) ve bunlar parametreye bağlıdır α0.
Doğrudan sorunu ele almak basittir, çünküα0 doğrudan verilen miktarlardan belirlenebilir φ1 ve α1.
Ters problem durumunda, λ12 verilir; bu, eşdeğer küresel açı ile kolayca ilişkilendirilemezω12 Çünkü α0 bilinmiyor. Bu nedenle, sorunun çözümü şunu gerektirir: α0 yinelemeli olarak bulundu.
Jeodezik uygulamalarda f küçüktür, integraller tipik olarak bir dizi olarak değerlendirilir (Legendre 1806 )(Oriani 1806 ) (Bessel 1825 ) (Helmert 1880 )(Rainsford 1955 ) (Rapp 1993 ). Keyfi içinf(3) ve (4) integralleri, sayısal dörtgen olarak veya bunları şu şekilde ifade ederek bulunabilir:eliptik integraller (Legendre 1806 ) (Cayley 1870 ).
Vincenty (1975) doğrudan ve ters sorunlar için çözümler sunar; bunlar, düzleştirmede üçüncü sıraya yapılan bir dizi genişletmeye dayanmaktadır ve yaklaşık olarak0.1 mm için WGS84 elipsoid; bununla birlikte, ters yöntem, neredeyse antipodal noktalar için yakınsama konusunda başarısız olur. Karney (2013) tam sağlamak için yeterli olan altıncı sıraya genişlemeleri sürdürüyorçift hassasiyet doğruluk|f| ≤ 1⁄50 ve ters problemin çözümünü her durumda birleşecek şekilde geliştirir.Karney (2013), ek), keyfi düzleştirme ile elipsoidlere uygulanabilen eliptikintegralleri kullanmak için yöntemi genişletir.
Üç eksenli bir elipsoid üzerinde jeodezik
Jeodezik problemi bir devrim elipsoidi için çözmek, matematiksel açıdan nispeten basittir: simetri nedeniyle jeodezikler sabit hareket Clairaut'un problemin indirgenmesine izin veren ilişkisi ile verildi.dördün. 19. yüzyılın başlarında (Legendre'nin çalışmasıyla, Oriani, Bessel, et al.), Jeodeziklerin özelliklerinin anelipsoid devriminde tam bir anlayış vardı.
Öte yandan, üç eksenli bir elipsoid (üç eşit olmayan eksenli) üzerindeki jeodezikler, hareketin açık bir sabitine sahip değildir ve bu nedenle 19. yüzyılın ilk yarısında çözülmemiş bir sorunu temsil eder. Dikkat çekici bir makalede, Jacobi (1839) hareketin bir kısmını keşfetti ve bu sorunun aynı zamanda dördüncüye indirgenmesine izin verdi (Klingenberg 1982, §3.5).[4]
Üç eksenli koordinat sistemi
İle tanımlanan elipsoidi düşünün
nerede (X,Y,Z) Kartezyen koordinatlar elipsoid üzerinde merkezlenmiştir ve genelliği kaybetmedena ≥ b ≥ c > 0.[5]Jacobi (1866), §§26–27) elipsoidal enlem ve Boylam(β, ω) tarafından tanımlandı

Sınırda b → a, βoblate elipsoid için parametrik enlem haline gelir, bu nedenle sembolün kullanımı β önceki bölümlerle uyumludur. Ancak, ω dır-dir farklı yukarıda tanımlanan küresel boylamdan.[6]
Sabit ızgara çizgileri β (mavi) veω (yeşil) Şekil 17'de verilmiştir. Bunlar bir dikey koordinat sistemi: ızgara çizgileri dik açılarda kesişir. Theellipsoid'in ana bölümleri X = 0 ve Z = 0 kırmızı olarak gösterilir. Üçüncü ana bölüm, Y = 0, hatlarla kaplıdır β = ± 90 ° ve ω = 0 ° veya±180°. Bu çizgiler dörtte buluşuyorgöbek noktaları (iki tanesi bu şekilde görülmektedir) neredeana eğrilik yarıçapları eşittir. Burada ve bu bölümdeki diğer şekillerde elipsoidin parametreleri a:b:c = 1.01:1:0.8ve yukarıdaki bir noktadan ortografik projeksiyonda görülüyor φ = 40 °,λ = 30 °.
Elipsoidal koordinatların ızgara çizgileri üç farklı şekilde yorumlanabilir:
- Elipsoid üzerindeki "eğrilik çizgileri" dir: bunlar ana eğriliğin yönlerine paraleldir (Monge 1796 ).
- Ayrıca elipsoidin kesişme noktalarıdır. bir ve iki yapraklı hiperboloidlerin konfokal sistemleri (Dupin 1813, 5.bölüm ).
- Son olarak, iki bitişik göbek noktası kullanılarak tanımlanan jeodezik elipsler ve hiperbollerdir (Hilbert ve Cohn-Vossen 1952, s. 188). Örneğin, sabit çizgiler β Şekil 17'de tanıdık bir şekilde oluşturulabilir elipsler için ip yapımı ipin uçları iki göbek noktasına tutturulmuş olarak.
Jacobi'nin çözümü
Jacobi, elipsoidal koordinatlarla ifade edilen jeodezik denklemlerin ayrılabilir olduğunu gösterdi. İşte arkadaşı ve komşusu Bessel'e keşfini şöyle anlattı (Jacobi 1839, Bessel'e Mektup),
Dünden önceki gün, jeodezik hatlar problemini bir üç eşit olmayan eksenli elipsoid. Dünyadaki en basit formüllerdir, Değişmeli integraller, 2 eksen eşit ayarlanırsa iyi bilinen eliptik integraller haline gelir.
Königsberg, 28 Aralık 38.
Jacobi'nin verdiği çözüm (Jacobi 1839 )(Jacobi 1866, §28)
Jacobi'nin belirttiği gibi "açının bir işlevi β açının eşit bir fonksiyonu ω. Bu iki fonksiyon sadece Abelyen integrallerdir ... "İki sabit δ veγ çözümde görünür. Tipikδ Eğer integrallerin alt sınırları jeodeziğin başlangıç noktası olarak kabul edilirse ve jeodeziklerin yönü şu şekilde belirlenirse sıfırdır γ. Bununla birlikte, göbek noktalarından başlayan jeodezikler için, γ = 0 veδ göbek noktasındaki yönü belirler. sabit γ olarak ifade edilebilir
nerede α jeodeziğin sabit çizgilerle yaptığı açı ω. Sınırda b → a, bu azaltılır sinα cosβ = sabit., tanıdık Clairaut ilişkisi. Jacobi'nin sonucunun bir türevi verilmiştir. Darboux (1894), §§583–584); bulduğu çözümü verir Liouville (1846) genel kuadrat yüzeyler için.
Üç eksenli jeodezik araştırması


Üç eksenli bir elipsoid üzerinde, sadece üç basit kapalı jeodezik vardır, elipsoidin üç ana bölümü, X = 0,Y = 0, ve Z = 0.[7]Diğer jeodezikleri araştırmak için, orta ana bölümle kesişen jeodezikleri dikkate almak uygundur, Y = 0, doğru açıda. Bu tür jeodezikler, Şek. Şekil 17 ile aynı elipsoid parametrelerini ve aynı bakış yönünü kullanan 18–22. Ayrıca, bu şekillerin her birinde üç ana elips kırmızı olarak gösterilmiştir.
Başlangıç noktası ise β1 ∈ (−90°, 90°),ω1 = 0, ve α1 = 90°, sonraγ> 0 tegeodezik, elipsoidi "çevresel kutuplar" anlamda çevreler. Jeodezik, ekvatorun kuzey ve güney yönünde dalgalanmaktadır; her bir salınımda, elipsoid etrafındaki tam bir devreden biraz daha azını tamamlar, tipik durumda, jeodezik dolguda iki enlem çizgisi ile sınırlanan alanı doldurur. β = ± β1. Şekil 2'de iki örnek verilmiştir. 18 ve 19. Şekil 18, yassı bir devrim elipsoidiyle pratik olarak aynı davranışı göstermektedir (çünkü a ≈ b); Şekil 9'a kıyasla, ancak, başlangıç noktası daha yüksek bir enlemde ise (Şekil 18), a ≠ b açıktır. Bir dairesel jeodezik için tüm tanjantlar, elipsoid ile kesişen konfokal tek tabakalı hiperboloide temas eder. β = β1(Şaseler 1846 )(Hilbert ve Cohn-Vossen 1952, s. 223–224).


Başlangıç noktası ise β1 = 90°,ω1 ∈ (0°, 180°), veα1 = 180°, sonraγ <0 ve jeodezik, elipsoidini bir "transpolar" duygusunu çevreler. Jeodezik, ellipse'nin doğusunda ve batısında salınır. X = 0; her bir salınımda, elipsoidin etrafındaki tam bir devreden biraz daha fazlasını tamamlar. Tipik durumda, bu, iki boylam çizgisi ile sınırlanan alanı dolduran jeodezik ile sonuçlanır.ω = ω1 ve ω = 180 ° - ω1.Eğer a = btüm meridyenler jeodeziktir; etkisia ≠ b bu tür jeodeziklerin doğu ve batıda salınım yapmasına neden olur. 2 örnek Şek. 20 ve 21. Kutup yakınındaki jeodezik daralması, sınırda kaybolur.b → c; bu durumda, elipsoid aprolat elipsoid haline gelir ve Şekil 20, Şekil 10'a benzer (kendi tarafında döndürülmüş). Bir transpolar jeodeziye tüm teğetler, elipsoid ile kesişen konfokal çift tabakalı hiperboloide temas eder.ω = ω1.

Başlangıç noktası ise β1 = 90°,ω1 = 0° (göbek noktası) veα1 = 135° (jeodezik elipsi terk ederY = 0 dik açılarda), sonraγ = 0 ve jeodezik zıt göbek noktasını tekrar tekrar kesişir ve başlangıç noktasına geri döner. Bununla birlikte, her devrede kesiştiği açıY = 0 yaklaşır 0° veya180° böylece asimptotik olarak jeodezik elips üzerinde Y = 0 (Hart 1849 ) (Arnold 1989, s. 265), Şekil 22'de gösterildiği gibi. Tek bir jeodezik, elipsoid üzerindeki bir alanı doldurmaz. Göbek jeodeziklerine tüm teğetler, elipsoidi theumbilik noktalarda kesen konfokal hiperbola dokunur.
Göbek jeodezik birkaç ilginç özelliğe sahiptir.
- Elipsoidin herhangi bir noktasında iki umbilikal jeodezik vardır.
- Zıt göbek noktaları arasındaki jeodezik mesafe, jeodeziğin başlangıç yönüne bakılmaksızın aynıdır.
- Elipsler üzerinde kapalı jeodezikler ise X = 0 ve Z = 0 stabildir (elipse yakın ve neredeyse paralel bir jeodezik elipse yakın kalır), elips üzerindeki kapalı jeodezik Y = 04 göbek noktasından geçen üssel olarak kararsız. Kaygılıysa, uçaktan dışarı sallanacak Y = 0 ve uçağa yaklaşmadan önce dönüp bak. (Bu davranış, ilk karışıklığın doğasına bağlı olarak tekrar edebilir.)
Başlangıç noktası Bir Bir jeodezik, göbek noktası değildir, zarfı, üzerinde yatan iki sivri uçlu bir astroidtir.β = −β1 ve diğer ikisi açıkω = ω1 + π. İçin kesim yeri Bir çizginin kısmı β = −β1 sivri uçlar arasında.
Başvurular
Doğrudan ve ters jeodezik problemler artık jeodezide bir zamanlar oynadıkları merkezi rolü oynamıyor. Çözmek yerineayarlama nın-nin jeodezik ağlar küresel trigonometride iki boyutlu problem olarak, bu problemler artık üç boyutlu yöntemlerle çözülmektedir (Vincenty ve Bowring 1978 Bununla birlikte, karasal jeodezikler hala birçok alanda önemli bir rol oynamaktadır:
- mesafeleri ve alanları ölçmek için Coğrafi Bilgi Sistemleri;
- Tanımı deniz sınırları (UNCLOS 2006 );
- kurallarında Federal Havacılık İdaresi alan navigasyonu için (RNAV 2007 );
- içindeki mesafeleri ölçme yöntemi FAI Spor Kodu (FAI 2018 ).
- Müslümanların bulmalarına yardım et Mekke'ye doğru yön
Tarafından en az eylem ilkesi Fizikteki birçok problem jeodezik problemlere benzer bir varyasyonel problem olarak formüle edilebilir. Gerçekte, jeodezik problem yüzeyde hareket etmesi kısıtlanmış bir parçacığın hareketine eşdeğerdir, ancak aksi takdirde hiçbir kuvvete maruz kalmaz (Laplace 1799a ) (Hilbert ve Cohn-Vossen 1952, s. Bu nedenle, devrim elipsoidleri veya eksenel elipsoitler gibi basit yüzeylerdeki jeodezikler, yeni yöntemleri keşfetmek için sıklıkla "test durumları" olarak kullanılır. Örnekler şunları içerir:
- eliptik integrallerin gelişimi (Legendre 1811 ) ve eliptik fonksiyonlar (Weierstrass 1861 );
- diferansiyel geometrinin gelişimi (Gauss 1828 ) (Christoffel 1869 );
- bağımsız değişkenlerin değişmesiyle diferansiyel denklem sistemlerini çözme yöntemleri (Jacobi 1839 );
- çalışması kostik (Jacobi 1891 );
- periyodik yörüngelerin sayısı ve kararlılığı ile ilgili araştırmalar (Poincaré 1905 );
- sınırda c → 0, üç eksenli bir elipsoid üzerindeki jeodezikler, dinamik bilardo;
- rastgele sayıda boyuta uzantılar (Knörrer 1980 );
- bir yüzeydeki jeodezik akış (Berger 2010, Çatlak. 12).
Ayrıca bakınız
- Dünya Figürü
- Coğrafi uzaklık
- Büyük daire gezintisi
- Büyük elips
- Jeodezik
- Jeodezi
- Meridyen yayı
- Rhumb hattı
- Vincenty'nin formülleri
Notlar
- ^ Buraya α2 ... ileri azimut BBazı yazarlar hesaplar geri bunun yerine azimut; bu tarafından verilirα2 ± π.
- ^ Laplace (1799a) showed that a particle constrained to move ona surface but otherwise subject to no forces moves along a geodesic forthat surface. Thus, Clairaut's relation is just a consequence ofaçısal momentumun korunumu for a particle on a surface ofrevolution.
- ^ Bagratuni (1962, §17) uses the term "coefficient ofconvergence of ordinates" for the geodesic scale.
- ^ This section is adapted from the documentation for GeographicLib(Karney 2015, Geodesics on a triaxial ellipsoid )
- ^ This notation for the semi-axes is incompatible with that used in theprevious section on ellipsoids of revolution in which a veb stood for the equatorial radius and polar semi-axis.Thus the corresponding inequalities are a = a ≥ b > 0 foran oblate ellipsoid and b ≥ a = a > 0 for a prolateellipsoid.
- ^ The limit b → c gives a prolate ellipsoid withω playing the role of the parametric latitude.
- ^ Eğer c⁄a < 1⁄2, there are other simple closed geodesicssimilar to those shown in Figs. 11 and 12(Klingenberg 1982, §3.5.19).
Referanslar
- Arnold, V.I. (1989). Klasik Mekaniğin Matematiksel Yöntemleri. Translated by Vogtmann, K.; Weinstein, A. (2nd ed.). Springer-Verlag. ISBN 978-0-387-96890-2. OCLC 4037141.CS1 bakimi: ref = harv (bağlantı)
- Bagratuni, G. V. (1967) [1962]. Course in Spheroidal Geodesy. doi:10.5281/zenodo.32371. OCLC 6150611. Translation from Russian of Курс сфероидической геодезии (Moscow, 1962) by U.S. Air Force (FTD-MT-64-390 )
- Berger, M. (2010). Geometry Revealed. Translated by Senechal, L. J. Springer. doi:10.1007/978-3-540-70997-8. ISBN 978-3-540-70996-1.CS1 bakimi: ref = harv (bağlantı)
- Bessel, F.W. (2010) [1825]. Translated by Karney, C. F. F.; Deakin, R. E. "The calculation of longitude and latitude from geodesic measurements". Astronomische Nachrichten. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN .... 331..852K. doi:10.1002 / asna.201011352. İngilizce çevirisi Astron. Nachr. 4, 241–254 (1825). Hatalar.
- Bliss, G.A. (1916). "Jacobi's condition for problems of the calculus of variations in parametric form". Amerikan Matematik Derneği İşlemleri. 17 (2): 195–206. doi:10.1090/S0002-9947-1916-1501037-4 (free access).CS1 bakimi: ref = harv (bağlantı)
- Bomford, G. (1952). Jeodezi. Oxford: Clarendon. OCLC 1396190.CS1 bakimi: ref = harv (bağlantı)
- Borre, K.; Strang, W. G. (2012). Algorithms for Global Positioning. Wellesley-Cambridge Press. ISBN 978-0-9802327-3-8. OCLC 795014501. Bölüm 11, Geometry of the Ellipsoid.CS1 bakimi: ref = harv (bağlantı)
- Cayley, A. (1870). "On the geodesic lines on an oblate spheroid". Felsefi Dergisi. 4. seri. 40 (268): 329–340. doi:10.1080/14786447008640411.CS1 bakimi: ref = harv (bağlantı)
- Chasles, M. (1846). "Sur les lignes géodésiques et les lignes de courbure des surfaces du second degré" [Geodesic lines and the lines of curvature of the surfaces of the second degree] (PDF). Journal de Mathématiques Pures et Appliquées (Fransızcada). 11: 5–20.CS1 bakimi: ref = harv (bağlantı)
- Christoffel, E. B. (1869). "Allgemeine Theorie der geodätischen Dreiecke" [General theory of geodesic triangles]. Abhandlungen Königlichen Akademie der Wissenschaft zu Berlin (in German): 119–176.CS1 bakimi: ref = harv (bağlantı)
- Clairaut, A. C. (1735). "Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini" [Jacques Cassini tarafından çizilen meridyene dik olanın geometrik belirlenmesi]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (Fransızca): 406–416.CS1 bakimi: ref = harv (bağlantı)
- Danielsen, J. S. (1989). "The Area under the Geodesic". Anket İncelemesi. 30 (232): 61–66. doi:10.1179/003962689791474267.CS1 bakimi: ref = harv (bağlantı)
- Darboux, J. G. (1894). Leçons sur la théorie générale des surfaces [Lessons on the general theory of surfaces] (Fransızcada). 3. Paris: Gauthier-Villars. OCLC 8566228. PDF.CS1 bakimi: ref = harv (bağlantı)
- Dupin, P. C. F. (1813). Développements de Géométrie [Developments in geometry] (Fransızcada). Paris: Courcier. OCLC 560800801.CS1 bakimi: ref = harv (bağlantı)
- Ehlert, D. (1993). Methoden der ellipsoidischen Dreiecksberechnung [Methods for ellipsoidal triangulation] (Technical report). Reihe B: Angewandte Geodäsie, Heft Nr. 292 (in German). Deutsche Geodätische Kommission. OCLC 257615376.CS1 bakimi: ref = harv (bağlantı)
- Euler, L. (1755). "Élémens de la trigonométrie sphéroïdique tirés de la méthode des plus grands et plus petits" [Maxima ve minima yönteminden alınan sferoidal trigonometrinin elemanları]. Mémoires de l'Académie Royale des Sciences de Berlin 1753 (Fransızcada). 9: 258–293. Rakamlar.CS1 bakimi: ref = harv (bağlantı)
- FAI (2018). FAI Sporting Code (PDF) (Teknik rapor). Lausanne, Switzerland: Fédération Aéronautique Internationale. Section 8.2.3.CS1 bakimi: ref = harv (bağlantı)
- Forsyth, A. R. (1927). Varyasyon Hesabı. Cambridge Üniv. Basın. ISBN 978-1-107-64083-2. OCLC 250050479.CS1 bakimi: ref = harv (bağlantı)
- Gan'shin, V. V. (1969) [1967]. Geometry of the Earth Ellipsoid. Translated by Willis, J. M. St. Louis: Aeronautical Chart and Information Center. doi:10.5281/zenodo.32854. OCLC 493553. Translation from Russian of Геометрия земного эллипсоида (Moscow, 1967).
- Gauss, C. F. (1902) [1828]. General Investigations of Curved Surfaces of 1827 and 1825. Translated by Morehead, J. C.; Hiltebeitel, A. M. Princeton Univ. Lib. OCLC 7824448. PDF. İngilizce çevirisi Disquisitiones generales circa superficies curvas (Dieterich, Göttingen, 1828).
- Hart, A. S. (1849). "Geometrical demonstration of some properties of geodesic lines". Cambridge ve Dublin Matematik Dergisi. 4: 80–84.CS1 bakimi: ref = harv (bağlantı)
- Helmert, F.R. (1964) [1880]. Mathematical and Physical Theories of Higher Geodesy. 1. St. Louis: Havacılık Harita ve Bilgi Merkezi. doi:10.5281 / zenodo.32050. OCLC 17273288. İngilizce çevirisi Die Mathematischen ve Physikalischen Theorieen der Höheren Geodäsie, Cilt. 1 (Teubner, Leipzig, 1880).
- Hilbert, D.; Cohn-Vossen, S. (1952). Geometri ve Hayal Gücü. Translated by Nemenyi, P. New York: Chelsea. OCLC 301610346.CS1 bakimi: ref = harv (bağlantı)
- Hutton, C. (1811). A Course of Mathematics in Three Volumes Composed for the Use of the Royal Military Academy. Londra: F. C. ve J. Rivington. s.115. OCLC 18031510.CS1 bakimi: ref = harv (bağlantı)
- Jacobi, C. G. J. (1837). "Zur Theorie der Variations-Rechnung und der Differential-Gleichungen" [The theory of the calculus of variations and of differential equations]. Journal für die Reine und Angewandte Mathematik (Almanca'da). 1837 (17): 68–82. doi:10.1515/crll.1837.17.68.CS1 bakimi: ref = harv (bağlantı)
- Jacobi, C. G. J. (1839). "Note von der geodätischen Linie auf einem Ellipsoid und den verschiedenen Anwendungen einer merkwürdigen analytischen Substitution" [The geodesic on an ellipsoid and various applications of a remarkable analytical substitution]. Journal für die Reine und Angewandte Mathematik (Almanca'da). 1839 (19): 309–313. doi:10.1515/crll.1839.19.309. Letter to Bessel, Dec. 28, 1838. Fransızca çeviri (1841).CS1 bakimi: ref = harv (bağlantı)
- Jacobi, C. G. J. (2009) [1866]. A. Clebsch (ed.). Lectures on Dynamics. Translated by Balagangadharan, K. New Delhi: Hindustan Book Agency. ISBN 978-81-85931-91-3. BAY 2569315. OCLC 440645889. İngilizce çevirisi Vorlesungen über Dynamik (Reimer, Berlin, 1866). Hatalar.
- Jacobi, C. G. J. (1891). "Über die Curve, welche alle von einem Punkte ausgehenden geodätischen Linien eines Rotationsellipsoides berührt" [The envelope of geodesic lines emanating from a single point on an ellipsoid]. İçinde K. T. W. Weierstrass (ed.). Jacobi's Gesammelte Werke (Almanca'da). 7. Berlin: Reimer. sayfa 72–87. OCLC 630416023. Op. post., completed by F. H. A. Wangerin. PDF.CS1 bakimi: ref = harv (bağlantı)
- Jekeli, C. (2012), Geometric Reference Systems in Geodesy, Ohio State Univ., hdl:1811/51274CS1 bakimi: ref = harv (bağlantı)
- Jordan, W.; Eggert, O. (1962) [1941]. Jeodezi El Kitabı. 3.2. Translated by Carta, M. W. Washington, DC: Army Map Service. Bibcode:1962hage.book.....J. doi:10.5281/zenodo.35316. OCLC 34429043. İngilizce çevirisi Handbuch der Vermessungskunde, 8th edition (Metzler, Stuttgart, 1941).
- Karney, C. F. F. (2013). "Jeodezikler için algoritmalar". Jeodezi Dergisi. 87 (1): 43–55. arXiv:1109.4448. Bibcode:2013JGeod..87 ... 43K. doi:10.1007 / s00190-012-0578-z (açık Erişim). Addenda.CS1 bakimi: ref = harv (bağlantı)
- Karney, C. F. F. (2015). "GeographicLib". Version 1.44.CS1 bakimi: ref = harv (bağlantı)
- Klingenberg, W. P. A. (1982). Riemannian Geometry. de Gruyer. ISBN 978-3-11-008673-7. BAY 0666697. OCLC 8476832.CS1 bakimi: ref = harv (bağlantı)
- Knörrer, H. (1980). "Geodesics on the ellipsoid". Buluşlar Mathematicae. 59 (2): 119–143. Bibcode:1980InMat..59..119K. doi:10.1007/BF01390041.CS1 bakimi: ref = harv (bağlantı)
- Krakiwsky, E. J.; Thomson, D. B. (1974), Geodetic position computations (PDF), Dept. of Geodesy and Geomatics Engineering, Lecture Notes, Fredericton, N.B.: Univ. of New Brunswick, Bibcode:1974gpc..book.....KCS1 bakimi: ref = harv (bağlantı)
- Laplace, P. S. (1829) [1799a]. Treatise on Celestial Mechanics. 1. Tercüme eden Bowditch, N. Boston: Hillard, Gray, Little, & Wilkins. OCLC 1294937. Book 1, §8.
- Laplace, P. S. (1799b). Traité de Mécanique Céleste [Treatise on Celestial Mechanics] (Fransızcada). 2. Paris: Crapelet. s. 112. OCLC 25448952.CS1 bakimi: ref = harv (bağlantı)
- Legendre, A.M. (1806). "Analyse des triangles tracées sur la surface d'un sphéroïde" [Küresel üçgenlerin analizi]. Mémoires de l'Institut National de France (in French) (1st semester): 130–161.CS1 bakimi: ref = harv (bağlantı)
- Legendre, A.M. (1811). Calcul Intégral sur Divers Alıştırmaları Ordres de Transcendantes ve sur les Quadratures [İntegral Kalkülüste Alıştırmalar] (Fransızcada). Paris: Courcier. OCLC 312469983.CS1 bakimi: ref = harv (bağlantı)
- Leick, A.; Rapoport, L.; Tatarnikov, D. (2015). GPS Satellite Surveying (4. baskı). Wiley. ISBN 978-1-119-01828-5.
- Liouville, J. (1846). "Sur quelques cas particuliers où les équations du mouvement d'un point matériel peuvent s'intégrer" [On special cases where the equations of motion of a point particle can be integrated] (PDF). Journal de Mathématiques Pures et Appliquées (Fransızcada). 11: 345–378.CS1 bakimi: ref = harv (bağlantı)
- Lyusternik, L. (1964). Shortest Paths: Variational Problems. Popular Lectures in Mathematics. 13. Translated by Collins, P.; Brown, R. B. New York: Macmillan. BAY 0178386. OCLC 1048605. Translation from Russian of Кратчайшие Линии: Вариационные Задачи (Moscow, 1955).CS1 bakimi: ref = harv (bağlantı)
- Monge, G. (1850) [1796]. "Sur les lignes de courbure de la surface de l'ellipsoïde" [On the lines of curvature on the surface of the ellipsoid]. İçinde J. Liouville (ed.). Application de l'Analyse à la Géometrie (Fransızca) (5. baskı). Paris: Bachelier. s. 139–160. OCLC 2829112. Rakamlar.
- Ulusal Jeodezik Araştırma (2012). "Geodesic Utilities: Inverse and Forward". Version 3.0.
- Newton, I. (1848) [1687]. The Mathematical Principles of Natural Philosophy. Translated by Motte, A. New York: Adee. s.405. Book 3, Proposition 19, Problem 3, pp. 405–409.
- Oriani, B. (1806). "Elementi di trigonometria sferoidica, Pt. 1" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (italyanca). 1 (1): 118–198.CS1 bakimi: ref = harv (bağlantı)
- Oriani, B. (1808). "Elementi di trigonometria sferoidica, Pt. 2" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (italyanca). 2 (1): 1–58.CS1 bakimi: ref = harv (bağlantı)
- Oriani, B. (1810). "Elementi di trigonometria sferoidica, Pt. 3" [Elements of spheroidal trigonometry]. Memorie Dell'Istituto Nazionale Italiano (italyanca). 2 (2): 1–58.CS1 bakimi: ref = harv (bağlantı)
- Poincaré, H. (1905). "Sur les lignes géodésiques des surfaces convexes" [Geodesics lines on convex surfaces]. Amerikan Matematik Derneği İşlemleri (Fransızcada). 6 (3): 237–274. doi:10.2307/1986219. JSTOR 1986219.CS1 bakimi: ref = harv (bağlantı)
- Rainsford, H. F. (1955). "Long geodesics on the ellipsoid". Bülten Géodésique. 37 (1): 12–22. Bibcode:1955BGeod..29...12R. doi:10.1007/BF02527187.CS1 bakimi: ref = harv (bağlantı)
- Rapp, R. H. (1991), Geometric geodesy, part I, Ohio State Univ., hdl:1811/24333CS1 bakimi: ref = harv (bağlantı)
- Rapp, R. H. (1993), Geometric geodesy, part II, Ohio State Univ., hdl:1811/24409CS1 bakimi: ref = harv (bağlantı)
- RNAV (2007). Order 8260.54A, The United States Standard for Area Navigation (PDF) (Teknik rapor). Washington, D.C.: U.S. Federal Aviation Administration. Ek 2.CS1 bakimi: ref = harv (bağlantı)
- Sjöberg, L. E. (2006). "Determination of areas on the plane, sphere and ellipsoid". Anket İncelemesi. 38 (301): 583–593. doi:10.1179/003962606780732100.CS1 bakimi: ref = harv (bağlantı)
- UNCLOS (2006). A Manual on Technical Aspects of the United Nations Convention on the Law of the Sea, 1982 (PDF) (Teknik rapor) (4. baskı). Monaco: International Hydrographic Bureau.CS1 bakimi: ref = harv (bağlantı)
- Vincenty, T. (1975). "Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations" (PDF). Anket İncelemesi. 23 (176): 88–93. doi:10.1179 / sre.1975.23.176.88. Ek: Anket İncelemesi 23 (180): 294 (1976).CS1 bakimi: ref = harv (bağlantı)
- Vincenty, T.; Bowring, B. R. (1978). Application of three-dimensional geodesy to adjustments of horizontal networks (PDF) (Teknik rapor). NOAA. NOS NGS-13.CS1 bakimi: ref = harv (bağlantı)
- Weierstrass, K. T. W. (1861). "Über die geodätischen Linien auf dem dreiaxigen Ellipsoid" [Geodesic lines on a triaxial ellipsoid]. Monatsberichte der Königlichen Akademie der Wissenschaft zu Berlin (in German): 986–997. PDF.CS1 bakimi: ref = harv (bağlantı)
Dış bağlantılar
- Online geodesic bibliography of books and articles on geodesics on ellipsoids.
- Test set for geodesics, a set of 500000 geodesics for the WGS84 ellipsoid, computed using high-precision arithmetic.
- NGS tool uygulama Vincenty (1975).
- geod(1), man page for the PROJE utility for geodesic calculations.
- GeographicLib implementation nın-nin Karney (2013).
- Drawing geodesics on Google Maps.


































![{ displaystyle { begin {align} delta & = int { frac {{ sqrt {b ^ {2} sin ^ {2} beta + c ^ {2} cos ^ {2} beta }} , d beta} {{ sqrt {a ^ {2} -b ^ {2} sin ^ {2} beta -c ^ {2} cos ^ {2} beta}} { sqrt {{ bigl (} b ^ {2} -c ^ {2} { bigr)} cos ^ {2} beta - gamma}}}} [6pt] & quad - int { frac {{ sqrt {a ^ {2} sin ^ {2} omega + b ^ {2} cos ^ {2} omega}} , d omega} {{ sqrt {a ^ { 2} sin ^ {2} omega + b ^ {2} cos ^ {2} omega -c ^ {2}}} { sqrt {{ bigl (} a ^ {2} -b ^ { 2} { bigr)} sin ^ {2} omega + gamma}}}}. End {hizalı}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b5c88b1ff894b8ebb8772e0a41e8a6d2c37094)
