Homomorfizm - Homomorphism - Wikipedia

İçinde cebir, bir homomorfizm bir yapıyı koruyan harita ikisi arasında cebirsel yapılar aynı türden (örneğin iki grupları, iki yüzükler, ya da iki vektör uzayları ). Kelime homomorfizm dan geliyor antik Yunan dili: ὁμός (homolar) "aynı" anlamına gelir ve μορφή (morphe) "biçim" veya "şekil" anlamına gelir. Bununla birlikte, kelime matematiğe Almanca'nın (yanlış) bir tercümesi nedeniyle tanıtıldı. ähnlich anlamına "benzer" ὁμός "aynı" anlamına gelir.^[1] "Homomorfizm" terimi, Alman matematikçiye atfedildiği 1892 gibi erken bir tarihte ortaya çıktı. Felix Klein (1849–1925).^[2]

Vektör uzaylarının homomorfizmleri de denir doğrusal haritalar ve çalışmaları şunun amacıdır: lineer Cebir.

Homomorfizm kavramı, adı altında genelleştirilmiştir. morfizm, altta yatan bir kümesi olmayan veya cebirsel olmayan diğer birçok yapıya. Bu genelleme başlangıç noktasıdır kategori teorisi.

Bir homomorfizm aynı zamanda bir izomorfizm, bir endomorfizm, bir otomorfizm vb. (aşağıya bakın). Bunların her biri, herhangi bir morfizm sınıfına genelleştirilebilecek bir şekilde tanımlanabilir.

Tanım

Bir homomorfizm, ikisi arasındaki bir haritadır cebirsel yapılar aynı türden (aynı adı taşıyan), operasyonlar yapıların. Bu bir harita ${ displaystyle f: A - B}$ ikisi arasında setleri ${ displaystyle A}$ , ${ displaystyle B}$ aynı yapıya sahip olacak şekilde ${ displaystyle cdot}$ yapının bir işlemidir (burada basitleştirme amacıyla, bir ikili işlem ), sonra

{ displaystyle f (x cdot y) = f (x) cdot f (y)}

her çift için ${ displaystyle x}$ , ${ displaystyle y}$ öğelerinin ${ displaystyle A}$ .^{[not 1]} Biri sık sık şunu söylüyor ${ displaystyle f}$ işlemi korur veya işlemle uyumludur.

Resmen, bir harita ${ displaystyle f: A - B}$ bir operasyonu korur ${ displaystyle mu}$ nın-nin derece k, her ikisinde de tanımlanmış ${ displaystyle A}$ ve ${ displaystyle B}$ Eğer

{ displaystyle f ( mu _ {A} (a_ {1}, ldots, a_ {k})) = mu _ {B} (f (a_ {1}), ldots, f (a_ {k })),}

tüm unsurlar için ${ displaystyle a_ {1}, ..., a_ {k}}$ içinde ${ displaystyle A}$ .

Bir homomorfizm tarafından korunması gereken işlemler şunları içerir: 0-ary işlemler sabitler budur. Özellikle, bir kimlik öğesi yapının tipine göre gerekliyse, birinci yapının kimlik öğesi, ikinci yapının karşılık gelen kimlik öğesi ile eşleştirilmelidir.

Örneğin:

Bir yarıgrup homomorfizmi arasında bir harita yarı gruplar yarı grup işlemini koruyan.
Bir monoid homomorfizm arasında bir harita monoidler Monoid işlemi koruyan ve birinci monoidin kimlik öğesini ikinci monoidinkiyle eşleyen (kimlik öğesi bir 0-ary operasyon ).
Bir grup homomorfizmi arasında bir harita grupları grup çalışmasını koruyan. Bu, grup homomorfizminin, birinci grubun kimlik öğesini ikinci grubun kimlik öğesi ile eşleştirdiğini ve ters birinci grubun bir elemanının bu elemanın görüntüsünün tersine. Bu nedenle, gruplar arasında bir yarı grup homomorfizmi, zorunlu olarak bir grup homomorfizmidir.
Bir halka homomorfizmi arasında bir harita yüzükler halka toplamayı, halka çarpımını ve çarpımsal kimlik. Çarpımsal kimliğin korunup korunmayacağı tanımına bağlıdır. yüzük kullanımda. Çarpımsal kimlik korunmazsa, birinin bir rng homomorfizm.
Bir doğrusal harita homomorfizmdir vektör alanı, Bu, değişmeli grup yapısını koruyan vektör uzayları arasındaki grup homomorfizmidir ve skaler çarpım.
Bir modül homomorfizmi arasında doğrusal bir harita olarak da adlandırılır modüller benzer şekilde tanımlanır.
Bir cebir homomorfizmi koruyan bir haritadır cebir operasyonlar.

Cebirsel bir yapının birden fazla operasyonu olabilir ve her operasyonu korumak için bir homomorfizm gerekir. Dolayısıyla, sadece bazı operasyonları koruyan bir harita, yapının bir homomorfizmi değil, sadece korunan operasyonlar dikkate alınarak elde edilen alt yapının bir homomorfizmidir. Örneğin, özdeşlik öğesini değil, monoid işlemi koruyan monoidler arasındaki bir harita, monoid bir homomorfizm değil, yalnızca bir yarıgrup homomorfizmidir.

Bir homomorfizmin kaynağında ve hedefinde işlemlerin gösterimi aynı olmak zorunda değildir. Örneğin, gerçek sayılar toplama için bir grup oluşturur ve pozitif gerçek sayılar çarpma için bir grup oluşturur. üstel fonksiyon

{ displaystyle x mapsto e ^ {x}}

tatmin eder

{ displaystyle e ^ {x + y} = e ^ {x} e ^ {y},}

ve bu nedenle bu iki grup arasında bir homomorfizmdir. Hatta bir izomorfizmdir (aşağıya bakınız), çünkü ters fonksiyon, doğal logaritma, tatmin eder

{ displaystyle ln (xy) = ln (x) + ln (y),}

ve aynı zamanda bir grup homomorfizmidir.

Örnekler

Monoid homomorfizm

{ displaystyle f}

monoidden

(N, +, 0)

monoide

(N, \times, 1)

, tarafından tanımlanan

{ displaystyle f (x) = 2 ^ {x}}

. Bu enjekte edici, Ama değil örten.

gerçek sayılar bir yüzük, hem toplama hem de çarpmaya sahip. Tüm 2 × 2 seti matrisler aynı zamanda bir yüzük matris toplama ve matris çarpımı. Bu halkalar arasında bir işlevi şu şekilde tanımlarsak:

{ displaystyle f (r) = { başlar {pmatrix} r & 0 0 ve r end {pmatrix}}}

nerede $r$ gerçek bir sayıdır $f$ halkaların homomorfizmidir, çünkü $f$ her iki eklemeyi de korur:

{ displaystyle f (r + s) = { başlar {pmatrix} r + s & 0 0 & r + s end {pmatrix}} = { begin {pmatrix} r & 0 0 & r end {pmatrix}} + { başlangıç ​​{pmatrix} s & 0 0 & s end {pmatrix}} = f (r) + f (s)}

ve çarpma:

{ displaystyle f (rs) = { begin {pmatrix} rs & 0 0 & rs end {pmatrix}} = { begin {pmatrix} r & 0 0 & r end {pmatrix}} { begin {pmatrix} s & 0 0 & s end {pmatrix}} = f (r) , f (s).}

Başka bir örnek için, sıfır olmayan Karışık sayılar oluşturmak grup Çarpma işlemi altında, sıfır olmayan gerçek sayılar gibi. (Sıfır, her iki gruptan da çıkarılmalıdır çünkü bir çarpımsal ters, bir grubun öğeleri için gereklidir.) Bir işlev tanımlayın ${ displaystyle f}$ sıfır olmayan karmaşık sayılardan sıfır olmayan gerçek sayılara

{ displaystyle f (z) = | z |.}

Yani, ${ displaystyle f}$ ... mutlak değer karmaşık sayının (veya modülü) ${ displaystyle z}$ . Sonra ${ displaystyle f}$ çarpımı koruduğu için grupların homomorfizmidir:

{ displaystyle f (z_ {1} z_ {2}) = | z_ {1} z_ {2} | = | z_ {1} || z_ {2} | = f (z_ {1}) f (z_ { 2}).}

Bunu not et $f$ toplamayı korumadığı için halkaların homomorfizmine (karmaşık sayılardan gerçek sayılara) genişletilemez:

{ displaystyle | z_ {1} + z_ {2} | neq | z_ {1} | + | z_ {2} |.}

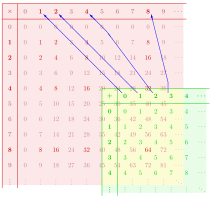
Başka bir örnek olarak, diyagram bir monoid homomorfizm ${ displaystyle f}$ monoidden ${ displaystyle ( mathbb {N}, +, 0)}$ monoide ${ displaystyle ( mathbb {N}, times, 1)}$ . Karşılık gelen işlemlerin farklı isimleri nedeniyle, yapı koruma özellikleri, ${ displaystyle f}$ miktar ${ displaystyle f (x + y) = f (x) çarpı f (y)}$ ve ${ displaystyle f (0) = 1}$ .

Bir kompozisyon cebiri ${ displaystyle A}$ bir tarla üzerinde ${ displaystyle F}$ var ikinci dereceden form, deniliyor norm, ${ displaystyle N: A ila F}$ bir grup homomorfizmi olan çarpımsal grup nın-nin ${ displaystyle A}$ çarpımsal grubuna ${ displaystyle F}$ .

Özel homomorfizmler

Birkaç tür homomorfizm, genel olarak da tanımlanan belirli bir ada sahiptir. morfizmler.

İzomorfizm

Bir izomorfizm arasında cebirsel yapılar aynı türden genel olarak şöyle tanımlanır: önyargılı homomorfizm.^[3]^:134 ^[4]^:28

Daha genel bağlamda kategori teorisi bir izomorfizm, bir morfizm olan ters bu aynı zamanda bir morfizmdir. Cebirsel yapıların özel durumunda, iki tanım eşdeğerdir, ancak altta yatan bir kümeye sahip olan cebirsel olmayan yapılar için farklılık gösterebilir.

Daha doğrusu, eğer

{ displaystyle f: A - B}

bir (homo) morfizmdir, bir homomorfizm varsa tersi vardır

{ displaystyle g: B - A}

öyle ki

{ displaystyle f circ g = operatorname {Id} _ {B} qquad { text {ve}} qquad g circ f = operatorname {Id} _ {A}.}

Eğer ${ displaystyle A}$ ve ${ displaystyle B}$ temel kümeler var ve ${ displaystyle f: A - B}$ tersi var ${ displaystyle g}$ , sonra ${ displaystyle f}$ önyargılıdır. Aslında, ${ displaystyle f}$ dır-dir enjekte edici, gibi ${ displaystyle f (x) = f (y)}$ ima eder ${ displaystyle x = g (f (x)) = g (f (y)) = y}$ , ve ${ displaystyle f}$ dır-dir örten herhangi biri için ${ displaystyle x}$ içinde ${ displaystyle B}$ , birinde var ${ displaystyle x = f (g (x))}$ , ve ${ displaystyle x}$ bir öğesinin görüntüsüdür ${ displaystyle A}$ .

Tersine, eğer ${ displaystyle f: A - B}$ cebirsel yapılar arasında bijektif homomorfizmdir. ${ displaystyle g: B - A}$ harita ol öyle ki ${ displaystyle g (y)}$ eşsiz unsurdur ${ displaystyle x}$ nın-nin ${ displaystyle A}$ öyle ki ${ displaystyle f (x) = y}$ . Birinde var ${ displaystyle f circ g = operatorname {Id} _ {B} { text {ve}} g circ f = operatorname {Id} _ {A},}$ ve sadece bunu göstermek için kalır $g$ bir homomorfizmdir. Eğer ${ displaystyle *}$ her çift için yapının ikili işlemidir ${ displaystyle x}$ , ${ displaystyle y}$ öğelerinin ${ displaystyle B}$ , birinde var

{ displaystyle g (x * _ {B} y) = g (f (g (x)) * _ {B} f (g (y))) = g (f (g (x) * _ {A} g (y))) = g (x) * _ {A} g (y),}

ve ${ displaystyle g}$ bu nedenle uyumludur ${ displaystyle *.}$ Kanıt herhangi biri için benzer olduğu için derece bu gösteriyor ki ${ displaystyle g}$ bir homomorfizmdir.

Bu ispat cebirsel olmayan yapılar için geçerli değildir. Örnekler için topolojik uzaylar, bir morfizm bir sürekli harita ve bir önyargılı sürekli haritanın tersi mutlaka sürekli değildir. Topolojik uzayların bir izomorfizmi homomorfizm veya iki sürekli harita bu nedenle tersi de sürekli olan, yanlı bir sürekli haritadır.

Endomorfizm

Bir endomorfizm bir homomorfizmdir alan adı eşittir ortak alan veya daha genel olarak a morfizm kaynağı hedefe eşittir.^[3]^:135

Bir cebirsel yapının veya bir nesnenin endomorfizmleri kategori oluşturmak monoid kompozisyon altında.

A'nın endomorfizmleri vektör alanı veya bir modül oluşturmak yüzük. Bir vektör uzayı veya bir ücretsiz modül sonlu boyut, seçimi temel bir halka izomorfizmi endomorfizm halkası ve halkası arasında kare matrisler aynı boyutta.

Otomorfizm

Bir otomorfizm aynı zamanda bir izomorfizm olan bir endomorfizmdir.^[3]^:135

Bir cebirsel yapının veya bir kategorideki bir nesnenin otomorfizmleri bir grup denilen kompozisyon altında otomorfizm grubu yapının.

Bir isim alan birçok grup, bazı cebirsel yapıların otomorfizm gruplarıdır. Örneğin, genel doğrusal grup ${ displaystyle operatöradı {GL} _ {n} (k)}$ bir otomorfizm grubudur vektör alanı boyut ${ displaystyle n}$ üzerinde alan ${ displaystyle k}$ .

Otomorfizm grupları alanlar tarafından tanıtıldı Évariste Galois çalışmak için kökler nın-nin polinomlar ve temeli Galois teorisi.

Monomorfizm

Cebirsel yapılar için, monomorfizmler genellikle şu şekilde tanımlanır: enjekte edici homomorfizmler.^[3]^:134 ^[4]^:29

Daha genel bağlamda kategori teorisi bir monomorfizm, bir morfizm yani iptal edilebilir bırakıldı.^[5] Bu, bir (homo) morfizmin ${ displaystyle f: A - B}$ herhangi bir çift için bir monomorfizmdir ${ displaystyle g}$ , ${ displaystyle h}$ başka herhangi bir nesneden morfizm ${ displaystyle C}$ -e ${ displaystyle A}$ , sonra ${ displaystyle f circ g = f circ h}$ ima eder ${ displaystyle g = h}$ .

Bu iki tanım monomorfizm tüm yaygın cebirsel yapılar için eşdeğerdir. Daha doğrusu, eşdeğerdirler alanlar, her homomorfizmin bir monomorfizm olduğu ve çeşitleri nın-nin evrensel cebir, yani işlemler ve aksiyomların (özdeşlikler) herhangi bir kısıtlama olmaksızın tanımlandığı cebirsel yapılardır (alanlar çeşit değildir, çünkü çarpımsal ters ya bir tekli işlem veya çarpma işleminin bir özelliği olarak, her iki durumda da yalnızca sıfır olmayan öğeler için tanımlanmıştır).

Özellikle, bir monomorfizmin iki tanımı aşağıdakiler için eşdeğerdir: setleri, magmalar, yarı gruplar, monoidler, grupları, yüzükler, alanlar, vektör uzayları ve modüller.

Bir bölünmüş monomorfizm bir homomorfizmdir sol ters ve bu nedenle kendisi diğer homomorfizmin tam tersidir. Yani bir homomorfizm ${ displaystyle f iki nokta üst üste A ila B}$ bir homomorfizm varsa bölünmüş bir homomorfizmdir ${ displaystyle g iki nokta üst üste B ila A}$ öyle ki ${ displaystyle g circ f = operatorname {Id} _ {A}.}$ Bölünmüş bir monomorfizm, her iki anlam için de her zaman bir monomorfizmdir. monomorfizm. Kümeler ve vektör uzayları için, her monomorfizm bölünmüş bir homomorfizmdir, ancak bu özellik çoğu yaygın cebirsel yapılar için geçerli değildir.

İki monomorfizm tanımının denkliğinin kanıtı

Enjekte edici bir homomorfizm iptal edilebilir olarak bırakılır: Eğer ${ displaystyle f circ g = f circ h,}$ birinde var ${ displaystyle f (g (x)) = f (h (x))}$ her biri için ${ displaystyle x}$ içinde ${ displaystyle C}$ ortak kaynağı ${ displaystyle g}$ ve ${ displaystyle h}$ . Eğer ${ displaystyle f}$ enjekte edici, o zaman ${ displaystyle g (x) = h (x)}$ , ve böylece ${ displaystyle g = h}$ . Bu kanıt yalnızca cebirsel yapılar için değil, aynı zamanda herhangi bir kategori nesneleri kümeler ve oklar bu kümeler arasındaki eşlemlerdir. Örneğin, sürekli bir enjeksiyon haritası, kategorisindeki bir monomorfizmdir. topolojik uzaylar.

Tersine, sol iptal edilebilir bir homomorfizmin enjekte edici olduğunu kanıtlamak için, özgür nesne açık ${ displaystyle x}$ . Verilen bir Çeşitlilik cebirsel yapıların üzerinde özgür bir nesne ${ displaystyle x}$ cebirsel bir yapıdan oluşan bir çifttir ${ displaystyle L}$ bu çeşitlilik ve bir unsur ${ displaystyle x}$ nın-nin ${ displaystyle L}$ aşağıdakileri tatmin etmek evrensel mülkiyet: her yapı için ${ displaystyle S}$ çeşitlilik ve her unsur ${ displaystyle s}$ nın-nin ${ displaystyle S}$ benzersiz bir homomorfizm var ${ displaystyle f: L - S}$ öyle ki ${ displaystyle f (x) = s}$ . Örneğin, setler için serbest nesne ${ displaystyle x}$ basitçe ${ displaystyle {x }}$ ; için yarı gruplar, özgür nesne ${ displaystyle x}$ dır-dir ${ displaystyle {x, x ^ {2}, ldots, x ^ {n}, ldots },}$ ki, bir yarı grup olarak, pozitif tamsayıların toplamsal yarı grubuna izomorfiktir; için monoidler, özgür nesne ${ displaystyle x}$ dır-dir ${ displaystyle {1, x, x ^ {2}, ldots, x ^ {n}, ldots },}$ bu, bir monoid olarak, negatif olmayan tam sayıların toplamsal monoidine izomorfiktir; için grupları, özgür nesne ${ displaystyle x}$ ... sonsuz döngüsel grup ${ displaystyle { ldots, x ^ {- n}, ldots, x ^ {- 1}, 1, x, x ^ {2}, ldots, x ^ {n}, ldots },}$ bu, bir grup olarak, tamsayıların toplamsal grubuna izomorfiktir; için yüzükler, özgür nesne ${ displaystyle x}$ } polinom halkası ${ displaystyle mathbb {Z} [x];}$ için vektör uzayları veya modüller, özgür nesne ${ displaystyle x}$ vektör uzayı veya sahip olan serbest modüldür ${ displaystyle x}$ temel olarak.

Özgür bir nesne bittiğinde ${ displaystyle x}$ var, sonra her sol iptal edilebilir homomorfizm enjekte ediyor: İzin Vermek ${ displaystyle f iki nokta üst üste A ila B}$ sol iptal edilebilir bir homomorfizm olmak ve ${ displaystyle a}$ ve ${ displaystyle b}$ iki unsuru olmak ${ displaystyle A}$ böyle ${ displaystyle f (a) = f (b)}$ . Serbest nesnenin tanımına göre ${ displaystyle F}$ homomorfizmler var ${ displaystyle g}$ ve ${ displaystyle h}$ itibaren ${ displaystyle F}$ -e ${ displaystyle A}$ öyle ki ${ displaystyle g (x) = a}$ ve ${ displaystyle h (x) = b}$ . Gibi ${ displaystyle f (g (x)) = f (h (x))}$ , birinde var ${ displaystyle f circ g = f circ h,}$ evrensel bir özelliğin tanımındaki benzersizlikle. Gibi ${ displaystyle f}$ iptal edilebilir bırakılırsa ${ displaystyle g = h}$ , ve böylece ${ displaystyle a = b}$ . Bu nedenle, ${ displaystyle f}$ enjekte edici.

Üzerinde ücretsiz bir nesnenin varlığı ${ displaystyle x}$ için Çeşitlilik (Ayrıca bakınız Özgür nesne § Varlık ): Üzerinde özgür bir nesne oluşturmak için ${ displaystyle x}$ seti düşünün ${ displaystyle W}$ of iyi biçimlendirilmiş formüller ... dan inşa edildi ${ displaystyle x}$ ve yapının işlemleri. Aksiyomları uygulayarak biri birinden diğerine geçebilirse, bu tür iki formülün eşdeğer olduğu söylenir (kimlikler yapının). Bu bir denklik ilişkisi kimlikler koşullara tabi değilse, yani çeşitlilikle çalışıyorsa. Daha sonra çeşitliliğin işlemleri sette iyi tanımlanmıştır. denklik sınıfları nın-nin ${ displaystyle W}$ bu ilişki için. Ortaya çıkan nesnenin ücretsiz bir nesne olduğunu göstermek basittir. ${ displaystyle W}$ .

Epimorfizm

İçinde cebir, epimorfizmler genellikle şu şekilde tanımlanır: örten homomorfizmler.^[3]^:134^[4]^:43 Öte yandan, kategori teorisi, epimorfizmler olarak tanımlanır doğru iptal edilebilir morfizmler.^[5] Bu, bir (homo) morfizmin ${ displaystyle f: A - B}$ herhangi bir çift için bir epimorfizmdir ${ displaystyle g}$ , ${ displaystyle h}$ morfizmlerin ${ displaystyle B}$ başka herhangi bir nesneye ${ displaystyle C}$ eşitlik ${ displaystyle g circ f = h circ f}$ ima eder ${ displaystyle g = h}$ .

Suretsel bir homomorfizm her zaman doğru iptal edilebilir, ancak tersi cebirsel yapılar için her zaman doğru değildir. Ancak, iki tanım epimorfizm eşdeğerdir setleri, vektör uzayları, değişmeli gruplar, modüller (kanıt için aşağıya bakın) ve grupları.^[6] Bu yapıların tüm matematikte ve özellikle de lineer Cebir ve homolojik cebir, iki eşdeğer olmayan tanımın bir arada varlığını açıklayabilir.

Örtücü olmayan epimorfizmlerin bulunduğu cebirsel yapılar şunları içerir: yarı gruplar ve yüzükler. En temel örnek, aşağıdakilerin dahil edilmesidir: tamsayılar içine rasyonel sayılar, halkaların ve çarpımsal yarı grupların bir homomorfizmi. Her iki yapı için de bir monomorfizm ve örten olmayan bir epimorfizmdir, ancak bir izomorfizm değildir.^[5]^[7]

Bu örneğin geniş bir genellemesi, bir yüzüğün lokalizasyonu çarpımsal bir küme ile. Her yerelleştirme bir halka epimorfizmidir ve genel olarak örten değildir. Yerelleştirmeler temel olduğundan değişmeli cebir ve cebirsel geometri Bu, neden bu alanlarda epimorfizmlerin doğru iptal edilebilir homomorfizmler olarak tanımlanmasının genellikle tercih edildiğini açıklayabilir.

Bir bölünmüş epimorfizm bir homomorfizmdir sağ ters ve bu yüzden kendisi diğer homomorfizmin sol tersidir. Yani bir homomorfizm ${ displaystyle f iki nokta üst üste A ila B}$ bir homomorfizm varsa bölünmüş bir epimorfizmdir ${ displaystyle g iki nokta üst üste B ila A}$ öyle ki ${ displaystyle f circ g = operatorname {Id} _ {B}.}$ Bölünmüş bir epimorfizm, her iki anlam için de her zaman bir epimorfizmdir. epimorfizm. Kümeler ve vektör uzayları için, her epimorfizm bölünmüş bir epimorfizmdir, ancak bu özellik en yaygın cebirsel yapılar için geçerli değildir.

Özetle, biri var

{ displaystyle { text {split epimorphism}} { text {epimorphism (surjective)}} anlamına gelir { text {epimorphism (sağ iptal edilebilir)}};}

son çıkarım, kümeler, vektör uzayları, modüller ve değişmeli gruplar için bir eşdeğerliktir; ilk çıkarım, kümeler ve vektör uzayları için bir eşdeğerliktir.

Epimorfizmin iki tanımının denkliği

İzin Vermek ${ displaystyle f iki nokta üst üste A ila B}$ bir homomorfizm ol. Süpervatif değilse, iptal edilemez olduğunu kanıtlamak istiyoruz.

Setler söz konusu olduğunda ${ displaystyle b}$ unsuru olmak ${ displaystyle B}$ ait olmayan ${ displaystyle f (A)}$ ve tanımla ${ displaystyle g, h kolon B - B}$ öyle ki ${ displaystyle g}$ ... kimlik işlevi, ve şu ${ displaystyle h (x) = x}$ her biri için ${ displaystyle x B'de}$ bunun haricinde ${ displaystyle h (b)}$ başka herhangi bir unsurdur ${ displaystyle B}$ . Açıkça ${ displaystyle f}$ haklı olarak iptal edilemez ${ displaystyle g neq h}$ ve ${ displaystyle g circ f = h circ f.}$

Vektör uzayları, değişmeli gruplar ve modüller söz konusu olduğunda, ispat şunun varlığına dayanır: kokerneller ve gerçeği üzerine sıfır harita homomorfizmlerdir: let ${ displaystyle C}$ çekirdeği olmak ${ displaystyle f}$ , ve ${ displaystyle g iki nokta üst üste B ila C}$ kanonik harita olabilir, öyle ki ${ displaystyle g (f (A)) = 0}$ . İzin Vermek ${ displaystyle h kolon B ila C}$ sıfır haritası olun. Eğer ${ displaystyle f}$ örten değil ${ displaystyle C neq 0}$ , ve böylece ${ displaystyle g neq h}$ (biri sıfır haritasıdır, diğeri değildir). Böylece ${ displaystyle f}$ iptal edilemez, çünkü ${ displaystyle g circ f = h circ f}$ (her ikisi de sıfır haritasıdır ${ displaystyle A}$ -e ${ displaystyle C}$ ).

Çekirdek

Herhangi bir homomorfizm ${ displaystyle f: X - Y}$ tanımlar denklik ilişkisi ${ displaystyle sim}$ açık ${ displaystyle X}$ tarafından ${ displaystyle a sim b}$ ancak ve ancak ${ displaystyle f (a) = f (b)}$ . İlişki ${ displaystyle sim}$ denir çekirdek nın-nin ${ displaystyle f}$ . Bu bir uyum ilişkisi açık ${ displaystyle X}$ . bölüm kümesi ${ displaystyle X / { sim}}$ daha sonra aynı tipte bir yapı verilebilir ${ displaystyle X}$ doğal bir şekilde, bölümün işlemlerini tanımlayarak ${ displaystyle [x] ast [y] = [x ast y]}$ her işlem için ${ displaystyle ast}$ nın-nin ${ displaystyle X}$ . Bu durumda ${ displaystyle X}$ içinde ${ displaystyle Y}$ homomorfizm altında ${ displaystyle f}$ zorunlu olarak izomorf -e ${ displaystyle X / ! sim}$ ; bu gerçek şunlardan biridir izomorfizm teoremleri.

Cebirsel yapı bir grup bazı işlemler için denklik sınıfı ${ displaystyle K}$ of kimlik öğesi Bu işlemin, denklik ilişkisini karakterize etmek için yeterlidir. Bu durumda, eşdeğerlik bağıntısına göre bölüm, ${ displaystyle X / K}$ (genellikle " ${ displaystyle X}$ mod ${ displaystyle K}$ "). Ayrıca bu durumda, ${ displaystyle K}$ , ziyade ${ displaystyle sim}$ buna denir çekirdek nın-nin ${ displaystyle f}$ . Belirli bir cebirsel yapının homomorfizmlerinin çekirdekleri doğal olarak bazı yapılarla donatılmıştır. Çekirdeklerin bu yapı türü, söz konusu yapı ile aynıdır. değişmeli gruplar, vektör uzayları ve modüller, ancak farklıdır ve diğer durumlarda belirli bir ad almıştır, örneğin normal alt grup çekirdekleri için grup homomorfizmleri ve idealler çekirdekleri için halka homomorfizmleri (değişmeli olmayan halkalar durumunda, çekirdekler iki taraflı idealler ).

İlişkisel yapılar

İçinde model teorisi cebirsel yapı kavramı, hem işlemleri hem de ilişkileri içeren yapılara genelleştirilmiştir. İzin Vermek L işlev ve ilişki sembollerinden oluşan bir imza olmalı ve Bir, B iki olmak Lyapılar. Sonra bir homomorfizm itibaren Bir -e B bir haritalama h etki alanından Bir alanına B öyle ki

h(F^Bir(a₁,…,a_n)) = F^B(h(a₁),…,h(a_n)) her biri için n-ary işlev sembolü F içinde L,
R^Bir(a₁,…,a_n) ima eder R^B(h(a₁),…,h(a_n)) her biri için n-ary ilişki sembolü R içinde L.

Sadece bir ikili ilişkinin olduğu özel durumda, a kavramını elde ederiz. grafik homomorfizmi. İlişkisel homomorfizmler ve izomorfizmler hakkında ayrıntılı bir tartışma için bkz.^[8]

Biçimsel dil teorisi

Homomorfizmler ayrıca resmi diller^[9] ve genellikle kısaca morfizmler olarak anılır.^[10] Verilen alfabeler Σ₁ ve Σ₂, bir işlev h : Σ₁^∗ → Σ₂^∗ öyle ki h(uv) = h(sen) h(v) hepsi için sen ve v Σ içinde₁^∗ denir homomorfizm üzerinde Σ₁^∗.^{[not 2]} Eğer h Σ üzerinde bir homomorfizmdir₁^∗ ve e boş kelimeyi gösterir, sonra h denir e-içermeyen homomorfizm ne zaman h(x) ≠ e hepsi için x ≠ e Σ içinde₁^∗.

Set Σ^∗ Alfabeden oluşan kelimelerin Σ'si olarak düşünülebilir serbest monoid tarafından oluşturulmuştur. Burada monoid işlem bitiştirmedir ve kimlik öğesi boş kelimedir. Bu perspektiften bakıldığında, bir dil homormorfizmi tam olarak monoid bir homomorfizmdir.^{[not 3]}

Ayrıca bakınız

Sürekli işlev
Diffeomorfizm
Homomorfik şifreleme
Homomorfik gizli paylaşım - basit bir merkezi olmayan oylama protokolü
Morfizm

Notlar

^ Her zaman olmamakla birlikte çoğu zaman olduğu gibi, her ikisinin de çalışması için aynı sembol ${ displaystyle A}$ ve ${ displaystyle B}$ burada kullanıldı.
^ ∗, Kleene yıldızı operasyon, Σ^∗ Boş kelime dahil olmak üzere Σ alfabesinden oluşan kelime grubunu gösterir. Terimlerin yan yana gelmesi, birleştirme. Örneğin, h(sen) h(v) birleştirmeyi gösterir h(sen) ile h(v).
^ Bir dil homomorfizminin h boş kelimeyi eşler e boş kelimeye. Dan beri h(e) = h(ee) = h(e)h(e), numara w karakter sayısı h(e) 2 sayısına eşittirw içindeki karakter sayısı h(e)h(e). Bu nedenle w = 0 ve h(e) boş uzunluğa sahiptir.

Alıntılar

^ Fricke, Robert (1897–1912). Vorlesungen über Theorie der automorphen Functionen ölür. B.G. Teubner. OCLC 29857037.
^
Görmek:
- Ritter Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [Sıfır cinsinin benzersiz otomatik biçimleri, Poincaré teoreminin bir revizyonu ve uzantısı]. Mathematische Annalen (Almanca'da). 41: 1–82. doi:10.1007 / BF01443449. S2CID 121524108. Dipnottan s. 22: "Ich, Vorschlage von Hrn'yi okuyacak. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen:" holoedrisch, bezw. hemiedrisch u.s.w. izomorf "die Benennung" izomorfu "auf den Fall des Holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen,… " (Prof. Klein'ın önerisini takiben, hantal ve her zaman tatmin edici olmayan "holohedrik veya hemihedrik, vb. İzomorfik" tanımları yerine, "izomorfik" mezhebini bir durumla sınırlayacağım. holohedrik iki grubun izomorfizmi; aksi halde, bir "homomorfizm" den [ben] söz edeceğim,…)
- Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) ve (2,4,7) gehörenden Dreiecksfunctionen" [Dallanma noktalarına (2,3,7) ve (2,4,7) ait üçgen fonksiyonların aritmetik karakteri hakkında]. Mathematische Annalen (Almanca'da). 41: 443–468. doi:10.1007 / BF01443421. S2CID 120022176. P. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe *) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n uyumsuz Yerine koyma, rationalen ganzen Coefficienten der Determinante 1 begründet. " (Böylece, hemen görüldüğü gibi, Γ grubunun homomorfik bir ilişkisi₍₆₃₎ determinantın rasyonel tam katsayıları ile modulo n uyumsuz sübstitüsyonlar grubuna dayanmaktadır 1.) Dipnot, p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung" meroedrischer Isomorphismus "die sinngemässere" Homomorphismus "." (Bay Klein tarafından daha yakın tarihli konferanslarında ortaya atılan bir kullanımın ardından, daha önceki "merohedral izomorfizm" tanımı yerine daha mantıklı "homomorfizm" yazıyorum.)
^ ^a ^b ^c ^d ^e Birkhoff, Garrett (1967) [1940], Kafes teorisi, American Mathematical Society Colloquium Publications, 25 (3. baskı), Providence, R.I .: Amerikan Matematik Derneği, ISBN 978-0-8218-1025-5, BAY 0598630
^ ^a ^b ^c Stanley N. Burris; H.P. Sankappanavar (2012). Evrensel Cebir Kursu (PDF). ISBN 978-0-9880552-0-9.
^ ^a ^b ^c Mac Lane, Saunders (1971). Çalışan Matematikçi Kategorileri. Matematikte Lisansüstü Metinler. 5. Springer-Verlag. Bölüm I.5'teki Alıştırma 4. ISBN 0-387-90036-5. Zbl 0232.18001.
^ Linderholm, C.E. (1970). Bir grup epimorfizmi örtendir. American Mathematical Monthly, 77(2), 176-177.
^ Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Erban (2001). Hopf Cebiri: Giriş. Saf ve Uygulamalı Matematik. 235. New York, NY: Marcel Dekker. s. 363. ISBN 0824704819. Zbl 0962.16026.
^ Bölüm 17.4, içinde Gunther Schmidt, 2010. İlişkisel Matematik. Cambridge University Press, ISBN 978-0-521-76268-7
^ Seymour Ginsburg, Biçimsel dillerin cebirsel ve otomata teorik özellikleri, Kuzey-Hollanda, 1975, ISBN 0-7204-2506-9,
^ T. Harju, J. Karhumӓki, Morfizmler Biçimsel Diller El Kitabı, Cilt I, düzenleyen G. Rozenberg, A. Salomaa, Springer, 1997, ISBN 3-540-61486-9.

Referanslar

Stanley N. Burris; H.P. Sankappanavar (2012). Evrensel Cebir Kursu (PDF). ISBN 978-0-9880552-0-9.
Mac Lane, Saunders (1971), Çalışan Matematikçi Kategorileri, Matematikte Lisansüstü Metinler, 5, Springer-Verlag, ISBN 0-387-90036-5, Zbl 0232.18001
Fraleigh, John B .; Katz, Victor J. (2003), Soyut Cebirde İlk Ders, Addison-Wesley, ISBN 978-1-292-02496-7

[3] Her zaman olmamakla birlikte çoğu zaman olduğu gibi, her ikisinin de çalışması için aynı sembol ${ displaystyle A}$ ve ${ displaystyle B}$ burada kullanıldı.

[12] ∗, Kleene yıldızı operasyon, Σ^∗ Boş kelime dahil olmak üzere Σ alfabesinden oluşan kelime grubunu gösterir. Terimlerin yan yana gelmesi, birleştirme. Örneğin, h(sen) h(v) birleştirmeyi gösterir h(sen) ile h(v).

[13] Bir dil homomorfizminin h boş kelimeyi eşler e boş kelimeye. Dan beri h(e) = h(ee) = h(e)h(e), numara w karakter sayısı h(e) 2 sayısına eşittirw içindeki karakter sayısı h(e)h(e). Bu nedenle w = 0 ve h(e) boş uzunluğa sahiptir.

[1] Fricke, Robert (1897–1912). Vorlesungen über Theorie der automorphen Functionen ölür. B.G. Teubner. OCLC 29857037.

[2] Görmek:
Ritter Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [Sıfır cinsinin benzersiz otomatik biçimleri, Poincaré teoreminin bir revizyonu ve uzantısı]. Mathematische Annalen (Almanca'da). 41: 1–82. doi:10.1007 / BF01443449. S2CID 121524108. Dipnottan s. 22: "Ich, Vorschlage von Hrn'yi okuyacak. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen:" holoedrisch, bezw. hemiedrisch u.s.w. izomorf "die Benennung" izomorfu "auf den Fall des Holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen,… " (Prof. Klein'ın önerisini takiben, hantal ve her zaman tatmin edici olmayan "holohedrik veya hemihedrik, vb. İzomorfik" tanımları yerine, "izomorfik" mezhebini bir durumla sınırlayacağım. holohedrik iki grubun izomorfizmi; aksi halde, bir "homomorfizm" den [ben] söz edeceğim,…)
Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) ve (2,4,7) gehörenden Dreiecksfunctionen" [Dallanma noktalarına (2,3,7) ve (2,4,7) ait üçgen fonksiyonların aritmetik karakteri hakkında]. Mathematische Annalen (Almanca'da). 41: 443–468. doi:10.1007 / BF01443421. S2CID 120022176. P. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe *) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n uyumsuz Yerine koyma, rationalen ganzen Coefficienten der Determinante 1 begründet. " (Böylece, hemen görüldüğü gibi, Γ grubunun homomorfik bir ilişkisi₍₆₃₎ determinantın rasyonel tam katsayıları ile modulo n uyumsuz sübstitüsyonlar grubuna dayanmaktadır 1.) Dipnot, p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung" meroedrischer Isomorphismus "die sinngemässere" Homomorphismus "." (Bay Klein tarafından daha yakın tarihli konferanslarında ortaya atılan bir kullanımın ardından, daha önceki "merohedral izomorfizm" tanımı yerine daha mantıklı "homomorfizm" yazıyorum.)

[6] Ritter Ernst (1892). "Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze" [Sıfır cinsinin benzersiz otomatik biçimleri, Poincaré teoreminin bir revizyonu ve uzantısı]. Mathematische Annalen (Almanca'da). 41: 1–82. doi:10.1007 / BF01443449. S2CID 121524108. Dipnottan s. 22: "Ich, Vorschlage von Hrn'yi okuyacak. Prof. Klein statt der umständlichen und nicht immer ausreichenden Bezeichnungen:" holoedrisch, bezw. hemiedrisch u.s.w. izomorf "die Benennung" izomorfu "auf den Fall des Holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von "Homomorphismus" sprechen,… " (Prof. Klein'ın önerisini takiben, hantal ve her zaman tatmin edici olmayan "holohedrik veya hemihedrik, vb. İzomorfik" tanımları yerine, "izomorfik" mezhebini bir durumla sınırlayacağım. holohedrik iki grubun izomorfizmi; aksi halde, bir "homomorfizm" den [ben] söz edeceğim,…)

[7] Fricke, Robert (1892). "Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) ve (2,4,7) gehörenden Dreiecksfunctionen" [Dallanma noktalarına (2,3,7) ve (2,4,7) ait üçgen fonksiyonların aritmetik karakteri hakkında]. Mathematische Annalen (Almanca'da). 41: 443–468. doi:10.1007 / BF01443421. S2CID 120022176. P. 466: "Hierdurch ist, wie man sofort überblickt, eine homomorphe *) Beziehung der Gruppe Γ₍₆₃₎ auf die Gruppe der mod. n uyumsuz Yerine koyma, rationalen ganzen Coefficienten der Determinante 1 begründet. " (Böylece, hemen görüldüğü gibi, Γ grubunun homomorfik bir ilişkisi₍₆₃₎ determinantın rasyonel tam katsayıları ile modulo n uyumsuz sübstitüsyonlar grubuna dayanmaktadır 1.) Dipnot, p. 466: "*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung" meroedrischer Isomorphismus "die sinngemässere" Homomorphismus "." (Bay Klein tarafından daha yakın tarihli konferanslarında ortaya atılan bir kullanımın ardından, daha önceki "merohedral izomorfizm" tanımı yerine daha mantıklı "homomorfizm" yazıyorum.)

[Birkhoff.1967-4] Birkhoff, Garrett (1967) [1940], Kafes teorisi, American Mathematical Society Colloquium Publications, 25 (3. baskı), Providence, R.I .: Amerikan Matematik Derneği, ISBN 978-0-8218-1025-5, BAY 0598630

[Burris.Sankappanavar.2012-5] Stanley N. Burris; H.P. Sankappanavar (2012). Evrensel Cebir Kursu (PDF). ISBN 978-0-9880552-0-9.

[workmath-6] Mac Lane, Saunders (1971). Çalışan Matematikçi Kategorileri. Matematikte Lisansüstü Metinler. 5. Springer-Verlag. Bölüm I.5'teki Alıştırma 4. ISBN 0-387-90036-5. Zbl 0232.18001.

[7] Linderholm, C.E. (1970). Bir grup epimorfizmi örtendir. American Mathematical Monthly, 77(2), 176-177.

[8] Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Erban (2001). Hopf Cebiri: Giriş. Saf ve Uygulamalı Matematik. 235. New York, NY: Marcel Dekker. s. 363. ISBN 0824704819. Zbl 0962.16026.

[9] Bölüm 17.4, içinde Gunther Schmidt, 2010. İlişkisel Matematik. Cambridge University Press, ISBN 978-0-521-76268-7

[10] Seymour Ginsburg, Biçimsel dillerin cebirsel ve otomata teorik özellikleri, Kuzey-Hollanda, 1975, ISBN 0-7204-2506-9,

[11] T. Harju, J. Karhumӓki, Morfizmler Biçimsel Diller El Kitabı, Cilt I, düzenleyen G. Rozenberg, A. Salomaa, Springer, 1997, ISBN 3-540-61486-9.

[1]

[2]

[not 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[not 2]

[not 3]