Lévy uçuşu - Lévy flight
Bir Lévy uçuşu, Fransız matematikçi Paul Lévy, bir rastgele yürüyüş adım uzunluklarının bir Lévy dağılımı, bir olasılık dağılımı yani ağır kuyruklu. Birden büyük boyutlu bir alanda yürüyüş olarak tanımlandığında, atılan adımlar izotropik rastgele yönler.
"Lévy uçuşu" terimi, Benoît Mandelbrot,[1] bunu adım boyutlarının dağılımının belirli bir tanımı için kullanan. O terimi kullandı Cauchy uçuşu adım boyutlarının dağılımının bir olduğu durum için Cauchy dağılımı,[2] ve Rayleigh uçuşu dağıtımın bir normal dağılım[3] (bu, ağır kuyruklu bir olasılık dağılımına örnek değildir).
Daha sonra araştırmacılar, rastgele yürüyüşün sürekli bir uzay yerine ayrı bir ızgara üzerinde gerçekleştiği durumları da içerecek şekilde "Lévy uçuşu" teriminin kullanımını genişletti.[4][5]
Mandelbrot'un "Lévy uçuşu" terimini kullandığı özel durum[1] tarafından tanımlanır hayatta kalan işlevi (genellikle hayatta kalma işlevi olarak bilinir) adım boyutlarının dağılımının, U, olmak[6]
Buraya D ile ilgili bir parametredir Fraktal boyut ve dağıtım, belirli bir durumdur Pareto dağılımı.
Özellikleri
Lévy uçuşları, yapım gereği, Markov süreçleri. Kademeli büyüklüğün genel dağılımları için, güç benzeri koşulu tatmin etmek için, rastgele yürüyüşün başlangıcından olan mesafe, çok sayıda adımdan sonra, kararlı dağıtım genelleştirilmiş nedeniyle Merkezi Limit Teoremi, birçok sürecin Lévy uçuşları kullanılarak modellenmesini sağlar.
Bir Levy uçuşuna maruz kalan parçacıkların olasılık yoğunlukları, genellikle Brownian hareketini modellemek için kullanılan Fokker-Planck denkleminin genelleştirilmiş bir versiyonu kullanılarak modellenebilir. Denklem, kesirli türevlerin kullanılmasını gerektirir. Simetrik olasılık dağılımına sahip atlama uzunlukları için denklem, Riesz kesirli türevi açısından basit bir biçim alır. Bir boyutta denklem şu şekilde okunur
γ difüzyon sabitine benzer bir sabit olduğunda, α kararlılık parametresidir ve f (x, t) potansiyeldir. Riesz türevi, Fourier Dönüşümü açısından anlaşılabilir.
Bu, birden çok boyuta kolayca genişletilebilir.
Lévy uçuşunun bir diğer önemli özelliği de, uçuşunki hariç tüm durumlarda farklılaşan varyanslardır. α = 2, yani Brown hareketi. Genel olarak, dağılımın θ fraksiyonel momenti, eğer α ≤ θ. Ayrıca,
Adım uzunluklarının üstel ölçeklendirilmesi, Lévy uçuşlarına ölçek değişmezi Emlak,[kaynak belirtilmeli ] ve kümeleme sergileyen verileri modellemek için kullanılırlar.[kaynak belirtilmeli ]
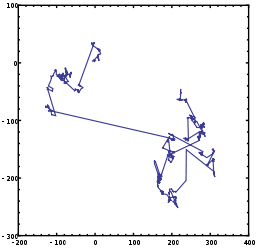

Başvurular
Bir Lévy uçuşunun tanımı, ilgili matematikten kaynaklanır. kaos teorisi ve rastgele veya sözde rastgele doğa olayları için stokastik ölçüm ve simülasyonlarda kullanışlıdır. Örnekler şunları içerir: deprem veri analizi, Finansal matematik, kriptografi sinyal analizi ve birçok uygulama astronomi, Biyoloji, ve fizik.
Başka bir uygulama ise Lévy uçuş arama hipotezi. Köpekbalıkları ve diğer okyanus avcıları yiyecek bulamadıklarında terk ederler. Brown hareketi, Lévy uçuşu için dönen gaz moleküllerinde görülen rastgele hareket - türbülanslı sıvılarda bulunan uzun yörüngeler ve kısa, rastgele hareketlerin bir karışımı. Araştırmacılar, dahil olmak üzere Atlantik ve Pasifik Okyanuslarındaki 14 okyanus yırtıcı türünden 55 veri kaydedici etiketli hayvanda 5.700 günde kaydedilen 12 milyondan fazla hareketi analiz etti. ipeksi köpekbalıkları, sarı yüzgeçli ton balığı, mavi marlin ve kılıç balığı. Veriler, Brownian hareketi ile serpiştirilmiş Lévy uçuşlarının, hayvanların avlanma modellerini tanımlayabileceğini gösterdi.[7][8][9][10] Kuşlar ve diğer hayvanlar[11] (insanlar dahil)[12] Lévy uçuşu kullanılarak modellenen yolları takip edin (örneğin yiyecek ararken).[13] Biyolojik uçuş verileri, optimal Lévy yürüyüşlerinde yakınsamak için ölçekler arasında büyüyen kompozit bağlantılı rastgele yürüyüşler gibi diğer modeller tarafından da taklit edilebilir.[13] Kompozit Brownian yürüyüşleri teorik olarak optimal Lévy yürüyüşlerine ince bir şekilde ayarlanabilir, ancak bunlar çoğu manzara türünde Lévy araması kadar verimli değildir, bu da Lévy yürüyüş özellikleri için seçim baskısının çok ölçekli normal yayılma modellerinden daha olası olduğunu düşündürür.[14]
Bir ağda verimli yönlendirme, belirli alfa değerlerine sahip bir Levy uçuş uzunluğu dağılımına sahip bağlantılar ile gerçekleştirilebilir.[4][5]
Ayrıca bakınız
- Yağ kuyruklu dağılım
- Ağır kuyruklu dağılım
- Lévy süreci
- Lévy alpha-kararlı dağılım
- Lévy uçuş arama hipotezi
Notlar
- ^ a b Mandelbrot (1982), s. 289)
- ^ Mandelbrot (1982), s. 290)
- ^ Mandelbrot (1982), s. 288)
- ^ a b J. M. Kleinberg (2000). "Küçük bir dünyada navigasyon". Doğa. 406 (6798): 845. Bibcode:2000Natur.406..845K. doi:10.1038/35022643. PMID 10972276.
- ^ a b Li, G .; Reis, S. D. S .; Moreira, A. A .; Havlin, S.; Stanley, H. E.; Andrade, J. S. (2010-01-06). "Optimal Ulaşım Ağları için Tasarım İlkelerine Doğru" (PDF). Fiziksel İnceleme Mektupları. 104 (1): 018701. arXiv:0908.3869. Bibcode:2010PhRvL.104a8701L. doi:10.1103 / PhysRevLett.104.018701. ISSN 0031-9007. PMID 20366398.
- ^ Mandelbrot (1982), s. 294)
- ^ Sims, David W .; Southall, Emily J .; Humphries, Nicolas E .; Hays, Graeme C .; Bradshaw, Corey J. A .; Pitchford, Jonathan W .; James, Alex; Ahmed, Muhammed Z .; Brierley, Andrew S .; Hindell, Mark A .; Morritt, David; Musyl, Michael K .; Righton, David; Shepard, Emily L. C .; Wearmouth, Victoria J .; Wilson, Rory P .; Witt, Matthew J .; Metcalfe, Julian D. (2008). "Deniz avcısı arama davranışının ölçeklendirme yasaları". Doğa. 451 (7182): 1098–1102. Bibcode:2008Natur.451.1098S. doi:10.1038 / nature06518. PMID 18305542.
- ^ Humphries, Nicolas E .; Queiroz, Nuno; Dyer, Jennifer R. M .; Pade, Nicolas G .; Musyl, Michael K .; Schaefer, Kurt M .; Fuller, Daniel W .; Brunnschweiler, Juerg M .; Doyle, Thomas K .; Houghton, Jonathan D. R .; Hays, Graeme C .; Jones, Catherine S .; Noble, Leslie R .; Wearmouth, Victoria J .; Southall, Emily J .; Sims, David W. (2010). "Çevresel bağlam, denizdeki avcıların Lévy ve Brownian hareket modellerini açıklıyor" (PDF). Doğa. 465 (7301): 1066–1069. Bibcode:2010Natur.465.1066H. doi:10.1038 / nature09116. PMID 20531470.
- ^ Witze, Alexandra. "Köpekbalıklarının Matematik Becerileri Vardır". discovery.com. Alındı 22 Şubat 2013.
- ^ Dacey, James. "Köpekbalıkları Lévy uçuşlarıyla avlanır". physicsworld.com. Alındı 22 Şubat 2013.
- ^ Viswanathan, G. M .; Buldyrev, S. V .; Havlin, Shlomo; da Luz, M. G. E .; Raposo, E. P .; Stanley, H. E. (1999). "Rastgele aramaların başarısını optimize etme". Doğa. 401 (6756): 911–914. Bibcode:1999Natur.401..911V. doi:10.1038/44831. PMID 10553906.
- ^ Reynolds, Gretchen (1 Ocak 2014). "Dünyamızı Kuşlar Gibi Gezmek ve bazı yazarlar arıların hareketini iddia ettiler". New York Times.
- ^ a b Sims, David W.; Reynolds, Andrew M .; Humphries, Nicholas E .; Southall, Emily J .; Wearmouth, Victoria J .; Metcalfe, Brett; Twitchett, Richard J. (29 Temmuz 2014). "İz fosillerinde hiyerarşik rastgele gezinme ve optimal arama davranışının kaynağı". Ulusal Bilimler Akademisi Bildiriler Kitabı. 111 (30): 11073–11078. doi:10.1073 / pnas.1405966111. ISSN 0027-8424. PMC 4121825. PMID 25024221.
- ^ Humphries, N.E .; Sims, D.W. (2014). "Optimal yiyecek arama stratejileri: Lévy, çok çeşitli koşullar altında denge araştırması ve yama istismarını yürütür" (PDF). Teorik Biyoloji Dergisi. 358: 179–193. doi:10.1016 / j.jtbi.2014.05.032. PMID 24882791.
Referanslar
- Mandelbrot, Benoit B. (1982). Doğanın Fraktal Geometrisi (Güncellendi ve büyültüldü.). New York: W. H. Freeman. ISBN 0-7167-1186-9. OCLC 7876824.
daha fazla okuma
- Viswanathan, G .; Bartumeus, F .; v. Buldyrev, S .; Katalanca, J .; Fulco, U .; Havlin, S .; Da Luz, M .; Lyra, M .; Raposo, E .; Eugene Stanley, H. (2002). "Biyolojik olaylarda Lévy uçuş rastgele araştırmaları". Physica A: İstatistiksel Mekanik ve Uygulamaları. 314 (1–4): 208–213. Bibcode:2002PhyA..314..208V. doi:10.1016 / S0378-4371 (02) 01157-3.
- Viswanathan, G .; Afanasyev, V .; Buldyrev, S .; Havlin, S .; Daluz, M .; Raposo, E .; Stanley, H. (2000). "Rastgele aramalarda Lévy uçuşları". Physica A: İstatistiksel Mekanik ve Uygulamaları. 282 (1–2): 1–12. Bibcode:2000PhyA..282 .... 1V. doi:10.1016 / S0378-4371 (00) 00071-6.
- Cheng, Z .; Savit, R. (1987). "Levy uçuşlarında fraktal ve fraktal olmayan davranış" (PDF). Matematiksel Fizik Dergisi. 28 (3): 592. Bibcode:1987JMP .... 28..592C. doi:10.1063/1.527644. hdl:2027.42/70735.
- Shlesinger, Michael F .; Klafter, Joseph; Zumofen, Gert (Aralık 1999). "Brown hareketinin üstünde, altında ve ötesinde" (PDF). Amerikan Fizik Dergisi. 67 (12): 1253–1259. Bibcode:1999AmJPh..67.1253S. doi:10.1119/1.19112. Arşivlenen orijinal (PDF) 2012-03-28 tarihinde.



![{ displaystyle F_ {k} sol [{ frac { kısmi ^ { alfa} varphi (x, t)} { kısmi | x | ^ { alfa}}} sağ] = - | k | ^ { alfa} F_ {k} [ varphi (x, t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2991424fe3f2d2284bd5e8c81d1a70845503c83)



