Gerçek koordinat alanı - Real coordinate space
Bu makale için ek alıntılara ihtiyaç var doğrulama. (Nisan 2013) (Bu şablon mesajını nasıl ve ne zaman kaldıracağınızı öğrenin) |

İçinde matematik, bir gerçek koordinat alanı nın-nin boyut n, yazılı Rn (/ɑːrˈɛn/ ar-TR ) veya ℝn, bir koordinat alanı üzerinde gerçek sayılar. Bu, bunun set olduğu anlamına gelir nikili gerçek sayıların (dizileri n gerçek sayılar). Bileşen bazlı toplama ve skaler çarpma ile, bu bir gerçek vektör uzayı.
Tipik olarak Kartezyen koordinatları bir öğesinin Öklid uzayı gerçek bir koordinat alanları oluşturur. Bu ismini açıklıyor koordinat alanı ve gerçek şu ki geometrik koordinat alanlarıyla çalışırken genellikle terimler kullanılır. Örneğin, R2 bir uçak.
Koordinat alanları yaygın olarak kullanılmaktadır. geometri ve fizik, öğeleri Öklid uzaylarında noktaların bulunmasına ve onlarla hesaplamaya izin verdiği için.
Tanım ve yapılar
Herhangi doğal sayı n, Ayarlamak Rn hepsinden oluşur n-demetler nın-nin gerçek sayılar (R). "nboyutlu gerçek uzay "veya" gerçek n-Uzay".
Bir öğesi Rn bu nedenle bir n-tuple ve yazılır
her biri nerede xben gerçek bir sayıdır. Yani, içinde Çok değişkenli hesap, alan adı bir birkaç gerçek değişkenin işlevi ve gerçek bir ortak etki alanı vektör değerli fonksiyon vardır alt kümeler nın-nin Rn bazı n.
Gerçek n-space'in birkaç ek özelliği vardır, özellikle:
- İle bileşensel ek ve skaler çarpım, bu bir gerçek vektör uzayı. Her nboyutlu gerçek vektör uzayı izomorf ona.
- İle nokta ürün (bileşenlerin terim çarpımına göre terim toplamı), bir iç çarpım alanı. Her n-boyutlu gerçek iç çarpım uzay ona izomorfiktir.
- Her iç çarpım alanı gibi, bir topolojik uzay ve bir topolojik vektör uzayı.
- Bu bir Öklid uzayı ve gerçek afin boşluk ve her Öklid veya afin uzay ona izomorfiktir.
- O bir analitik manifold ve hepsinin prototipi olarak düşünülebilir manifoldlar, tanım gereği, bir manifold, her noktanın yakınında, bir alt küme aç nın-nin Rn.
- O bir cebirsel çeşitlilik, ve hepsi gerçek cebirsel çeşitlilik alt kümesidir Rn.
Bu özellikleri ve yapıları Rn matematiğin hemen hemen tüm alanlarında ve bunların uygulama alanlarında, örneğin İstatistik, olasılık teorisi ve birçok bölümü fizik.
Birkaç değişkenli bir fonksiyonun alanı
Herhangi bir işlev f(x1, x2, … , xn) nın-nin n gerçek değişkenler bir fonksiyon olarak düşünülebilir Rn (yani Rn onun gibi alan adı ). Gerçeğin kullanımı n-uzay, ayrı ayrı ele alınan birkaç değişken yerine, gösterimi basitleştirebilir ve makul tanımlar önerebilir. Şunun için düşünün n = 2, bir işlev bileşimi aşağıdaki biçimde:
fonksiyonlar nerede g1 ve g2 vardır sürekli. Eğer
- ∀x1 ∈ R : f(x1, ·) süreklidir (tarafından x2)
- ∀x2 ∈ R : f(·, x2) süreklidir (tarafından x1)
sonra F mutlaka sürekli değildir. Süreklilik daha güçlü bir durumdur: süreklilik f doğal olarak R2 topoloji (Aşağıda tartışılmıştır ), olarak da adlandırılır çok değişkenli süreklilikkompozisyonun devamlılığı için yeterli olan F.
Bu bölüm genişlemeye ihtiyacı var. Yardımcı olabilirsiniz ona eklemek. (Nisan 2013) |
Vektör alanı
Koordinat alanı Rn oluşturur n-boyutlu vektör alanı üzerinde alan yapısının eklenmesiyle gerçek sayıların doğrusallık ve genellikle hala belirtilir Rn. İşlemler Rn bir vektör uzayı olarak tipik olarak tanımlanır
sıfır vektör tarafından verilir
ve toplamsal ters vektörün x tarafından verilir
Bu yapı önemlidir çünkü herhangi bir nboyutlu gerçek vektör uzayı, vektör uzayına izomorfiktir Rn.
Matris gösterimi
Standart olarak matris gösterim, her bir öğesi Rn tipik olarak şöyle yazılır kolon vektörü
ve bazen bir satır vektör:
Koordinat alanı Rn daha sonra hepsinin alanı olarak yorumlanabilir n × 1 sütun vektörleri veya tümü 1 × n satır vektörleri sıradan matris işlemleriyle toplama ve skaler çarpım.
Doğrusal dönüşümler itibaren Rn -e Rm daha sonra şöyle yazılabilir m × n elemanlarına etki eden matrisler Rn üzerinden ayrıldı çarpma (öğeleri ne zaman Rn sütun vektörleridir) ve öğelerinde Rm doğru çarpma yoluyla (satır vektörleri olduklarında). Sol çarpma formülü, özel bir durum matris çarpımı, dır-dir:
Herhangi bir doğrusal dönüşüm bir sürekli işlev (görmek altında ). Ayrıca, bir matris bir haritayı aç itibaren Rn -e Rm ancak ve ancak matrisin sıralaması eşittir m.
Standart temel
Koordinat alanı Rn standart bir temel ile gelir:
Bunun bir temel olduğunu görmek için, rastgele bir vektörün Rn formda benzersiz şekilde yazılabilir
Geometrik özellikler ve kullanımlar
Oryantasyon
Gerçeği gerçek sayılar diğerlerinin aksine alanlar, oluşturmak sıralı alan verir yönlendirme yapısı açık Rn. Hiç tam dereceli doğrusal haritası Rn kendisine bağlı olarak alanın yönünü ya korur ya da tersine çevirir. işaret of belirleyici matrisinin. Eğer biri permüteler koordinatlar (veya başka bir deyişle, temelin unsurları), ortaya çıkan yönelim, permütasyon paritesi.
Diffeomorfizmler nın-nin Rn veya içindeki alanlar sıfırdan kaçınmak için erdemleri gereği Jacobian, aynı zamanda yönü koruyan ve yönü tersine çeviren olarak sınıflandırılır. Teorisi için önemli sonuçları vardır. diferansiyel formlar, uygulamaları şunları içerir elektrodinamik.
Bu yapının bir başka tezahürü, nokta yansıması içinde Rn bağlı olarak farklı özelliklere sahiptir eşitliği n. Çift için n tuhaf ise yönelimi korur n tersine çevrilir (ayrıca bakınız uygunsuz rotasyon ).
Afin uzay
Rn afin uzay olarak anlaşılan aynı uzaydır, burada Rn vektör uzayı olarak hareketler tarafından çeviriler. Tersine, bir vektör bir "fark iki nokta arasında ", genellikle yönlendirilmiş bir çizgi segmenti iki noktayı birleştirmek. Ayrım olmadığını söylüyor kanonik nerede seçim Menşei afine gitmeli n-space, çünkü herhangi bir yere çevrilebilir.
Dışbükeylik

Gerçek bir vektör uzayında, örneğin Rnbir dışbükey tanımlanabilir koni, hepsini içeren negatif olmayan vektörlerinin doğrusal kombinasyonları. Afin bir uzayda karşılık gelen kavram bir dışbükey küme sadece izin verir dışbükey kombinasyonlar (toplamı 1 olan negatif olmayan doğrusal kombinasyonlar).
Dilinde evrensel cebir, vektör uzayı evrensel vektör uzayı üzerindeki bir cebirdir R∞ vektörlerin sonlu toplamlarına karşılık gelen sonlu katsayı dizileri, bir afin uzay bu uzaydaki evrensel afin hiper düzlem üzerinde bir cebir iken (1'e toplanan sonlu dizilerin), bir koni, evrensel üzerinde bir cebirdir. orthant (negatif olmayan sayıların sonlu dizilerinin) ve bir dışbükey küme, evrensel üzerinde bir cebirdir. basit (1'e toplamı olan negatif olmayan sayıların sonlu dizilerinin). Bu, aksiyomları "koordinatlar üzerinde (olası) kısıtlamalara sahip toplamlar" açısından geometriye sokar.
Dışbükey analizden elde edilen diğer bir kavram, dışbükey işlev itibaren Rn ile tanımlanan gerçek sayılara eşitsizlik dışbükey kombinasyonundaki değeri arasında puan ve bu noktalardaki aynı katsayılara sahip değerlerin toplamı.
Öklid uzayı
tanımlar norm |x| = √x ⋅ x vektör uzayında Rn. Her vektörün kendi Öklid normu, sonra herhangi bir nokta çifti için mesafe
tanımlanır, bir metrik uzay yapı üzerinde Rn afin yapısına ek olarak.
Vektör uzayı yapısına gelince, iç çarpım ve Öklid mesafesinin genellikle içinde var olduğu varsayılır. Rn özel açıklamalar olmadan. Ancak gerçek n-space ve bir Öklid n-space, kesinlikle farklı nesnelerdir. Herhangi bir Öklid n-space'de koordinat sistemi iç çarpım ve Öklid mesafesinin yukarıda gösterilen forma sahip olduğu, Kartezyen. Ama var birçok Öklid uzayında kartezyen koordinat sistemleri.
Tersine, Öklid metriği için yukarıdaki formül, standart Öklid yapısı Rnama bu mümkün olan tek şey değil. Aslında herhangi biri pozitif tanımlı ikinci dereceden form q kendi "mesafesini" tanımlar √q(x − y), ancak Öklid olandan çok da farklı değildir.
Metrikte böyle bir değişiklik, metriğin bazı özelliklerini korur, örneğin bir metrik olma özelliğini tam metrik uzay Bu aynı zamanda herhangi bir tam aşamalı doğrusal dönüşümün Rnveya onun afin dönüşüm, mesafeleri bazı sabit ayarlardan daha fazla büyütmez C2ve mesafeleri daha küçük yapmaz 1 ∕ C1 kez, sabit sonlu sayı kat daha küçük.[açıklama gerekli ]
Metrik fonksiyonların yukarıda belirtilen eşdeğerliği, eğer √q(x − y) ile değiştirilir M(x − y), nerede M herhangi bir dışbükey pozitif mi homojen işlev derece 1, yani a vektör normu (görmek Minkowski mesafesi faydalı örnekler için). Bu gerçek nedeniyle, herhangi bir "doğal" metrik Rn Öklid metriğinden özellikle farklı değildir, Rn her zaman bir Öklidden ayırt edilmez n-profesyonel matematiksel çalışmalarda bile boşluk.
Cebirsel ve diferansiyel geometride
Bir tanımı olmasına rağmen manifold model alanının olmasını gerektirmez Rn, bu seçim en yaygın ve neredeyse tek seçenektir. diferansiyel geometri.
Diğer taraftan, Whitney yerleştirme teoremleri herhangi bir gerçek olduğunu belirtin ayırt edilebilir mboyutlu manifold olabilir gömülü içine R2m.
Bu bölüm genişlemeye ihtiyacı var. Yardımcı olabilirsiniz ona eklemek. (Nisan 2013) |
Diğer görünüşler
Üzerinde düşünülen diğer yapılar Rn birini dahil et sözde Öklid uzayı, semplektik yapı (hatta n), ve iletişim yapısı (garip n). Tüm bu yapılar, koordinatsız bir şekilde tanımlanabilmesine rağmen, koordinatlarda standart (ve oldukça basit) formları kabul eder.
Rn aynı zamanda gerçek bir vektör alt uzayıdır Cn değişmeyen karmaşık çekim; Ayrıca bakınız karmaşıklaştırma.
R'deki politoplarn
Üç aile var politoplar basit temsilleri olan Rn herhangi biri için boşluk nve herhangi bir afin koordinat sistemini gerçek bir şekilde görselleştirmek için kullanılabilir n-Uzay. Bir hiperküp koordinatları var (x1, x2, … , xn) her biri nerede xk yalnızca iki değerden birini alır, tipik olarak 0 veya 1. Bununla birlikte, 0 ve 1 yerine herhangi iki sayı seçilebilir, örneğin −1 ve 1. Bir nhiperküp, kartezyen ürünü olarak düşünülebilir. n özdeş aralıklar (benzeri birim aralığı [0,1]) gerçek hatta. Bir nboyutlu bir alt küme ile tanımlanabilir sistemi 2n eşitsizlikler:
| (için [0,1]) | (için [−1,1]) |
Her köşesi çapraz politop bazıları için k, xk eşit koordinat ±1 ve diğer tüm koordinatlar 0'a eşittir (öyle ki kinci standart temel vektör kadar işaret ). Bu bir ikili politop hiperküp. Bir nboyutsal alt küme, tek bir eşitsizlikle tanımlanabilir. mutlak değer operasyon:
ancak bu bir sistemle ifade edilebilir 2n doğrusal eşitsizlikler de.
Basit bir şekilde numaralandırılabilir koordinatlara sahip üçüncü politop, standart tek taraflı, kimin köşeleri n standart temel vektörler ve köken (0, 0, … , 0). Bir nboyutsal alt küme bir sistemle tanımlanır n + 1 doğrusal eşitsizlikler:
Tüm "≤" harflerinin "<" ile değiştirilmesi, bu politopların iç kısımlarını verir.
Topolojik özellikler
topolojik yapı nın-nin Rn (aranan standart topoloji, Öklid topolojisiveya olağan topoloji) sadece elde edilemez Kartezyen üründen. Aynı zamanda şununla aynıdır: doğal topoloji neden oldu Yukarıda tartışılan öklid metriği: bir küme açık Öklid topolojisinde ancak ve ancak içerir açık top her noktasının etrafında. Ayrıca, Rn bir doğrusal topolojik uzay (görmek doğrusal haritaların sürekliliği Yukarıdaki) ve doğrusal yapısıyla uyumlu yalnızca bir olası (önemsiz olmayan) topoloji vardır. Birçok açık doğrusal harita olduğu için Rn kendisine olmayan izometriler, üzerinde birçok Öklid yapısı olabilir Rn aynı topolojiye karşılık gelen. Aslında doğrusal yapıya çok da bağlı değildir: doğrusal olmayan birçok diffeomorfizmler (ve diğer homeomorfizmler) Rn kendi üzerine veya Öklid açık top gibi parçalarına veya bir hiperküpün içi ).
Rn var topolojik boyut nTopolojisinde önemli bir sonuç Rnbu yüzeysel olmaktan çok uzaktır Brouwer 's etki alanının değişmezliği. Herhangi bir alt kümesi Rn (onunla alt uzay topolojisi ) yani homomorfik başka bir açık alt kümeye Rn kendisi açık. Bunun acil bir sonucu şudur: Rm değil homomorfik -e Rn Eğer m ≠ n - yine de kanıtlaması zor olan sezgisel olarak "bariz" bir sonuç.
Topolojik boyuttaki farklılığa ve naif bir algının tersine, daha küçük boyutlu bir haritayı haritalamak mümkündür.[açıklama gerekli ] gerçek alan sürekli ve kesin olarak üstüne Rn. Sürekli (pürüzsüz olmasa da) boşluk doldurma eğrisi (bir resim R1) mümkün.[açıklama gerekli ]
Örnekler
| Boş kolon vektörü, tek unsuru R0 |
 |
| R1 |
n ≤ 1
Vakalar 0 ≤ n ≤ 1 yeni bir şey teklif etmeyin: R1 ... gerçek çizgi, buna karşılık R0 (boş sütun vektörünü içeren alan) bir Singleton olarak anlaşıldı sıfır vektör uzayı. Ancak bunları şu şekilde eklemekte fayda var: önemsiz farklı tanımlayan kuram vakaları n.
n = 2
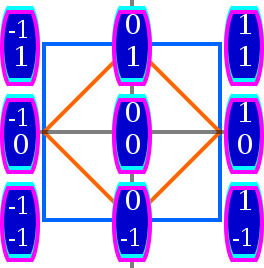
Bu bölüm genişlemeye ihtiyacı var. Yardımcı olabilirsiniz ona eklemek. (Nisan 2013) |
n = 3

Bu bölüm genişlemeye ihtiyacı var. Yardımcı olabilirsiniz ona eklemek. (Nisan 2013) |
n = 4

R4 gerçeği kullanılarak hayal edilebilir 16 puan (x1, x2, x3, x4)her biri nerede xk 0 veya 1, a'nın köşeleridir tesseract (resimde), 4-hiperküp (bkz. yukarıda ).
İlk büyük kullanım R4 bir boş zaman model: üç uzamsal koordinat artı bir geçici. Bu genellikle şununla ilişkilidir: görecelilik teorisi bu tür modeller için dört boyut kullanılmasına rağmen Galilei. Teori seçimi, farklı bir yapıya yol açar: Galile göreliliği t koordinat ayrıcalıklıdır, ancak Einstein'ın göreliliğinde değildir. Özel görelilik, Minkowski alanı. Genel görelilik, şu şekilde düşünülebilecek kavisli uzayları kullanır. R4 Birlikte eğri metrik çoğu pratik amaç için. Bu yapıların hiçbiri (pozitif-tanımlı) sağlamaz metrik açık R4.
Öklid R4 matematikçilerin de ilgisini çeker, örneğin kuaterniyonlar 4 boyutlu gerçek cebir kendilerini. Görmek 4 boyutlu Öklid uzayında dönme bazı bilgiler için.
Diferansiyel geometride, n = 4 tek durum Rn standart dışı olduğunu kabul ediyor diferansiyel yapı: görmek egzotik R4.
Normlar açık Rn
Birçok norm tanımlanabilir. vektör alanı Rn. Bazı yaygın örnekler
- p-norm, tarafından tanımlanan hepsi için Rn nerede pozitif bir tamsayıdır. Dava çok önemli çünkü tam olarak Öklid normu.
- -norm veya maksimum norm, tarafından tanımlanan hepsi için Rn. Bu, hepsinin sınırıdır p-normları: .
Gerçekten şaşırtıcı ve faydalı bir sonuç, her normun Rn dır-dir eşdeğer. Bu, iki keyfi norm anlamına gelir ve açık Rn her zaman pozitif gerçek sayılar bulabilirsin , öyle ki
hepsi için Rn.
Bu bir denklik ilişkisi tüm normlar setinde Rn. Bu sonuçla, bir vektör dizisinin, Rn ile birleşir ancak ve ancak yakınsarsa .
İşte bu sonucun kanıtının nasıl görünebileceğinin bir taslağı:
Yüzünden denklik ilişkisi her normun üzerinde olduğunu göstermek yeterlidir Rn eşdeğerdir Öklid normu . İzin Vermek keyfi bir norm olmak Rn. İspat iki aşamaya bölünmüştür:
- Var olduğunu gösteriyoruz , öyle ki hepsi için Rn. Bu adımda, her birinin Rn standardın doğrusal bir kombinasyonu olarak temsil edilebilir temel: . Sonra Cauchy-Schwarz eşitsizliği , nerede .
- Şimdi bir bulmalıyız , öyle ki hepsi için Rn. Böyle bir şey olmadığını varsayın . O zaman herkes için var a Rn, öyle ki . İkinci bir sıra tanımlayın tarafından . Bu dizi sınırlı çünkü . Yani yüzünden Bolzano-Weierstrass teoremi yakınsak bir alt dizi var limitli Rn. Şimdi bunu gösteriyoruz fakat bu bir çelişkidir. Bu , Çünkü ve , yani . Bu ima eder , yani . Diğer taraftan , Çünkü . Bu asla doğru olamaz, bu yüzden varsayım yanlıştı ve böyle bir .
Ayrıca bakınız
- Üstel nesne, üst simge notasyonunun teorik açıklaması için
- Gerçek yansıtmalı alan
Dipnotlar
Referanslar
- Kelley, John L. (1975). Genel Topoloji. Springer-Verlag. ISBN 0-387-90125-6.
- Munkres James (1999). Topoloji. Prentice-Hall. ISBN 0-13-181629-2.



















![{ displaystyle || { textbf {x}} || _ {p}: = { sqrt [{p}] { toplam _ {i = 1} ^ {n} | x_ {i} | ^ {p }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bda5105bdb8d31bd40862ea8fe1ee42f85fb1cf6)





![{ displaystyle || { textbf {x}} || _ { infty} = lim limitler _ {p to infty} { sqrt [{p}] { sum _ {i = 1} ^ {n} | x_ {i} | ^ {p}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3da3da3bd883619a3ad4789537e4907b26be29e3)





























