E7 (matematik) - E7 (mathematics)
| Cebirsel yapı → Grup teorisi Grup teorisi |
|---|
 |
Sonsuz boyutlu Lie grubu
|
| Lie grupları |
|---|
 |
|
İçinde matematik, E7 yakından ilişkili birkaç kişinin adıdır Lie grupları, doğrusal cebirsel gruplar veya onların Lie cebirleri e7hepsi 133 boyutuna sahip; aynı gösterim E7 karşılık gelen için kullanılır kök kafes, hangisi sıra 7. E tanımı7 dan geliyor Cartan-Öldürme sınıflandırması kompleksin basit Lie cebirleri A etiketli dört sonsuz diziye girenn, Bn, Cn, Dn, ve beş istisnai durum etiketli E6, E7, E8, F4, ve G2. E7 cebir bu nedenle beş istisnai durumdan biridir.
(Birleşik) karmaşık formun, kompakt gerçek formun veya E'nin herhangi bir cebirsel versiyonunun temel grubu7 ... döngüsel grup Z/2Z, ve Onun dış otomorfizm grubu ... önemsiz grup. Onun boyutu temel temsil 56'dır.
Gerçek ve karmaşık formlar
E tipi benzersiz bir karmaşık Lie cebiri vardır7karmaşık boyut 133 grubuna karşılık gelir. Karmaşık eşlenik Lie grubu E7 nın-nin karmaşık boyut 133, gerçek boyut 266'nın basit bir gerçek Lie grubu olarak düşünülebilir. Bu, temel gruba sahiptir. Z/2Z, maksimal kompakt E'nin kompakt formunu (aşağıya bakın) alt gruplandırın7ve karmaşık konjugasyon ile oluşturulan 2. dereceden bir dış otomorfizm grubuna sahiptir.
E tipi karmaşık Lie grubunun yanı sıra7, Lie cebirinin dört gerçek formu ve buna uygun olarak önemsiz merkezli grubun dört gerçek formu vardır (bunların tümü cebirsel bir çift örtülüdür ve üçü başka cebirsel olmayan kaplamalara sahiptir, daha fazla gerçek formlar verir). 133 gerçek boyutu aşağıdaki gibidir:
- Temel gruba sahip kompakt form (genellikle başka bir bilgi verilmemişse kastedilen) Z/2Z ve önemsiz bir dış otomorfizm grubuna sahiptir.
- Bölünmüş form, EV (veya E7(7)), maksimum kompakt alt grubu SU (8) / {± 1}, 4. dereceden temel grup döngüsü ve 2. dereceden dış otomorfizm grubuna sahip.
- EVI (veya E7(-5)), maksimum kompakt alt grubu SU (2) · SO (12) / (merkez), 4. dereceden döngüsel olmayan temel grup ve önemsiz dış otomorfizm grubuna sahip.
- EVII (veya E7(-25)), maksimal kompakt alt grubu olan SO (2) · E6/ (merkez), sonsuz döngüsel temel grup ve 2. dereceden dış otomorfizm grubu.
Basit Lie cebirlerinin gerçek formlarının tam listesi için bkz. basit Lie gruplarının listesi.
E'nin kompakt gerçek formu7 ... izometri grubu 64 boyutlu olağanüstü kompakt Riemann simetrik uzay EVI (Cartan'da sınıflandırma ). Gayri resmi olarak "kuateroktonyonik projektif düzlem "çünkü bir cebir kullanılarak inşa edilebilir. kuaterniyonlar ve sekizlik ve aynı zamanda bir Rosenfeld projektif düzlem bir yansıtmalı düzlemin olağan aksiyomlarına uymasa da. Bu, sistematik olarak bilinen bir yapı kullanılarak görülebilir. sihirli kare, Nedeniyle Hans Freudenthal ve Jacques Göğüsleri.
Göğüsler-Koecher inşaatı E formlarını üretir7 Lie cebiri Albert cebirleri, 27 boyutlu olağanüstü Ürdün cebirleri.
E7 cebirsel bir grup olarak
Bir vasıtasıyla Chevalley temeli Lie cebiri için E tanımlanabilir7 tamsayılar üzerinde ve dolayısıyla herhangi bir değişmeli halka üzerinde ve özellikle herhangi bir alan üzerinde doğrusal bir cebirsel grup olarak: bu, E'nin sözde bölünmüş (bazen "bükülmemiş" olarak da bilinir) ek biçimini tanımlar.7. Cebirsel olarak kapalı bir alan üzerinde, bu ve onun çift örtüsü tek biçimdir; bununla birlikte, diğer alanlara göre, genellikle E'nin birçok başka biçimi veya "kıvrımı" vardır.7genel çerçevesinde sınıflandırılanlar Galois kohomolojisi (üzerinde mükemmel alan k) set tarafından H1(k, Aut (E7)) hangi, çünkü E'nin Dynkin diyagramı7 (görmek altında ) otomorfizması yoktur, çakışır H1(k, E7, reklam).[1]
Reel sayılar alanında, bu cebirsel olarak bükülmüş E biçimlerinin kimliğinin gerçek bileşeni7 bahsedilen üç gerçek Lie grubu ile çakışıyor yukarıda, ancak temel grupla ilgili bir incelikle: E'nin tüm birleşik formları7 temel gruba sahip olmak Z/2Z cebirsel geometri anlamında, yani tam olarak bir çift kapak kabul ettikleri anlamına gelir; E'nin diğer kompakt olmayan gerçek Lie grubu formları7 bu nedenle cebirsel değildir ve hiçbir aslına sadık sonlu boyutlu temsilleri kabul etmez.
Sonlu alanlar üzerinde Lang-Steinberg teoremi ima ediyor ki H1(k, E7) = 0, yani E7 bükülmüş biçimleri yoktur: bkz. altında.
Cebir
Dynkin diyagramı
Dynkin diyagramı E için7 tarafından verilir ![]() .
.
Kök sistem

Coxeter – Dynkin diyagramı:
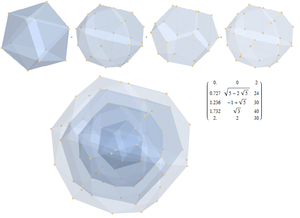
u = (1, φ, 0, -1, φ, 0,0)
v = (φ, 0, 1, φ, 0, -1,0)
w = (0, 1, φ, 0, -1, φ,0)
Öngörülen 231 politop Köşeler, her bir ölçülen norm setinin giderek şeffaflaşan gövdelerini oluşturan 3B normlarına göre sıralanır ve sıralanır. Bunlar şunları gösterir:
1) başlangıç noktasında 2 nokta
2) 2 ikosahedron
3) 1 icosadodecahedron
4) 2 on iki yüzlü
5) 1 icosadodecahedron
toplam 126 köşe için.
Kökler 7 boyutlu bir alana yayılsa da, onları 8 boyutlu bir vektör uzayının 7 boyutlu bir alt uzayında yatan vektörler olarak göstermek daha simetrik ve daha uygundur.
Kökler (1, −1,0,0,0,0,0,0) 'ın tüm 8 × 7 permütasyonları ve (ations, ½, ½, ½, −½, −½, −½, −½) permütasyonları
7 boyutlu alt uzayın, sekiz koordinatın toplamının sıfır olduğu alt uzay olduğuna dikkat edin. 126 kök var.
basit kökler vardır
- (0,−1,1,0,0,0,0,0)
- (0,0,−1,1,0,0,0,0)
- (0,0,0,−1,1,0,0,0)
- (0,0,0,0,−1,1,0,0)
- (0,0,0,0,0,−1,1,0)
- (0,0,0,0,0,0,−1,1)
- (½,½,½,½,−½,−½,−½,−½)
Bunlar, ilgili düğümleri Dynkin diyagramı yan düğüm en son olacak şekilde soldan sağa (yukarıda gösterilen diyagramda) sıralanır.
Alternatif bir açıklama
Kök sistemin alternatif (7 boyutlu) açıklaması, dikkate alınmasında yararlıdır. E7 × SU (2) olarak alt grubu E8, takip ediliyor:
Herşey son girişte sıfırı koruyan (± 1, ± 1,0,0,0,0,0) permütasyonları, takip eden tüm kökler çift sayıda + number
ve aşağıdaki iki kök
Böylece jeneratörler 66 boyutlu yani(12) alt cebir ve iki öz-eşlenik olarak dönüşen 64 jeneratör Weyl spinors nın-nin çevirmek(12) zıt kiralite ve kiralite üreteci ve diğer iki kiralite üreteci .
E göz önüne alındığında7 Cartan matrisi (aşağıda) ve a Dynkin diyagramı düğüm sıralaması: ![]()
- bir seçim basit kökler aşağıdaki matrisin satırları ile verilir:
Weyl grubu
Weyl grubu E7 2903040 mertebesindedir: 2. dereceden döngüsel grubun doğrudan ürünü ve benzersiz basit grup 1451520 siparişinin (PSp olarak tanımlanabilir)6(2) veya PSΩ7(2)).[2]
Cartan matrisi

Önemli alt hesaplar ve temsiller
E7 bir SU (8) alt cebirine sahiptir, çünkü kök sistemin 8 boyutlu tanımında, ilk kök grubu SU (8) kökleriyle özdeştir (aynı Cartan alt cebiri E'deki gibi7).
133 boyutlu birleşik gösterime ek olarak, bir 56 boyutlu "vektör" gösterimi, E'de bulunur8 birleşik temsil.
Gerçek ve karmaşık Lie cebirlerinin ve Lie gruplarının sonlu boyutlu temsillerinin karakterlerinin tümü, Weyl karakter formülü. En küçük indirgenemez temsillerin boyutları (dizi A121736 içinde OEIS ):
- 1, 56, 133, 912, 1463, 1539, 6480, 7371, 8645, 24320, 27664, 40755, 51072, 86184, 150822, 152152, 238602, 253935, 293930, 320112, 362880, 365750, 573440, 617253, 861840, 885248, 915705, 980343, 2273920, 2282280, 2785552, 3424256, 3635840...
Yukarıdaki dizideki altı çizili terimler, E'nin ek formunun sahip olduğu indirgenemez temsillerin boyutlarıdır.7 (eşdeğer olarak, ağırlıkları E'nin kök kafesine ait olanlar7), halbuki tam dizi, basitçe bağlantılı E formunun indirgenemez temsillerinin boyutlarını verir.7. 1903725824, 16349520330, vb. Boyutların izomorfik olmayan indirgenemez temsili vardır.
temel temsiller 133, 8645, 365750, 27664, 1539, 56 ve 912 boyutlarına sahip olanlar (içindeki yedi düğüme karşılık gelir) Dynkin diyagramı için seçilen sırayla Cartan matrisi yukarıda, yani düğümler ilk olarak altı düğümlü zincirde okunur, son düğüm üçüncü ile bağlanır).
E7 Polinom Değişkenleri
E7 56 değişmeli olmayan değişkende aşağıdaki polinom çiftinin otomorfizm grubudur. Değişkenleri 28'lik iki gruba ayırıyoruz, (p, P) ve (q, Q) nerede p ve q gerçek değişkenlerdir ve P ve Q 3 × 3 sekizlik Hermit matrisleri. O halde ilk değişmez, Sp'in semplektik değişmezidir (56, R):
İkinci daha karmaşık değişmez, bir simetrik kuartik polinom:
Nerede ve ikili daire operatörü şu şekilde tanımlanır: .
Cartan tarafından oluşturulan alternatif bir kuartik polinom değişmezi, her biri 28 bileşen içeren iki anti-simetrik 8x8 matris kullanır.
E tipi Chevalley grupları7
A üzerindeki noktalar sonlu alan ile q (bölünmüş) cebirsel E grubunun elemanları7 (görmek yukarıda ), ister ek (merkezsiz) ister basitçe bağlantılı form (cebirsel evrensel örtüsü) olsun, sonlu bir Chevalley grubu. Bu, E yazılan grupla yakından bağlantılı7(q), ancak bu gösterimde birkaç şeye karşılık gelebilecek belirsizlik vardır:
- üzerindeki noktalardan oluşan sonlu grup Fq basitçe bağlantılı E biçiminin7 (netlik için bu yazılabilir E7, sık iğne(q) ve E tipi "evrensel" Chevalley grubu olarak bilinir7 bitmiş Fq),
- (nadiren) üzerindeki noktalardan oluşan sonlu grup Fq E'nin ek formunun7 (netlik için bu yazılabilir E7, reklam(q) ve E tipi "ek" Chevalley grubu olarak bilinir.7 bitmiş Fq) veya
- birinciden ikincisine doğal haritanın görüntüsü olan sonlu grup: bu, E ile gösterilecek olan şeydir.7(q) aşağıda, sonlu gruplarla ilgili metinlerde en yaygın olduğu gibi.
Sonlu grup perspektifinden, bu üç grup arasındaki ilişki, SL arasındakine oldukça benzer (n, q), PGL (n, q) ve PSL (n, q), şu şekilde özetlenebilir: E7(q) herhangi biri için basittir q, E7, sık iğne(q) onun Schur kapağı ve E7, reklam(q) otomorfizm grubunda yer alır; dahası, ne zaman q 2'nin gücüdür, üçü de çakışır, aksi halde (ne zaman q garip), E'nin Schur çarpanı7(q) 2 ve E7(q) E dizininde 2 dizinindedir7, reklam(q), bu da neden E7, sık iğne(q) ve E7, reklam(q) genellikle 2 · E olarak yazılır7(q) ve E7(q) · 2. Cebirsel grup perspektifinden, E için daha az yaygındır7(q) sonlu basit gruba atıfta bulunmak için, çünkü ikincisi doğal bir şekilde bir cebirsel grubun noktaları kümesi değildir. Fq E'nin aksine7, sık iğne(q) ve E7, reklam(q).
Yukarıda belirtildiği gibi, E7(q) herhangi biri için basittir q,[3][4] ve tarafından hitap edilen sonsuz ailelerden birini oluşturur. sonlu basit grupların sınıflandırılması. Eleman sayısı formülle verilir (dizi A008870 içinde OEIS ):
E sırası7, sık iğne(q) veya E7, reklam(q) (her ikisi de eşittir) bölme faktörü gcd (2, q−1) (sıra A008869 içinde OEIS ). E'nin Schur çarpanı7(q) gcd (2, q−1) ve dış otomorfizm grubu, diyagonal otomorfizm grubunun ürünüdür Z/ gcd (2, q−1)Z (E eylemi ile verilir7, reklam(q)) ve alan otomorfizmleri grubu (yani düzen döngüsü f Eğer q = pf nerede p asaldır).
Fizikteki önemi
N = 8 süper yerçekimi dört boyutta boyutsal indirgeme 11 boyutlu süper yerçekiminden bir E kabul edin7 bosonic global simetri ve bir SU (8) bosonic yerel simetri. Fermiyonlar SU (8) temsillerindedir, gösterge alanları E temsilindedir.7ve skalarlar her ikisinin bir temsilindedir (Gravitonlar atletler her ikisine göre). Fiziksel durumlar kosetin temsillerindedir E7 / SU (8).
İçinde sicim teorisi, E7 bir parçası olarak görünür gösterge grubu biri (kararsız vesüpersimetrik ) sürümleri heterotik dizi. Kırılmamış gösterge grubunda da görünebilir E8 × E7 heterotik sicim teorisinin altı boyutlu kompaktlaştırmalarında, örneğin dört boyutlu yüzeyde K3.
Ayrıca bakınız
Notlar
- ^ Platonov, Vladimir; Rapinchuk Andrei (1994) [1991], Cebirsel gruplar ve sayı teorisi, Saf ve Uygulamalı Matematik, 139, Boston, MA: Akademik Basın, ISBN 978-0-12-558180-6, BAY 1278263 (Orijinal versiyon: Платонов, Владимир П .; Рапинчук, Андрей С. (1991). Алгебраические группы ve теория чисел. Наука. ISBN 5-02-014191-7.), §2.2.4
- ^ Conway, John Horton; Curtis, Robert Turner; Norton, Simon Phillips; Parker, Richard A; Wilson, Robert Arnott (1985). Sonlu Gruplar Atlası: Basit Gruplar için Maksimum Alt Gruplar ve Sıradan Karakterler. Oxford University Press. s. 46. ISBN 0-19-853199-0.
- ^ Carter, Roger W. (1989). Yalan Tipinin Basit Grupları. Wiley Classics Kitaplığı. John Wiley & Sons. ISBN 0-471-50683-4.
- ^ Wilson, Robert A. (2009). Sonlu Basit Gruplar. Matematikte Lisansüstü Metinler. 251. Springer-Verlag. ISBN 1-84800-987-9.
Referanslar
- Adams, J. Frank (1996), İstisnai Lie grupları üzerine dersler, Chicago Matematik Dersleri, Chicago Press Üniversitesi, ISBN 978-0-226-00526-3, BAY 1428422
- John Baez, Oktonyonlar, Bölüm 4.5: E7, Boğa. Amer. Matematik. Soc. 39 (2002), 145-205. Adresinde çevrimiçi HTML sürümü http://math.ucr.edu/home/baez/octonions/node18.html.
- E. Cremmer ve B. Julia, N = 8 Süper yerçekimi Teorisi. 1. Lagrangian, Phys.Lett.B80: 48,1978. Çevrimiçi taranmış sürüm http://ac.els-cdn.com/0370269378903039/1-s2.0-0370269378903039-main.pdf?_tid=79273f80-539d-11e4-a133-00000aab0f6c&acdnat=1413289833_5f3539a6365149b1064ddcec88.








![C_ {1} = pq-qp + Tr [PQ] -Tr [QP]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7710b7d259b59a9a6a8d8b18fcd632af7054eb6)
![C_ {2} = (pq + Tr [P circ Q]) ^ {2} + pTr [Q circ { tilde {Q}}] + qTr [P circ { tilde {P}}] + Tr [{ tilde {P}} circ { tilde {Q}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8e3fd1152c0065a4edbd173f1ddaf8b25964bd4)


![C_ {2} = Tr [(XY) ^ {2}] - { dfrac {1} {4}} Tr [XY] ^ {2} + { frac {1} {96}} epsilon _ {{ ijklmnop}} left (X ^ {{ij}} X ^ {{kl}} X ^ {{mn}} X ^ {{op}} + Y ^ {{ij}} Y ^ {{kl}} Y ^ {{mn}} Y ^ {{op}} sağ)](https://wikimedia.org/api/rest_v1/media/math/render/svg/6282baf57eda5d68498c5eb85830709fa9484ee9)

