Coxeter – Dynkin diyagramı - Coxeter–Dynkin diagram

Temel sonlu Coxeter grupları için Coxeter-Dynkin diyagramları

Temel afin Coxeter grupları için Coxeter-Dynkin diyagramları

İçinde geometri, bir Coxeter – Dynkin diyagramı (veya Coxeter diyagramı, Coxeter grafiği) bir grafik sayısal olarak etiketlenmiş kenarları olan ( şubeler) bir koleksiyon arasındaki mekansal ilişkileri temsil eden aynalar (veya yansıtan hiper düzlemler ). Bir sürekli değişen yapı: her bir grafik "düğüm" bir aynayı (etki alanı faset ) ve bir dala iliştirilmiş etiket, Dihedral açı iki ayna arasında sıralama (bir etki alanında çıkıntı ), yani yansıtıcı düzlemler arasındaki açının 180 derece elde etmek için çarpılabileceği miktar. Etiketlenmemiş bir dal, dolaylı olarak sıra-3'ü (60 derece) temsil eder.

Her diyagram bir Coxeter grubu ve Coxeter grupları, ilişkili diyagramlarına göre sınıflandırılır.

Dynkin diyagramları Coxeter diyagramlarından iki açıdan farklılık gösteren yakından ilişkili nesnelerdir: birincisi, "4" veya daha büyük etiketli dallar yönetilen Coxeter diyagramları yönsüz; ikinci olarak, Dynkin diyagramları ek bir (kristalografik ) kısıtlama, yani izin verilen tek dal etiketleri 2, 3, 4 ve 6'dır. Dynkin diyagramları, sınıflandırmaya karşılık gelir ve bunları sınıflandırmak için kullanılır. kök sistemler ve bu nedenle yarıbasit Lie cebirleri.^[1]

Açıklama

Bir Coxeter – Dynkin diyagramının dalları bir rasyonel sayı p, temsil eden Dihedral açı 180 ° /p. Ne zaman $p = 2$ açı 90 ° 'dir ve aynaların etkileşimi yoktur, bu nedenle dal diyagramdan çıkarılabilir. Bir dal etiketlenmemişse, sahip olduğu varsayılır $p = 3$ , 60 ° 'lik bir açıyı temsil eder. İki paralel aynanın "∞" ile işaretlenmiş bir dalı vardır. Prensipte, n aynalar bir ile temsil edilebilir tam grafik hepsinin içinde n( $n - 1) / 2$ dallar çizilir. Pratikte, aynaların neredeyse tüm ilginç konfigürasyonları bir dizi dik açı içerir, bu nedenle karşılık gelen dallar çıkarılır.

Diyagramlar, grafik yapılarına göre etiketlenebilir. Tarafından incelenen ilk formlar Ludwig Schläfli bunlar ortoşemler doğrusal grafiklere sahip olan normal politoplar ve normal petekler. Plagioschemes vardır basitler dallanma grafikleriyle temsil edilir ve siklosşemler döngüsel grafiklerle temsil edilen basitliklerdir.

Schläfli matrisi

Her Coxeter diyagramına karşılık gelen Schläfli matrisi (adını Ludwig Schläfli ), matris öğeleriyle $a ben, j = a j, ben = -2cos (π / p)$ nerede p ayna çiftleri arasındaki dal sırasıdır. Olarak kosinüs matrisi, aynı zamanda a Gram matrisi sonra Jørgen Pedersen Gram. Herşey Coxeter grubu Schläfli matrisleri simetriktir çünkü kök vektörleri normalize edilmiştir. İle yakından ilgilidir Cartan matrisi, benzer ancak yönlendirilmiş grafikte kullanılır Dynkin diyagramları p = 2,3,4 ve 6 gibi sınırlı durumlarda genel olarak simetrik DEĞİLDİR.

Schläfli matrisinin determinantı olarak adlandırılan Schläflianve işareti, grubun sonlu (pozitif), afin (sıfır), belirsiz (negatif) olup olmadığını belirler. Bu kurala denir Schläfli Kriteri.^[2]

özdeğerler Schläfli matrisinin, bir Coxeter grubunun olup olmadığını belirler. sonlu tip (hepsi olumlu), afin tipi (tümü negatif olmayan, en az biri sıfırdır) veya belirsiz tip (aksi takdirde). Belirsiz tip bazen daha da alt bölümlere ayrılır, ör. hiperbolik ve diğer Coxeter gruplarına. Bununla birlikte, hiperbolik Coxeter grupları için eşdeğer olmayan birden fazla tanım vardır. Aşağıdaki tanımı kullanıyoruz: Bağlı diyagramı olan bir Coxeter grubu hiperbolik ne sonlu ne de afin tipte ise, ancak her uygun bağlantılı alt diyagram sonlu veya afin tipteyse. Hiperbolik bir Coxeter grubu kompakt tüm alt gruplar sonlu ise (yani pozitif belirleyicilere sahipse) ve parakompakt tüm alt grupları sonlu veya afin ise (yani, negatif olmayan belirleyicilere sahipse).

Sonlu ve afin gruplar da denir eliptik ve parabolik sırasıyla. Hiperbolik gruplar, 1950'de kompakt hiperbolik grupları sıralayan F.Lannér'den sonra Lannér olarak da adlandırılır.^[3] ve parakompakt gruplar için Koszul (veya yarı-Lannér).

Rank 2 Coxeter grupları

Sıra 2 için, bir Coxeter grubunun türü, yalnızca özdeğerlerin ürünü olduğundan, Schläfli matrisinin determinantı tarafından tamamen belirlenir: Sonlu tip (pozitif belirleyici), afin tipi (sıfır belirleyici) veya hiperbolik (negatif belirleyici) . Coxeter bir eşdeğeri kullanır parantez notasyonu düğüm-dal grafik diyagramlarının bir ikamesi olarak dal sıraları dizilerini listeler. Akılcı çözümler [p / q], ayrıca var gcd (p, q) = 1, örtüşen temel alanları tanımlar. Örneğin 3/2, 4/3, 5/2, 5/3, 5/4. ve 6/5.

Tür	Sonlu					Afin	Hiperbolik
Geometri					...
Coxeter	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ / λ]
Sipariş	2	4	6	8	2p	∞
Ayna çizgileri, Coxeter diyagram düğümlerine karşılık gelecek şekilde renklendirilmiştir. Temel alanlar dönüşümlü olarak renklendirilmiştir.

Rank 2 Coxeter grup diyagramları
Sipariş p	Grup	Coxeter diyagramı		Schläfli matrisi
Sipariş p	Grup	Coxeter diyagramı		${displaystyle left [{egin {matrix} 2 & a_ {12} a_ {21} & 2end {matrix}} ight]}$	Belirleyici (4-bir₂₁* a₁₂)
Sonlu (Belirleyici> 0)
2	ben₂(2) = A₁xA₁		[2]	${displaystyle left [{egin {smallmatrix} 2 & 0 0 & 2end {smallmatrix}} ight]}$	4
3	ben₂(3) = bir₂		[3]	${displaystyle sol [{egin {smallmatrix} 2 & -1 -1 & 2end {smallmatrix}} ight]}$	3
3/2			[3/2]	${displaystyle left [{egin {smallmatrix} 2 & 1 1 & 2end {smallmatrix}} ight]}$	3
4	ben₂(4) = B₂		[4]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2}} - {sqrt {2}} & 2end {smallmatrix}} ight]}$	2
4/3			[4/3]	${displaystyle left [{egin {smallmatrix} 2 & {sqrt {2}} {sqrt {2}} & 2end {smallmatrix}} ight]}$	2
5	ben₂(5) = H₂		[5]	${displaystyle sol [{egin {smallmatrix} 2 & -phi -phi & 2end {smallmatrix}} ight]}$	${displaystyle (5- {sqrt {5}}) / 2}$ ~1.38196601125
5/4			[5/4]	${displaystyle sol [{egin {smallmatrix} 2 & phi phi & 2end {smallmatrix}} ight]}$	${displaystyle (5- {sqrt {5}}) / 2}$ ~1.38196601125
5/2			[5/2]	${displaystyle sol [{egin {smallmatrix} 2 & 1-phi 1-phi & 2end {smallmatrix}} ight]}$	${displaystyle (5+ {sqrt {5}}) / 2}$ ~3.61803398875
5/3			[5/3]	${displaystyle sol [{egin {smallmatrix} 2 & phi -1 phi -1 & 2end {smallmatrix}} ight]}$	${displaystyle (5+ {sqrt {5}}) / 2}$ ~3.61803398875
6	ben₂(6) = G₂		[6]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {3}} - {sqrt {3}} & 2end {smallmatrix}} ight]}$	1
6/5			[6/5]	${displaystyle left [{egin {smallmatrix} 2 & {sqrt {3}} {sqrt {3}} & 2end {smallmatrix}} ight]}$	1
8	ben₂(8)		[8]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2+ {sqrt {2}}}} - {sqrt {2+ {sqrt {2}}}} & 2end {smallmatrix}} ight]}$	${displaystyle 2- {sqrt {2}}}$ ~0.58578643763
10	ben₂(10)		[10]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {(5+ {sqrt {5}}) / 2}} - {sqrt {(5+ {sqrt {5}}) / 2}} & 2end {smallmatrix }} ight]}$	${displaystyle (3- {sqrt {5}}) / 2}$ ~0.38196601125
12	ben₂(12)		[12]	${displaystyle left [{egin {smallmatrix} 2 & - {sqrt {2+ {sqrt {3}}}} - {sqrt {2+ {sqrt {3}}}} & 2end {smallmatrix}} ight]}$	${displaystyle 2- {sqrt {3}}}$ ~0.26794919243
p	ben₂(p)		[p]	${displaystyle sol [{egin {smallmatrix} 2 & -2cos (pi / p) - 2cos (pi / p) & 2end {smallmatrix}} ight]}$	${displaystyle 4sin ^ {2} (pi / p)}$
Afin (Belirleyici = 0)
∞	ben₂(∞) = ${displaystyle {ilde {I}} _ {1}}$ = ${displaystyle {ilde {A}} _ {1}}$		[∞]	${displaystyle sol [{egin {smallmatrix} 2 & -2 -2 & 2end {smallmatrix}} ight]}$	0
Hiperbolik (Determinant≤0)
∞			[∞]	${displaystyle sol [{egin {smallmatrix} 2 & -2 -2 & 2end {smallmatrix}} ight]}$	0
∞			[iπ / λ]	${displaystyle sol [{egin {smallmatrix} 2 & -2cosh (2lambda) - 2cosh (2lambda) & 2end {smallmatrix}} ight]}$	${displaystyle -4sinh ^ {2} (2lambda) leq 0}$

Geometrik görselleştirmeler

Coxeter-Dynkin diyagramı, şunların grafik bir açıklaması olarak görülebilir. temel alan aynaların. Bir ayna bir hiper düzlem belirli bir boyutlu küresel veya Öklid veya hiperbolik uzay içinde. (2B alanlarda ayna bir çizgidir ve 3B'de ayna bir düzlemdir).

Bu görselleştirmeler, 2B ve 3B Öklid grupları ve 2B küresel gruplar için temel alanları gösterir. Her biri için Coxeter diyagramı, hiper düzlem aynaları tanımlanarak ve 90 derecelik dihedral açıları göz ardı ederek bağlantılarını etiketleyerek çıkarılabilir (sıra 2).

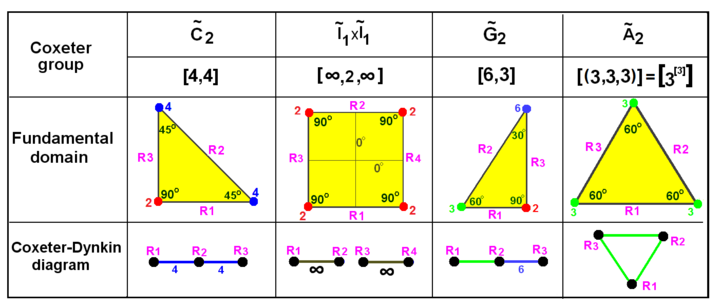Eşdeğer diyagramlarla Öklid düzleminde Coxeter grupları. Yansımalar grafik düğümleri olarak etiketlenir R1, R2, vb. Ve yansıtma sıralarına göre renklendirilir. 90 derecedeki yansımalar etkisizdir ve bu nedenle diyagramdan gizlenir. Paralel aynalar, ∞ etiketli bir dal ile bağlanır. Prizmatik grup ${displaystyle {ilde {I}} _ {1}}$ x ${displaystyle {ilde {I}} _ {1}}$ ikiye katlanarak gösterilir ${displaystyle {ilde {C}} _ {2}}$ , ancak aynı zamanda iki katına çıkarılarak dikdörtgen alanlar olarak da oluşturulabilir. ${displaystyle {ilde {G}} _ {2}}$ üçgenler. ${displaystyle {ilde {A}} _ {2}}$ ikiye katlamak ${displaystyle {ilde {G}} _ {2}}$ üçgen.
Birçok Coxeter grubu hiperbolik düzlem Öklid vakalarından bir dizi hiperbolik çözüm olarak genişletilebilir.
Diyagramlı 3-uzayda Coxeter grupları. Aynalar (üçgen yüzler) ters köşe 0..3 ile etiketlenir. Dallar yansıma sırasına göre renklendirilir. ${displaystyle {ilde {C}} _ {3}}$ küpün 1 / 48'ini doldurur. ${displaystyle {ilde {B}} _ {3}}$ küpün 1 / 24'ünü doldurur. ${displaystyle {ilde {A}} _ {3}}$ küpün 1 / 12'sini doldurur.	Eşdeğer diyagramlarla küredeki Coxeter grupları. Bir temel alan sarı ile özetlenmiştir. Etki alanı köşeleri (ve grafik dalları) yansıma sıralarına göre renklendirilir.

Sonlu Coxeter grupları

Ayrıca bakınız politop aileleri bu gruplarla ilişkili bir uç düğüm tek tip politop tablosu için.

Aynı gruplar için üç farklı sembol verilir - harf / sayı olarak, parantez içine alınmış sayılar dizisi ve Coxeter diyagramı olarak.
Çatallı D_n gruplar yarım veya dönüşümlü normal C versiyonu_n gruplar.
Çatallı D_n ve E_n gruplar ayrıca bir üst simge form [3^a,b,c] nerede a,b,c üç dalın her birindeki bölümlerin sayısıdır.

Bağlı sonlu Coxeter-Dynkin diyagramları (1'den 9'a kadar sıralar)
Sıra	Basit Lie grupları			Olağanüstü Lie grupları
Sıra	${displaystyle {A} _ {1+}}$	${displaystyle {B} _ {2+}}$	${displaystyle {D} _ {2+}}$	${displaystyle {E} _ {3-8}}$	${displaystyle {F} _ {3-4}}$	${displaystyle {G} _ {2}}$	${displaystyle {H} _ {2-4}}$	${displaystyle {I} _ {2} (p)}$
1	Bir₁=[ ]
2	Bir₂=[3]	B₂=[4]	D₂= A₁Bir₁			G₂=[6]	H₂=[5]	ben₂[p]
3	Bir₃=[3²]	B₃=[3,4]	D₃= A₃	E₃= A₂Bir₁	F₃= B₃		H₃
4	Bir₄=[3³]	B₄=[3²,4]	D₄=[3^1,1,1]	E₄= A₄	F₄		H₄
5	Bir₅=[3⁴]	B₅=[3³,4]	D₅=[3^2,1,1]	E₅= D₅
6	Bir₆=[3⁵]	B₆=[3⁴,4]	D₆=[3^3,1,1]	E₆=[3^2,2,1]
7	Bir₇=[3⁶]	B₇=[3⁵,4]	D₇=[3^4,1,1]	E₇=[3^3,2,1]
8	Bir₈=[3⁷]	B₈=[3⁶,4]	D₈=[3^5,1,1]	E₈=[3^4,2,1]
9	Bir₉=[3⁸]	B₉=[3⁷,4]	D₉=[3^6,1,1]
10+	..	..	..	..

Tek tip politoplarla uygulama

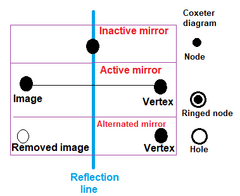Tek tip politoplar oluştururken düğümler şu şekilde işaretlenir: aktif Bir jeneratör noktası aynanın dışındaysa, bir jeneratör noktası ile ayna görüntüsü arasında yeni bir kenar oluşturarak bir halka ile. Halkasız bir düğüm bir inaktif yeni nokta üretmeyen ayna. Düğümü olmayan bir halka a delik.	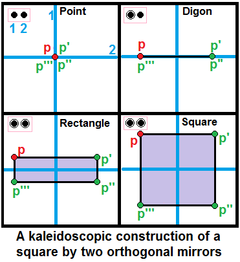Bir kare oluşturmak için iki ortogonal ayna kullanılabilir, burada kırmızı bir jeneratör noktası ve aynaların karşısında 3 sanal kopya ile görülüyor. Bir iç mekan oluşturmak için bu ortogonal durumda jeneratörün her iki aynanın da kapalı olması gerekir. Halka işaretlemesi, aktif halkaların tüm aynalardan eşit uzaklıkta jeneratörlere sahip olduğunu varsayarken, dikdörtgen aynı zamanda tek tip olmayan bir çözümü de temsil edebilir.

Coxeter-Dynkin diyagramları, neredeyse tüm sınıfları açık bir şekilde numaralandırabilir. tek tip politop ve tek tip mozaikler. Saf yansıtıcı simetriye sahip her tek tip politop (birkaç özel durum dışında tümü saf yansıma simetrisine sahiptir), permütasyonlu bir Coxeter-Dynkin diyagramı ile temsil edilebilir. işaretlemeler. Her bir tek tip politop, bu tür aynalar ve tek bir jeneratör noktası kullanılarak oluşturulabilir: ayna görüntüleri, yansımalar olarak yeni noktalar oluşturur, ardından politop kenarlar noktalar ve bir ayna görüntüsü noktası arasında tanımlanabilir. Yüzler sonunda orijinal oluşturucuya sarılan bir kenarın tekrarlanan yansıması ile üretilir; son şekil ve herhangi bir yüksek boyutlu yüzey benzer şekilde bir alanı çevrelemek için yansıtılan yüz tarafından yaratılır.

Oluşturan tepe noktasını belirlemek için, bir veya daha fazla düğüm halkalarla işaretlenir, yani tepe değil halkalı düğüm (ler) ile temsil edilen ayna (lar) üzerinde. (İki veya daha fazla ayna işaretlenmişse, tepe onlardan eşit uzaklıktadır.) Bir ayna aktif (yansımalar yaratır) sadece üzerinde olmayan noktalara göre. Bir diyagramın bir politopu temsil etmesi için en az bir aktif düğüme ihtiyacı vardır. Bağlantısız bir diyagram (sıra 2 dallarıyla ayrılmış alt gruplar veya ortogonal aynalar) her alt grafikte en az bir etkin düğüm gerektirir.

Herşey normal politoplar, ile temsil edilen Schläfli sembolü { $p, q, r, ...$ }, sahip olabilir temel alanlar bir dizi ile temsil edilir n ile etiketlenmiş bir düğüm ve dal hattının ilgili Coxeter – Dynkin diyagramı ile aynalar $p, q, r, ...,$ ilk düğüm halkalı.

Tek halkalı tek biçimli politoplar, temel alan simpleksinin köşelerindeki üretici noktalarına karşılık gelir. İki halka, simpleksin kenarlarına karşılık gelir ve eşit kenar uzunlukları için tek tip çözüm olarak sadece orta nokta ile bir serbestlik derecesine sahiptir. Genel olarak khalka jeneratör noktaları açık (k-1)- simpleksin yüzleri ve tüm düğümler halkalıysa, jeneratör noktası simpleksin içindedir.

Yansımasız simetriye sahip tek tip politopların özel durumu, halkalı bir düğümün merkezi noktasının kaldırıldığı ikincil bir işaret ile temsil edilir ( delik). Bu şekiller dönüşümler^{[açıklama gerekli ]} yansıtıcı simetriye sahip politopların, alternatif düğümlerin silindiğini ima eder^{[açıklama gerekli ]}. Ortaya çıkan politop, orijinalin bir alt simetrisine sahip olacaktır. Coxeter grubu. Kesilmiş bir alternatife denir küçümsemek.

Tek bir düğüm, tek bir aynayı temsil eder. Buna A grubu denir₁. Halkalıysa bu bir çizgi segmenti aynaya dik, {} ile temsil edilir.
İki bağlı olmayan düğüm ikisini temsil eder dik aynalar. Her iki düğüm de halkalıysa, bir dikdörtgen oluşturulabilir veya bir Meydan nokta her iki aynadan eşit uzaklıkta ise.
Bir siparişle bağlanan iki düğümn şube bir n-gen nokta bir aynadaysa ve 2nnokta her iki aynadan uzaksa -gen. Bu I oluşturur₁(n) grubu.
İki paralel ayna sonsuz bir çokgeni temsil edebilir I₁(∞) grubu, Ĩ olarak da adlandırılır₁.
Üçgen şeklindeki üç ayna, geleneksel olarak görülen görüntüler kaleydoskop ve bir üçgene bağlı üç düğümle temsil edilebilir. Yinelenen örneklerde (3 3 3), (2 4 4), (2 3 6) olarak etiketlenmiş dallar olacaktır, ancak son ikisi bir çizgi olarak çizilebilir ( 2 dallar görmezden gelinir). Bunlar üretecek tek tip döşemeler.
Üç ayna üretebilir tekdüze çokyüzlü; rasyonel sayılar dahil olmak üzere kümesini verir Schwarz üçgenleri.
Biri diğer ikisine dik olan üç ayna, tek tip prizmalar.

Temel etki alanı içindeki 7 topolojik jeneratör konumuna dayanan genel bir üçgen içinde 7 yansıtıcı tek tip yapı vardır. Her aktif ayna bir kenar oluşturur, iki aktif aynanın alan taraflarında jeneratörleri ve iç kısımda üç aktif aynanın jeneratörü vardır. Ortaya çıkan çok yüzlü veya döşemenin eşit kenar uzunlukları için benzersiz bir konum için bir veya iki serbestlik derecesi çözülebilir.	Örnek 7 jeneratörler sekiz yüzlü simetri, temel alan üçgeni (4 3 2), bir dönüşüm

Düzgün politopların ikili kısımları bazen halkalı düğümlerin yerini alan dikey bir eğik çizgi ve çıkıntıların delik düğümleri için bir eğik çizgi ile işaretlenir. Örneğin, temsil eder dikdörtgen (iki aktif ortogonal ayna olarak) ve temsil eder çift çokgen, eşkenar dörtgen.

Örnek çokyüzlüler ve döşemeler

Örneğin, B₃ Coxeter grubu bir diyagrama sahiptir: . Bu aynı zamanda sekiz yüzlü simetri.

7 dışbükey var tekdüze çokyüzlü bu simetri grubundan ve 3'ünden de oluşturulabilir. dönüşüm her biri benzersiz bir şekilde işaretlenmiş Coxeter – Dynkin diyagramına sahip alt simetriler. Wythoff sembolü 3. sıra grafikleri için Coxeter diyagramının özel bir durumunu temsil eder ve 2 dal sırasını gizlemek yerine 3 dal sırasının tümü adlandırılır. Wythoff sembolü, küçümsemek form, ancak tüm düğümler halkasız genel değişimler değil.

Düzgün oktahedral çokyüzlüler
Simetri: [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t {4,3}	r {4,3} r {3^1,1}	t {3,4} t {3^1,1}	{3,4} {3^1,1}	rr {4,3} s₂{3,4}	tr {4,3}	sr {4,3}	s {4,3} {3,3}	h₂{4,3} t {3,3}	s {3,4} s {3^1,1}

		=	=	=				= veya	= veya	=

Tekdüze çokyüzlülere çiftler
V4³	V3.8²	V (3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Aynı yapılar, üniforma gibi ayrık (ortogonal) Coxeter grupları üzerinde yapılabilir. prizmalar ve daha net bir şekilde dihedronlar ve hosohedronlar kürede, bunun gibi [6] × [] veya [6,2] aile:

Düzgün altıgen dihedral küresel çokyüzlüler
Simetri: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t {6,2}	r {6,2}	t {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	s {2,6}
Üniformalı çiftler

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Buna karşılık, [6,3], familyası, Öklid düzleminin 7 tek tip eğiminden oluşan paralel bir set ve bunların ikili eğimlerini üretir. Yine 3 alternatif ve bazı yarı simetri versiyonu vardır.

Düzgün altıgen / üçgen eğimler [ v t e ]
Simetri: [6,3], (*632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t {6,3}	r {6,3}	t {3,6}	{3,6}	rr {6,3}	tr {6,3}	sr {6,3}	s {3,6}


6³	3.12²	(3.6)²	6.6.6	3⁶	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Üniforma ikilileri

V6³	V3.12²	V (3.6)²	V6³	V3⁶	V3.4.6.4	V.4.6.12	V3⁴.6	V3⁶

Hiperbolik düzlemde [7,3], familyası, paralel bir tek tip döşeme seti ve bunların ikili döşemelerini üretir. Sadece 1 alternatif var (küçümsemek ) çünkü tüm şube siparişleri tuhaftır. Tek tip döşemelerin diğer birçok hiperbolik ailesi de görülebilir. hiperbolik düzlemde tek tip eğimler.

Düzgün altıgen / üçgen eğimler [ v t e ]
Simetri: [7,3], (*732)							[7,3]⁺, (732)


{7,3}	t {7,3}	r {7,3}	t {3,7}	{3,7}	rr {7,3}	tr {7,3}	sr {7,3}
Üniforma ikilileri


V7³	V3.14.14	V3.7.3.7	V6.6.7	V3⁷	V3.4.7.4	V4.6.14	V3.3.3.3.7

Affine Coxeter grupları

Dışbükey tek tip Öklid mozaiklerinin aileleri, afin Coxeter grupları. Bu gruplar, eklenen bir düğümün dahil edilmesiyle sonlu gruplarla aynıdır. Harf isimlerinde, harfin üzerinde "~" ile aynı harf verilir. Dizin, sonlu grubu ifade eder, dolayısıyla sıra, dizin artı 1'dir. (Ernst Witt afin gruplar için semboller şu şekilde verilmiştir: Ayrıca)

${displaystyle {ilde {A}} _ {n-1}}$ : bu türdeki diyagramlar döngüdür. (Ayrıca P_n)
${displaystyle {ilde {C}} _ {n-1}}$ ile ilişkili hiperküp düzenli mozaikleme { $4, 3, ...., 4$ } aile. (Ayrıca R_n)
${displaystyle {ilde {B}} _ {n-1}}$ kaldırılmış bir ayna ile C ile ilişkili. (Ayrıca S_n)
${displaystyle {ilde {D}} _ {n-1}}$ kaldırılmış iki aynayla C ile ilişkili. (Ayrıca Q_n)
${displaystyle {ilde {E}} _ {6}}$ , ${displaystyle {ilde {E}} _ {7}}$ , ${displaystyle {ilde {E}} _ {8}}$ . (Ayrıca T₇, T₈, T₉)
${displaystyle {ilde {F}} _ {4}}$ {3,4,3,3} düzenli mozaiklemeyi oluşturur. (Ayrıca U₅)
${displaystyle {ilde {G}} _ {2}}$ 30-60-90 üçgen temel alanlarını oluşturur. (Ayrıca V₃)
${displaystyle {ilde {I}} _ {1}}$ iki paralel aynadır. (= ${displaystyle {ilde {A}} _ {1}}$ = ${displaystyle {ilde {C}} _ {1}}$ ) (Ayrıca W₂)

Kompozit gruplar, ortogonal projeler olarak da tanımlanabilir. En yaygın kullanım ${displaystyle {ilde {A}} _ {1}}$ , sevmek ${displaystyle {ilde {A}} _ {1} ^ {2}}$ , kare veya dikdörtgeni temsil eder dama tahtası Öklid düzlemindeki alanlar. Ve ${displaystyle {ilde {A}} _ {1} {ilde {G}} _ {2}}$ temsil eder üçgen prizma Öklid 3-uzayında temel alanlar.

Affine Coxeter grafikleri (2 ila 10 düğüm)
Sıra	${displaystyle {ilde {A}} _ {1+}}$ (P₂₊)	${displaystyle {ilde {B}} _ {3+}}$ (S₄₊)	${displaystyle {ilde {C}} _ {1+}}$ (R₂₊)	${displaystyle {ilde {D}} _ {4+}}$ (Q₅₊)	${displaystyle {ilde {E}} _ {n}}$ (T_{n + 1}) / ${displaystyle {ilde {F}} _ {4}}$ (U₅) / ${displaystyle {ilde {G}} _ {2}}$ (V₃)
2	${displaystyle {ilde {A}} _ {1}}$ =[∞]		${displaystyle {ilde {C}} _ {1}}$ =[∞]
3	${displaystyle {ilde {A}} _ {2}}$ =[3^[3]] *		${displaystyle {ilde {C}} _ {2}}$ =[4,4] *		${displaystyle {ilde {G}} _ {2}}$ =[6,3] *
4	${displaystyle {ilde {A}} _ {3}}$ =[3^[4]] *	${displaystyle {ilde {B}} _ {3}}$ =[4,3^1,1] *	${displaystyle {ilde {C}} _ {3}}$ =[4,3,4] *	${displaystyle {ilde {D}} _ {3}}$ =[3^1,1,3⁻¹,3^1,1] = ${displaystyle {ilde {A}} _ {3}}$
5	${displaystyle {ilde {A}} _ {4}}$ =[3^[5]] *	${displaystyle {ilde {B}} _ {4}}$ =[4,3,3^1,1] *	${displaystyle {ilde {C}} _ {4}}$ =[4,3²,4] *	${displaystyle {ilde {D}} _ {4}}$ =[3^1,1,1,1] *	${displaystyle {ilde {F}} _ {4}}$ =[3,4,3,3] *
6	${displaystyle {ilde {A}} _ {5}}$ =[3^[6]] *	${displaystyle {ilde {B}} _ {5}}$ =[4,3²,3^1,1] *	${displaystyle {ilde {C}} _ {5}}$ =[4,3³,4] *	${displaystyle {ilde {D}} _ {5}}$ =[3^1,1,3,3^1,1] *
7	${displaystyle {ilde {A}} _ {6}}$ =[3^[7]] *	${displaystyle {ilde {B}} _ {6}}$ =[4,3³,3^1,1]	${displaystyle {ilde {C}} _ {6}}$ =[4,3⁴,4]	${displaystyle {ilde {D}} _ {6}}$ =[3^1,1,3²,3^1,1]	${displaystyle {ilde {E}} _ {6}}$ =[3^2,2,2]
8	${displaystyle {ilde {A}} _ {7}}$ =[3^[8]] *	${displaystyle {ilde {B}} _ {7}}$ =[4,3⁴,3^1,1] *	${displaystyle {ilde {C}} _ {7}}$ =[4,3⁵,4]	${displaystyle {ilde {D}} _ {7}}$ =[3^1,1,3³,3^1,1] *	${displaystyle {ilde {E}} _ {7}}$ =[3^3,3,1] *
9	${displaystyle {ilde {A}} _ {8}}$ =[3^[9]] *	${displaystyle {ilde {B}} _ {8}}$ =[4,3⁵,3^1,1]	${displaystyle {ilde {C}} _ {8}}$ =[4,3⁶,4]	${displaystyle {ilde {D}} _ {8}}$ =[3^1,1,3⁴,3^1,1]	${displaystyle {ilde {E}} _ {8}}$ =[3^5,2,1] *
10	${displaystyle {ilde {A}} _ {9}}$ =[3^[10]] *	${displaystyle {ilde {B}} _ {9}}$ =[4,3⁶,3^1,1]	${displaystyle {ilde {C}} _ {9}}$ =[4,3⁷,4]	${displaystyle {ilde {D}} _ {9}}$ =[3^1,1,3⁵,3^1,1]
11	...	...	...	...

Hiperbolik Coxeter grupları

Birçok sonsuz hiperbolik var Coxeter grupları. Hiperbolik gruplar, sınırlı temel alanlara sahip kompakt gruplar ile kompakt veya değil olarak kategorize edilir. Kompakt simpleks hiperbolik gruplar (Lannér basitleştiriyor) sıra 3 ila 5 olarak bulunur. Paracompact simpleks grupları (Koszul basitlikleri) 10. sıraya kadar mevcuttur. Hypercompact (Vinberg politopları) gruplar araştırılmış ancak tam olarak belirlenememiştir. 2006'da Allcock, 6'ya kadar boyutlar için sonsuz sayıda kompakt Vinberg politopu ve 19'a kadar boyut için sonsuz sayıda sonlu hacimli Vinberg politopu olduğunu kanıtladı.^[4] bu nedenle tam bir numaralandırma mümkün değildir. Hem basit hem de basit olmayan bu temel yansıtıcı alanların tümü, genellikle Coxeter politoplar veya bazen daha az doğru Coxeter çokyüzlü.

H'deki hiperbolik gruplar²

Poincaré disk modeli temel alanın üçgenler
Örnek dik üçgenler [p, q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Örnek genel üçgenler [(p, q, r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

İki boyutlu hiperbolik üçgen grupları aşağıdakiler için üçgen (p q r) ile tanımlanan sıra 3 Coxeter diyagramları olarak bulunur:

{displaystyle {frac {1} {p}} + {frac {1} {q}} + {frac {1} {r}} <1.}

Doğrusal ve üçgen grafikler dahil olmak üzere sonsuz sayıda kompakt üçgen hiperbolik Coxeter grubu vardır. Doğrusal grafikler, dik üçgenler için mevcuttur (r = 2 ile).^[5]

Kompakt hiperbolik Coxeter grupları

Doğrusal

Döngüsel

∞ [p, q],

:
2 (p + q)

...

...

...

∞ [(p, q, r)],

: p + q + r> 9

			...

Seviye 3'teki Paracompact Coxeter grupları, kompakt olanların sınırları olarak mevcuttur.

Doğrusal grafikler	Döngüsel grafikler
[p, ∞] [∞,∞]	[(p, q, ∞)] [(p, ∞, ∞)] [(∞,∞,∞)]

Aritmetik üçgen grubu

Hiperbolik üçgen grupları bunlar da aritmetik gruplar sonlu bir alt küme oluşturur. Bilgisayar aramasıyla tam liste belirlendi Kisao Takeuchi 1977 tarihli makalesinde Aritmetik üçgen grupları.^[6] Toplam 85, 76 kompakt ve 9 parakompakt vardır.

Dik üçgenler (p q 2)	Genel üçgenler (p q r)
Kompakt gruplar: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Paracompact dik üçgenler: (4) , , ,	Genel üçgenler: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Paracompact genel üçgenler: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Üçgenlerin üzerinde hiperbolik Coxeter poligonları

Dörtgen grupların temel alanları
İdeal köşelere sahip alanlar
veya [∞,3,∞] [iπ / λ₁, 3, iπ / λ₂] (*3222)	veya [((3,∞,3)),∞] [((3, iπ / λ₁, 3)), iπ / λ₂] (*3322)	veya [(3,∞)^[2]] [(3, iπ / λ₁, 3, iπ / λ₂)] (*3232)	veya [(4,∞)^[2]] [(4, iπ / λ₁, 4, iπ / λ₂)] (*4242)	(*3333)
[iπ / λ₁, ∞, iπ / λ₂] (*∞222)	(*∞∞22)	[(iπ / λ₁, ∞, iπ / λ₂,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Diğer H² hiperbolik kaleydoskoplar yüksek dereceli çokgenlerden oluşturulabilir. Sevmek üçgen grupları bu kaleydoskoplar, (a b c d ...) gibi temel alan etrafında ayna kesişim sıralarının döngüsel bir dizisi ile veya eşdeğer olarak tanımlanabilir. orbifold notasyonu gibi *abcd.... Bu poligonal kaleydoskoplar için Coxeter-Dynkin diyagramları dejenere (n-1) olarak görülebilir -basit dallar sırası a, b, c ... ve kalan n * (n-3) / 2 dalları ile temel alanlar, kesişmeyen aynaları temsil eden sonsuz (∞) olarak etiketlenir. Hiperbolik olmayan tek örnek, Öklid simetrisidir. Meydan veya dikdörtgen gibi , [∞, 2, ∞] (orbifold * 2222). Kesişmeyen aynalar için başka bir dal gösterimi Vinberg noktalı veya kesikli çizgiler olarak sonsuz dallar verir, bu nedenle bu diyagram şu şekilde gösterilebilir: , çevrenin etrafında bastırılmış dört 2. derece dal ile.

Örneğin, bir dörtgen alan (a b c d), ultra paralel aynaları birbirine bağlayan iki sonsuz sıralı dala sahip olacaktır. En küçük hiperbolik örnek , [∞, 3, ∞] veya [iπ / λ₁, 3, iπ / λ₂] (orbifold * 3222), burada (λ₁, λ₂) ultra paralel aynalar arasındaki mesafedir. Alternatif ifade şudur: , çevrenin etrafında bastırılmış üç sıra 2 dal ile. Benzer şekilde (2 3 2 3) (orbifold * 3232) şu şekilde temsil edilebilir: ve (3 3 3 3), (orbifold * 3333) tam bir grafik olarak gösterilebilir .

En yüksek dörtgen alan (∞ ∞ ∞ ∞), sonsuz bir karedir ve tam bir dört yüzlü için ideal köşeler olarak 4 çevre dalı ve sonsuz olarak iki diyagonal dalı olan grafik (noktalı çizgilerle gösterilmiştir) için ultra paralel aynalar: .

Kompakt (Lannér simpleks grupları)

Kompakt hiperbolik gruplara Lannér grupları denir. Folke Lannér onları ilk kez 1950'de inceleyen.^[7] Yalnızca 4. ve 5. sıra grafikleri olarak bulunurlar. Coxeter, 1954 tarihli makalesinde doğrusal hiperbolik coxeter gruplarını inceledi. Hiperbolik uzayda normal petekler,^[8] dahil hiperbolik 4-uzayda iki rasyonel çözüm: [5/2,5,3,3] = ve [5,5 / 2,5,3] = .

4. ve 5. Sıralar

İki çatallı gruptan birinin temel alanı, [5,3^1,1] ve [5,3,3^1,1], karşılık gelen doğrusal grubun iki katıdır, sırasıyla [5,3,4] ve [5,3,3,4]. Harf isimleri tarafından verilir Johnson uzatıldığı gibi Witt sembolleri.^[9]

Kompakt hiperbolik Coxeter grupları
Boyut H^d	Sıra	Toplam sayım	Doğrusal	Çatallanma	Döngüsel
H³	4	9	3: ${displaystyle {overline {BH}} _ {3}}$ = [4,3,5]: ${displaystyle {overline {K}} _ {3}}$ = [5,3,5]: ${displaystyle {overline {J}} _ {3}}$ = [3,5,3]:	${displaystyle {overline {DH}} _ {3}}$ = [5,3^1,1]:	${displaystyle {widehat {AB}} _ {3}}$ = [(3³,4)]: ${displaystyle {widehat {AH}} _ {3}}$ = [(3³,5)]: ${displaystyle {widehat {BB}} _ {3}}$ = [(3,4)^[2]]: ${displaystyle {widehat {BH}} _ {3}}$ = [(3,4,3,5)]: ${displaystyle {widehat {HH}} _ {3}}$ = [(3,5)^[2]]:
H⁴	5	5	3: ${displaystyle {overline {H}} _ {4}}$ = [3³,5]: ${displaystyle {overline {BH}} _ {4}}$ = [4,3,3,5]: ${displaystyle {overline {K}} _ {4}}$ = [5,3,3,5]:	${displaystyle {overline {DH}} _ {4}}$ = [5,3,3^1,1]:	${displaystyle {widehat {AF}} _ {4}}$ = [(3⁴,4)]:

Paracompact (Koszul simpleks grupları)

Bir örnek sıra-3 apeirogonal döşeme, {∞, 3} bir yeşil maymun ve sınırlı saat döngüsü

Paracompact (ayrıca noncompact olarak da adlandırılır) hiperbolik Coxeter grupları afin alt grupları içerir ve asimptotik simpleks temel alanlara sahiptir. En yüksek parakompakt hiperbolik Coxeter grubu 10. sıradadır. Bu gruplar Fransız matematikçinin adını almıştır. Jean-Louis Koszul.^[10] Bunlar aynı zamanda kompakt Lannér gruplarını genişleten yarı-Lannér grupları olarak da adlandırılır. Liste, M. Chein tarafından bilgisayar aramasıyla tamamlanmış ve 1969'da yayınlanmıştır.^[11]

Vinberg'e göre, bu 72 kompakt ve parakompakt basitliğin sekizi hariç tümü aritmetiktir. Aritmetik olmayan gruplardan ikisi kompakttır: ve . Diğer altı aritmetik olmayan grup, beş adet 3 boyutlu gruptan oluşan parakompakttır. , , , , ve ve bir 5 boyutlu grup .

İdeal basitlikler

İdeal temel alanlar

, [(∞, ∞, ∞)] Poincare disk modeli

İfade eden 5 hiperbolik Coxeter grubu vardır ideal basitlikler, herhangi bir düğümün çıkarılmasının afin bir Coxeter grubu ile sonuçlandığı grafikler. Bu nedenle, bu ideal simpleksin tüm köşeleri sonsuzdadır.^[12]

Sıra	İdeal grup	Afin alt grupları
3	[(∞,∞,∞)]	[∞]
4	[4^[4]]	[4,4]
4	[3^[3,3]]	[3^[3]]
4	[(3,6)^[2]]	[3,6]
6	[(3,3,4)^[2]]	[4,3,3,4], [3,4,3,3]	,

4-10. Sıralar

Sonsuz Öklid hücreleri gibi altıgen döşeme, uygun şekilde ölçeklendirilmiş, sonsuzda tek bir ideal noktaya yakınsar. altıgen döşeme petek, {6,3,3}, bu tek hücrede gösterildiği gibi Poincaré disk modeli projeksiyon.

Derece 4'ten 10'a kadar toplam 58 parakompakt hiperbolik Coxeter grubu vardır. 58'in tamamı aşağıda beş kategoride gruplandırılmıştır. Harf sembolleri tarafından verilir Johnson gibi Genişletilmiş Witt sembolleri, afin Witt sembollerinden PQRSTWUV kullanarak ve LMNOXYZ ekleyerek. Bu hiperbolik gruplara siklosşemler için bir üst çizgi veya bir şapka verilir. parantez gösterimi Coxeter'den Coxeter grubunun doğrusallaştırılmış bir temsilidir.

Hiperbolik parakompakt grupları
Sıra	Toplam sayım	Gruplar
4	23	${displaystyle {widehat {BR}} _ {3}}$ = [(3,3,4,4)]: ${displaystyle {widehat {CR}} _ {3}}$ = [(3,4³)]: ${displaystyle {widehat {RR}} _ {3}}$ = [4^[4]]: ${displaystyle {widehat {AV}} _ {3}}$ = [(3³,6)]: ${displaystyle {widehat {BV}} _ {3}}$ = [(3,4,3,6)]: ${displaystyle {widehat {HV}} _ {3}}$ = [(3,5,3,6)]: ${displaystyle {widehat {VV}} _ {3}}$ = [(3,6)^[2]]:	${displaystyle {overline {P}} _ {3}}$ = [3,3^[3]]: ${displaystyle {overline {BP}} _ {3}}$ = [4,3^[3]]: ${displaystyle {overline {HP}} _ {3}}$ = [5,3^[3]]: ${displaystyle {overline {VP}} _ {3}}$ = [6,3^[3]]: ${displaystyle {overline {DV}} _ {3}}$ = [6,3^1,1]: ${displaystyle {overline {O}} _ {3}}$ = [3,4^1,1]: ${displaystyle {overline {M}} _ {3}}$ = [4^1,1,1]:	${displaystyle {overline {R}} _ {3}}$ = [3,4,4]: ${displaystyle {overline {N}} _ {3}}$ = [4³]: ${displaystyle {overline {V}} _ {3}}$ = [3,3,6]: ${displaystyle {overline {BV}} _ {3}}$ = [4,3,6]: ${displaystyle {overline {HV}} _ {3}}$ = [5,3,6]: ${displaystyle {overline {Y}} _ {3}}$ = [3,6,3]: ${displaystyle {overline {Z}} _ {3}}$ = [6,3,6]:	${displaystyle {overline {DP}} _ {3}}$ = [3^{[] x []}]: ${displaystyle {overline {PP}} _ {3}}$ = [3^[3,3]]:
5	9	${displaystyle {overline {P}} _ {4}}$ = [3,3^[4]]: ${displaystyle {overline {BP}} _ {4}}$ = [4,3^[4]]: ${displaystyle {widehat {FR}} _ {4}}$ = [(3²,4,3,4)]: ${displaystyle {overline {DP}} _ {4}}$ = [3^{[3] x []}]:	${displaystyle {overline {N}} _ {4}}$ = [4,3,((4,2,3))]: ${displaystyle {overline {O}} _ {4}}$ = [3,4,3^1,1]: ${displaystyle {overline {S}} _ {4}}$ = [4,3^2,1]:	${displaystyle {overline {R}} _ {4}}$ = [(3,4)²]:	${displaystyle {overline {M}} _ {4}}$ = [4,3^1,1,1]:
6	12	${displaystyle {overline {P}} _ {5}}$ = [3,3^[5]]: ${displaystyle {widehat {AU}} _ {5}}$ = [(3⁵,4)]: ${displaystyle {widehat {AR}} _ {5}}$ = [(3,3,4)^[2]]:	${displaystyle {overline {S}} _ {5}}$ = [4,3,3^2,1]: ${displaystyle {overline {O}} _ {5}}$ = [3,4,3^1,1]: ${displaystyle {overline {N}} _ {5}}$ = [3,(3,4)^1,1]:	${displaystyle {overline {U}} _ {5}}$ = [3³,4,3]: ${displaystyle {overline {X}} _ {5}}$ = [3,3,4,3,3]: ${displaystyle {overline {R}} _ {5}}$ = [3,4,3,3,4]:	${displaystyle {overline {Q}} _ {5}}$ = [3^2,1,1,1]: ${displaystyle {overline {M}} _ {5}}$ = [4,3,3^1,1,1]: ${displaystyle {overline {L}} _ {5}}$ = [3^1,1,1,1,1]:
7	3	${displaystyle {overline {P}} _ {6}}$ = [3,3^[6]]:	${displaystyle {overline {Q}} _ {6}}$ = [3^1,1,3,3^2,1]:	${displaystyle {overline {S}} _ {6}}$ = [4,3²,3^2,1]:
8	4	${displaystyle {overline {P}} _ {7}}$ = [3,3^[7]]:	${displaystyle {overline {Q}} _ {7}}$ = [3^1,1,3²,3^2,1]:	${displaystyle {overline {S}} _ {7}}$ = [4,3³,3^2,1]:	${displaystyle {overline {T}} _ {7}}$ = [3^3,2,2]:
9	4	${displaystyle {overline {P}} _ {8}}$ = [3,3^[8]]:	${displaystyle {overline {Q}} _ {8}}$ = [3^1,1,3³,3^2,1]:	${displaystyle {overline {S}} _ {8}}$ = [4,3⁴,3^2,1]:	${displaystyle {overline {T}} _ {8}}$ = [3^4,3,1]:
10	4	${displaystyle {overline {P}} _ {9}}$ = [3,3^[9]]:	${displaystyle {overline {Q}} _ {9}}$ = [3^1,1,3⁴,3^2,1]:	${displaystyle {overline {S}} _ {9}}$ = [4,3⁵,3^2,1]:	${displaystyle {overline {T}} _ {9}}$ = [3^6,2,1]:

Parakompakt hiperbolik grupların alt grup ilişkileri

Bu ağaçlar, parakompakt hiperbolik grupların alt grup ilişkilerini temsil eder. Her bir bağlantıdaki alt grup endeksleri kırmızı ile verilmiştir.^[13] Dizin 2'nin alt grupları, bir ayna kaldırmayı ve temel alan ikiye katlamayı temsil eder. Diğerleri şu şekilde çıkarılabilir: uygunluk tetrahedral alanlar için (hacimlerin tam sayı oranı).

Alt grup ağaçları
H³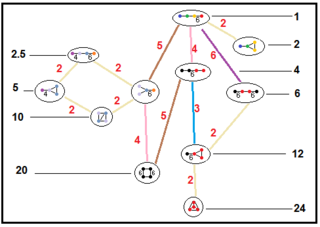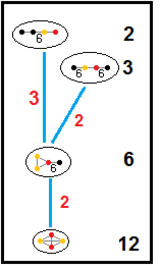
H⁴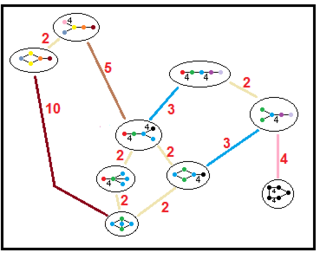
H⁵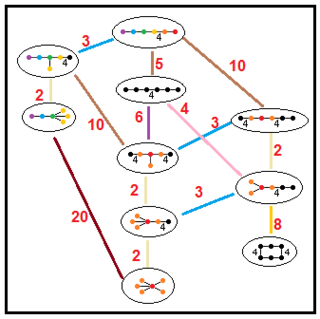

Hypercompact Coxeter grupları (Vinberg polytopes)

Tıpkı hiperbolik H düzlemi gibi² üçgen olmayan çokgen alanlara sahiptir, daha yüksek boyutlu yansıtıcı hiperbolik alanlar da mevcuttur. Bu basit olmayan alanlar, sonsuz sıra verilen kesişmeyen aynalar ile dejenere basitler olarak kabul edilebilir veya bir Coxeter diyagramında, bu tür dallara noktalı veya kesikli çizgiler verilir. Bunlar kararsız alanlar denir Vinberg politopları, sonra Ernest Vinberg onun için Vinberg'in algoritması hiperbolik bir yansıma grubunun basit olmayan temel alanını bulmak için. Geometrik olarak bu temel alanlar dörtgen olarak sınıflandırılabilir piramitler veya prizmalar veya diğeri politoplar iki aynanın kesişimi olarak kenarları olan iki yüzlü açı n = 2,3,4 ... için π / n olarak

Simpleks tabanlı bir alanda, nN boyutlu uzay için +1 aynalar. Simpleks olmayan alanlarda, n+1 aynalar. Liste sonludur, ancak tam olarak bilinmemektedir. Bunun yerine kısmi listeler şu şekilde numaralandırılmıştır: n+k k için aynalar 2,3 ve 4.

Üç boyutlu veya daha yüksek uzaydaki hiper kompakt Coxeter grupları, bir temel açıdan iki boyutlu gruplardan farklıdır. Aynı döngüsel sırayla aynı açılara sahip iki hiperbolik n-gon, farklı kenar uzunluklarına sahip olabilir ve genel olarak değildir. uyumlu. Tersine Vinberg politopları 3 veya daha büyük boyutlar tamamen dihedral açılarla belirlenir. Bu gerçek, Mostow sertlik teoremi, H'deki yansımalar tarafından üretilen iki izomorfik grupⁿ n> = 3 için, uyumlu temel alanları (Vinberg politopları) tanımlayın.

N boyutlu uzay için sıra n + 2 olan Vinberg politopları

Dereceli kompakt hiperbolik Vinberg politoplarının tam listesi n + 2 n-boyutları için aynalar, 1996 yılında F. Esselmann tarafından numaralandırılmıştır.^[14] Kısmi bir liste 1974'te I. M. Kaplinskaya tarafından yayınlandı.^[15]

Parakompakt çözümlerin tam listesi 2003 yılında P. Tumarkin tarafından 3 ila 17 boyutlarında yayınlandı.^[16]

H'deki en küçük parakompakt formu³ ile temsil edilebilir veya [∞, 3,3, ∞] parakompakt hiperbolik grubun [3,4,4] [3,4,1⁺, 4]. İkiye katlanmış temel alan, bir dörtyüzlü dörtgen bir piramide. Diğer piramitler arasında [4,4,1⁺,4] = [∞,4,4,∞], = . Döngüsel hiperbolik Coxeter grafiklerinin bazılarından bir aynayı kaldırmak, papyon grafiklerine dönüşür: [(3,3,4,1⁺, 4)] = [((3, ∞, 3)), ((3, ∞, 3))] veya , [(3,4,4,1⁺, 4)] = [((4, ∞, 3)), ((3, ∞, 4))] veya , [(4,4,4,1⁺, 4)] = [((4, ∞, 4)), ((4, ∞, 4))] veya .

Dörtgen piramit temel alanlara sahip diğer geçerli parakompakt grafikler şunları içerir:

Boyut	Sıra	Grafikler
H³	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Başka bir alt grup [1⁺,4^1,1,1] = [∞,4,1⁺,4,∞] = [∞^[6]]. = = .^[17]

N boyutlu uzay için sıra n + 3 olan Vinberg politopları

8 boyuta kadar sınırlı sayıda dejenere temel basitlik vardır. Dereceli Kompakt Vinberg politoplarının tam listesi n + 3 n-boyutlar için aynalar, 2004 yılında P. Tumarkin tarafından numaralandırılmıştır. Bu gruplar, ultra paralel dallar için noktalı / kesikli çizgilerle etiketlenmiştir. Dereceli Kompakt olmayan Vinberg politoplarının tam listesi n + 3 aynalar ve n-boyutlar için basit olmayan bir tepe noktası Mike Roberts tarafından numaralandırılmıştır.^[18]

4 ila 8 boyut için, sıra 7 ila 11 Coxeter grupları sırasıyla 44, 16, 3, 1 ve 1 olarak sayılır.^[19] En yüksek olanı 1984 yılında Bugaenko tarafından 8. boyut, 11. sırada keşfedildi:^[20]

Boyutlar	Sıra	Vakalar	Grafikler
H⁴	7	44	...
H⁵	8	16	..
H⁶	9	3
H⁷	10	1
H⁸	11	1

N boyutlu uzay için sıra n + 4 olan Vinberg politopları

8 boyuta kadar sınırlı sayıda dejenere temel basitlik vardır. Dereceli kompakt Vinberg politoplar n + 4 n boyutlu aynalar, 2005 yılında A. Felikson ve P. Tumarkin tarafından araştırılmıştır.^[21]

Lorentzian grupları

Lorentzian grupları ile normal petekler
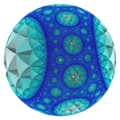{3,3,7} Poincare top modelinin dışında görüntülendi	{7,3,3} Poincare top modelinin dışında görüntülendi

Bu, [6,3,3,3] ve [6,3,6,3] 'den alt gruplar olarak düzenlenen rank 5 Lorentzian gruplarını gösterir. Son derece simetrik grup

, [3^[3,3,3]], [6,3,3,3] 'ün bir indeks 120 alt grubudur.

Simpleks alanları için Lorentzian grupları, parakompakt hiperbolik formların ötesinde grafikler olarak tanımlanabilir. Bunlar bazen süper ideal basitlikler olarak adlandırılır ve aynı zamanda bir Lorentz geometrisi, adını Hendrik Lorentz nın alanında özel ve Genel görelilik uzay-zaman, birini (veya daha fazlasını) içeren zaman gibi self dot ürünleri negatif olan boyutsal bileşenler.^[9] Danny Calegari bunları arar dışbükey koompakt N-boyutlu hiperbolik uzayda Coxeter grupları.^[22]^[23]

George Maxwell'in 1982 tarihli makalesi, Küre Paketler ve Hiperbolik Yansıma Grupları, Lorentzian'ın 5 ila 11. sıradaki sonlu listesini numaralandırır. Seviye 2yani 2 düğümün herhangi bir permütasyonunun kaldırılması sonlu veya Öklid grafiğini bırakır. Numaralandırması tamamlandı, ancak başka birinin alt grubu olan grafikleri listelemedi. Seviye-4'ün tüm yüksek dereceli kol Coxeter grupları Lorentzian'dır ve sınırda bir tam grafik 3-basit Coxeter-Dynkin diyagramı 6 sonsuz sıralı dallı, [∞^[3,3]]. Sıra 5-11, sırasıyla 186, 66, 36, 13, 10, 8 ve 4 Lorentzian grubuna sınırlı sayıda gruba sahiptir.^[24] H. Chen ve J.-P.'nin 2013 tarihli bir makalesi. Labbé, Lorentzian Coxeter grupları ve Boyd - Maxwell bilyalı salmastralar, yeniden hesaplandı ve tam listeyi yayınladı.^[25]

En yüksek sıralar 8-11 için tam listeler:

Lorentzian Coxeter grupları
Sıra	Toplam Miktar	Gruplar
4	∞	[3,3,7] ... [∞,∞,∞]: ... [4,3^[3]] ... [∞,∞^[3]]: ... [5,4^1,1] ... [∞^1,1,1]: ... ... [(5,4,3,3)] ... [∞^[4]]: ... ... ... [4^[]×[]] ... [∞^[]×[]]: ... ... [4^[3,3]] ... [∞^[3,3]]
5	186	...[3^[3,3,3]]:...
6	66
7	36	[3^1,1,1,1,1,1]: ...
8	13	[3,3,3^[6]]: [3,3^[6],3]: [3,3^[2+4],3]: [3,3^[1+5],3]: [3^{[] e × [3]}]:	[4,3,3,3^3,1]: [3^1,1,3,3^3,1]: [3,(3,3,4)^1,1]: [3^2,1,3,3^2,1]:		[4,3,3,3^2,2]: [3^1,1,3,3^2,2]:
9	10	[3,3^[3+4],3]: [3,3^[9]]: [3,3^[2+5],3]:	[3^2,1,3²,3^2,1]:	[3^3,1,3³,4]: [3^3,1,3,3,3^1,1]:	[3^3,3,2]: [3^2,2,4]: [3^2,2,3³,4]: [3^2,2,3,3,3^1,1]:
10	8	[3,3^[8],3]: [3,3^[3+5],3]: [3,3^[9]]:	[3^2,1,3³,3^2,1]:	[3^5,3,1]: [3^3,1,3⁴,4]: [3^3,1,3³,3^1,1]:	[3^4,4,1]:
11	4		[3^2,1,3⁴,3^2,1]:	[3^2,1,3⁶,4]: [3^2,1,3⁵,3^1,1]:	[3^7,2,1]:

Çok genişletilmiş Coxeter Diyagramları

Bir kullanım şunları içerir: çok geniş doğrudan tanım Dynkin diyagramı afin grupları olarak kabul eden kullanım Genişletilmişhiperbolik gruplar aşırı uzatılmışve üçüncü bir düğüm çok geniş basit gruplar. Bu uzantılar genellikle 1,2 veya 3 üssü ile işaretlenir + genişletilmiş düğüm sayısı için semboller. Bu genişleyen dizi, dallanma düğümünün kaldırılmasından sonra işlemin durmasına rağmen, grafikteki aynı konumdaki düğümleri sırayla kaldırarak geriye doğru uzatılabilir. E₈ geniş aile, E'den geriye doğru uzanan en yaygın gösterilen örnektir.₃ ve E'ye doğru₁₁.

Genişletme süreci, sonludan afine, hiperbolikten Lorentzian'a ilerleyen sınırlı bir Coxeter grafiği serisi tanımlayabilir. Cartan matrislerinin determinantı, serinin sonlu (pozitif) ile afin (sıfır) ile hiperbolik (negatif) arasında değiştiği yeri belirler ve en az bir hiperbolik alt grup içeren bir Lorentzian grubu olarak biter.^[26] Kristalografik olmayan H_n grupları, H'nin₄ kompakt bir hiperbolik olarak genişlemiş ve bir lorentzian grubuna aşırı genişlemiştir.

The determinant of the Schläfli matrix by rank are:^[27]

det(A₁ⁿ=[2^n-1]) = 2ⁿ (Finite for all n)
det(A_n=[3^n-1]) = n+1 (Finite for all n)
det(B_n=[4,3^n-2]) = 2 (Finite for all n)
det(D_n=[3^n-3,1,1]) = 4 (Finite for all n)

Determinants of the Schläfli matrix in exceptional series are:

det (E_n =[3^n-3,2,1]) = 9-n (Finite for E₃(=A₂Bir₁), E₄(=A₄), E₅(=D₅), E₆, E₇ ve E₈, affine at E₉ ( ${displaystyle {ilde {E}} _ {8}}$ ), hyperbolic at E₁₀)
det([3^n-4,3,1]) = 2(8-n) (Finite for n=4 to 7, affine ( ${displaystyle { ilde {E}}_{7}}$ ), and hyperbolic at n=8.)
det([3^n-4,2,2]) = 3(7-n) (Finite for n=4 to 6, affine ( ${displaystyle { ilde {E}}_{6}}$ ), and hyperbolic at n=7.)
det(F_n=[3,4,3^n-3]) = 5-n (Finite for F₃(=B₃) için F₄, affine at F₅ ( ${displaystyle {ilde {F}} _ {4}}$ ), hyperbolic at F₆)
det(G_n=[6,3^n-2]) = 3-n (Finite for G₂, affine at G₃ ( ${displaystyle {ilde {G}} _ {2}}$ ), hyperbolic at G₄)

Smaller extended series
Sonlu	${displaystyle A_{2}}$	${displaystyle C_ {2}}$	${displaystyle G_{2}}$	${displaystyle A_{3}}$	${displaystyle B_{3}}$	${displaystyle C_{3}}$	${displaystyle H_ {4}}$
Rank n	[3^[3],3^n-3]	[4,4,3^n-3]	G_n=[6,3^n-2]	[3^[4],3^n-4]	[4,3^1,n-3]	[4,3,4,3^n-4]	H_n=[5,3^n-2]
2	[3] Bir₂	[4] C₂	[6] G₂		[2] Bir₁²	[4] C₂	[5] H₂
3	[3^[3]] Bir₂⁺= ${displaystyle {ilde {A}} _ {2}}$	[4,4] C₂⁺= ${displaystyle { ilde {C}}_{2}}$	[6,3] G₂⁺= ${displaystyle {ilde {G}} _ {2}}$	[3,3]=A₃	[4,3] B₃	[4,3] C₃	[5,3] H₃
4	[3^[3],3] Bir₂⁺⁺= ${displaystyle {overline {P}}_{3}}$	[4,4,3] C₂⁺⁺= ${displaystyle {overline {R}}_{3}}$	[6,3,3] G₂⁺⁺= ${displaystyle {overline {V}}_{3}}$	[3^[4]] Bir₃⁺= ${displaystyle {ilde {A}} _ {3}}$	[4,3^1,1] B₃⁺= ${displaystyle { ilde {B}}_{3}}$	[4,3,4] C₃⁺= ${displaystyle { ilde {C}}_{3}}$	[5,3,3] H₄
5	[3^[3],3,3] Bir₂⁺⁺⁺	[4,4,3,3] C₂⁺⁺⁺	[6,3,3,3] G₂⁺⁺⁺	[3^[4],3] Bir₃⁺⁺= ${displaystyle {overline {P}}_{4}}$	[4,3^2,1] B₃⁺⁺= ${displaystyle {overline {S}}_{4}}$	[4,3,4,3] C₃⁺⁺= ${displaystyle {overline {R}}_{4}}$	[5,3³] H₅= ${displaystyle {overline {H}}_{4}}$
6				[3^[4],3,3] Bir₃⁺⁺⁺	[4,3^3,1] B₃⁺⁺⁺	[4,3,4,3,3] C₃⁺⁺⁺	[5,3⁴] H₆
Det(M_n)	3(3-n)	2(3-n)	3-n	4(4-n)	2(4-n)

Middle extended series
Sonlu	${displaystyle A_{4}}$	${displaystyle B_{4}}$	${displaystyle C_ {4}}$	${displaystyle D_{4}}$	${displaystyle F_{4}}$	${displaystyle A_{5}}$	${displaystyle B_{5}}$	${displaystyle D_{5}}$
Rank n	[3^[5],3^n-5]	[4,3,3^n-4,1]	[4,3,3,4,3^n-5]	[3^n-4,1,1,1]	[3,4,3^n-3]	[3^[6],3^n-6]	[4,3,3,3^n-5,1]	[3^1,1,3,3^n-5,1]
3		[4,3^−1,1] B₂Bir₁	[4,3] B₃	[3^−1,1,1,1] Bir₁³	[3,4] B₃		[4,3,3] C₃
4	[3³] Bir₄	[4,3,3] B₄	[4,3,3] C₄	[3^0,1,1,1] D₄	[3,4,3] F₄		[4,3,3,3^−1,1] B₃Bir₁	[3^1,1,3,3^−1,1] Bir₃Bir₁
5	[3^[5]] Bir₄⁺= ${displaystyle {ilde {A}} _ {4}}$	[4,3,3^1,1] B₄⁺= ${displaystyle { ilde {B}}_{4}}$	[4,3,3,4] C₄⁺= ${displaystyle { ilde {C}}_{4}}$	[3^1,1,1,1] D₄⁺= ${displaystyle { ilde {D}}_{4}}$	[3,4,3,3] F₄⁺= ${displaystyle {ilde {F}} _ {4}}$	[3⁴] Bir₅	[4,3,3,3,3] B₅	[3^1,1,3,3] D₅
6	[3^[5],3] Bir₄⁺⁺= ${displaystyle {overline {P}}_{5}}$	[4,3,3^2,1] B₄⁺⁺= ${displaystyle {overline {S}}_{5}}$	[4,3,3,4,3] C₄⁺⁺= ${displaystyle {overline {R}}_{5}}$	[3^2,1,1,1] D₄⁺⁺= ${displaystyle {overline {Q}}_{5}}$	[3,4,3³] F₄⁺⁺= ${displaystyle {overline {U}}_{5}}$	[3^[6]] Bir₅⁺= ${displaystyle {ilde {A}} _ {5}}$	[4,3,3,3^1,1] B₅⁺= ${displaystyle {ilde {B}} _ {5}}$	[3^1,1,3,3^1,1] D₅⁺= ${displaystyle {ilde {D}} _ {5}}$
7	[3^[5],3,3] Bir₄⁺⁺⁺	[4,3,3^3,1] B₄⁺⁺⁺	[4,3,3,4,3,3] C₄⁺⁺⁺	[3^3,1,1,1] D₄⁺⁺⁺	[3,4,3⁴] F₄⁺⁺⁺	[3^[6],3] Bir₅⁺⁺= ${displaystyle {overline {P}}_{6}}$	[4,3,3,3^2,1] B₅⁺⁺= ${displaystyle {overline {S}}_{6}}$	[3^1,1,3,3^2,1] D₅⁺⁺= ${displaystyle {overline {Q}}_{6}}$
8						[3^[6],3,3] Bir₅⁺⁺⁺	[4,3,3,3^3,1] B₅⁺⁺⁺	[3^1,1,3,3^3,1] D₅⁺⁺⁺
Det(M_n)	5(5-n)	2(5-n)		4(5-n)	5-n	6(6-n)	4(6-n)

Some higher extended series
Sonlu	${displaystyle A_ {6}}$	${displaystyle B_{6}}$	${displaystyle D_{6}}$	${displaystyle E_{6}}$	${displaystyle A_ {7}}$	${displaystyle B_{7}}$	${displaystyle D_ {7}}$	${displaystyle E_{7}}$	${displaystyle E_{8}}$
Rank n	[3^[7],3^n-7]	[4,3³,3^n-6,1]	[3^1,1,3,3,3^n-6,1]	[3^n-5,2,2]	[3^[8],3^n-8]	[4,3⁴,3^n-7,1]	[3^1,1,3,3,3,3^n-7,1]	[3^n-5,3,1]	E_n=[3^n-4,2,1]
3									[3^−1,2,1] E₃=A₂Bir₁
4				[3^−1,2,2] Bir₂²				[3^−1,3,1] Bir₃Bir₁	[3^0,2,1] E₄=A₄
5		[4,3,3,3,3^−1,1] B₄Bir₁	[3^1,1,3,3,3^−1,1] D₄Bir₁	[3^0,2,2] Bir₅				[3^0,3,1] Bir₅	[3^1,2,1] E₅= D₅
6	[3⁵] Bir₆	[4,3⁴] B₆	[3^1,1,3,3,3] D₆	[3^1,2,2] E₆		[4,3,3,3,3,3^−1,1] B₅Bir₁	[3^1,1,3,3,3,3^−1,1] D₅Bir₁	[3^1,3,1] D₆	[3^2,2,1] E₆ *
7	[3^[7]] Bir₆⁺= ${displaystyle { ilde {A}}_{6}}$	[4,3³,3^1,1] B₆⁺= ${displaystyle { ilde {B}}_{6}}$	[3^1,1,3,3,3^1,1] D₆⁺= ${displaystyle { ilde {D}}_{6}}$	[3^2,2,2] E₆⁺= ${displaystyle { ilde {E}}_{6}}$	[3⁶] Bir₇	[4,3⁵] B₇	[3^1,1,3,3,3,3^0,1] D₇	[3^2,3,1] E₇ *	[3^3,2,1] E₇ *
8	[3^[7],3] Bir₆⁺⁺= ${displaystyle {overline {P}}_{7}}$	[4,3³,3^2,1] B₆⁺⁺= ${displaystyle {overline {S}}_{7}}$	[3^1,1,3,3,3^2,1] D₆⁺⁺= ${displaystyle {overline {Q}}_{7}}$	[3^3,2,2] E₆⁺⁺= ${displaystyle {overline {T}}_{7}}$	[3^[8]] Bir₇⁺= ${displaystyle {ilde {A}} _ {7}}$ *	[4,3⁴,3^1,1] B₇⁺= ${displaystyle {ilde {B}} _ {7}}$ *	[3^1,1,3,3,3,3^1,1] D₇⁺= ${displaystyle {ilde {D}} _ {7}}$ *	[3^3,3,1] E₇⁺= ${displaystyle { ilde {E}}_{7}}$ *	[3^4,2,1] E₈ *
9	[3^[7],3,3] Bir₆⁺⁺⁺	[4,3³,3^3,1] B₆⁺⁺⁺	[3^1,1,3,3,3^3,1] D₆⁺⁺⁺	[3^4,2,2] E₆⁺⁺⁺	[3^[8],3] Bir₇⁺⁺= ${displaystyle {overline {P}}_{8}}$ *	[4,3⁴,3^2,1] B₇⁺⁺= ${displaystyle {overline {S}}_{8}}$ *	[3^1,1,3,3,3,3^2,1] D₇⁺⁺= ${displaystyle {overline {Q}}_{8}}$ *	[3^4,3,1] E₇⁺⁺= ${displaystyle {overline {T}}_{8}}$ *	[3^5,2,1] E₉= E₈⁺= ${displaystyle {ilde {E}} _ {8}}$ *
10					[3^[8],3,3] Bir₇⁺⁺⁺ *	[4,3⁴,3^3,1] B₇⁺⁺⁺ *	[3^1,1,3,3,3,3^3,1] D₇⁺⁺⁺ *	[3^5,3,1] E₇⁺⁺⁺ *	[3^6,2,1] E₁₀= E₈⁺⁺= ${displaystyle {overline {T}}_{9}}$ *
11									[3^7,2,1] E₁₁= E₈⁺⁺⁺ *
Det(M_n)	7(7-n)	2(7-n)	4(7-n)	3(7-n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

Geometric folding

Finite and affine foldings^[28]
φ_Bir : Bir_Γ --> A_Γ' for finite types
Γ	Γ'	Folding description	Coxeter-Dynkin diyagramları
ben₂(h )	Γ(h)	Dihedral folding
B_n	Bir_2n	(I,s_n)
B_n	D_{n + 1}, Bir_2n-1	(Bir₃,+/-ε)
F₄	E₆	(Bir₃,±ε)
H₄	E₈	(Bir₄,±ε)
H₃	D₆
H₂	Bir₄
G₂	Bir₅	(Bir₅,±ε)
G₂	D₄	(D₄,±ε)
φ: A_Γ⁺ --> A_Γ'⁺ for affine types
${displaystyle {ilde {A}} _ {n-1}}$	${displaystyle { ilde {A}}_{kn-1}}$	Yerel olarak önemsiz
${displaystyle { ilde {B}}_{n}}$	${displaystyle { ilde {D}}_{2n+1}}$	(I,s_n)
${displaystyle { ilde {B}}_{n}}$	${displaystyle { ilde {D}}_{n+1}}$ , ${displaystyle { ilde {D}}_{2n}}$	(Bir₃,±ε)
${displaystyle { ilde {C}}_{n}}$	${displaystyle { ilde {B}}_{n+1}}$ , ${displaystyle { ilde {C}}_{2n}}$	(Bir₃,±ε)
${displaystyle { ilde {C}}_{n}}$	${displaystyle { ilde {C}}_{2n+1}}$	(I,s_n)
${displaystyle { ilde {C}}_{n}}$	${displaystyle { ilde {A}}_{2n+1}}$	(I,s_n) & (I,s₀)
	${displaystyle { ilde {A}}_{2n}}$	(Bir₃,ε) & (I,s₀)
	${displaystyle { ilde {A}}_{2n-1}}$	(Bir₃,ε) & (A₃,ε')
${displaystyle { ilde {C}}_{n}}$	${displaystyle { ilde {D}}_{n+2}}$	(Bir₃,-ε) & (A₃,-ε')
${displaystyle { ilde {C}}_{2}}$	${displaystyle {ilde {D}} _ {5}}$	(I,s₁)
${displaystyle {ilde {F}} _ {4}}$	${displaystyle { ilde {E}}_{6}}$ , ${displaystyle { ilde {E}}_{7}}$	(Bir₃,±ε)
${displaystyle {ilde {G}} _ {2}}$	${displaystyle { ilde {D}}_{6}}$ , ${displaystyle { ilde {E}}_{7}}$	(Bir₅,±ε)
	${displaystyle { ilde {B}}_{3}}$ , ${displaystyle {ilde {F}} _ {4}}$	(B₃,±ε)
	${displaystyle { ilde {D}}_{4}}$ , ${displaystyle { ilde {E}}_{6}}$	(D₄,±ε)

A (simply-laced) Coxeter–Dynkin diagram (finite, afin, or hyperbolic) that has a symmetry (satisfying one condition, below) can be quotiented by the symmetry, yielding a new, generally multiply laced diagram, with the process called "folding".^[29]^[30]

For example, in D₄ G'ye katlama₂, G'deki kenar₂ 3 dış düğümün sınıfından (değerlik 1), merkezi düğümün sınıfına (değerlik 3). Ve E₈ folds into 2 copies of H₄, the second copy scaled by τ.^[31]

Geometrically this corresponds to ortogonal projeksiyonlar nın-nin tek tip politoplar and tessellations. Notably, any finite simply-laced Coxeter–Dynkin diagram can be folded to I₂(h), nerede h ... Coxeter numarası, which corresponds geometrically to a projection to the Coxeter düzlemi.

A few hyperbolic foldings

Karmaşık yansımalar

Coxeter–Dynkin diagrams have been extended to karmaşık alan, Cⁿ where nodes are unitary reflections of period greater than 2. Nodes are labeled by an index, assumed to be 2 for ordinary real reflection if suppressed. Coxeter writes the complex group, p[q]r, as diagram .^[32]

A 1-dimensional düzenli karmaşık politop içinde ${displaystyle mathbb {C} ^{1}}$ is represented as sahip olmak p köşeler. Its real representation is a normal çokgen, {p}. Simetrisi _p[] or , sipariş p. Bir üniter operatör generator for is seen as a rotation in ${displaystyle mathbb {R} ^ {2}}$ by 2π/p radyan counter clockwise ve bir edge is created by sequential applications of a single unitary reflection. A unitary reflection generator for a 1-polytope with p köşeler $e 2π ben / p = cos(2π/ p) + ben sin(2π/ p)$ . Ne zaman p = 2, the generator is e^πben = –1, the same as a nokta yansıması gerçek düzlemde.

In a higher polytope, _p{} or temsil eder p-edge element, with a 2-edge, {} or , representing an ordinary real edge between two vertices.

Regular complex 1-polytopes
Complex 1-polytopes, temsil edilen Argand uçağı as regular polygons for p = 2, 3, 4, 5, and 6, with black vertices. The centroid of the p vertices is shown seen in red. The sides of the polygons represent one application of the symmetry generator, mapping each vertex to the next counterclockwise copy. These polygonal sides are not edge elements of the polytope, as a complex 1-polytope can have no edges (it often dır-dir a complex edge) and only contains vertex elements.

12 irreducible Shephard groups with their subgroup index relations.^[33] Subgroups index 2 relate by removing a real reflection: _p[2q]₂ --> _p[q]_p, index 2. _p[4]_q --> _p[q]_p, dizin q.	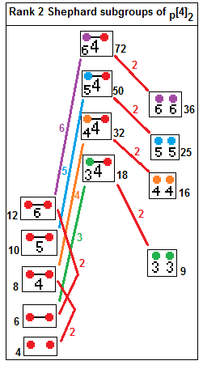_p[4]₂ subgroups: p=2,3,4... _p[4]₂ --> [p], index p _p[4]₂ --> _p[]×_p[], index 2

Aa düzenli karmaşık çokgenler içinde ${displaystyle mathbb {C} ^{2}}$ , has the form _p{q}_r or Coxeter diagram . The symmetry group of a regular complex polygon is not called a Coxeter grubu ama bunun yerine Shephard group, bir tür Karmaşık yansıma grubu. Sırası _p[q]_r dır-dir ${displaystyle 8/qcdot (1/p+2/q+1/r-1)^{-2}}$ .^[34]

The rank 2 Shephard groups are: ₂[q]₂, _p[4]₂, ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, ve ₅[4]₃ veya , , , , , , , , , , , , , of order 2q, 2p², 24, 48, 72, 96, 144, 192, 288, 360, 600, 1200, and 1800 respectively.

The symmetry group _p₁[q]_p₂ is represented by 2 generators R₁, R₂, where: R₁^p₁ = R₂^p₂ = I. If q is even, (R₂R₁)^q/2 = (R₁R₂)^q/2. Eğer q is odd, (R₂R₁)^(q-1)/2R₂ = (R₁R₂)^(q-1)/2R₁. Ne zaman q garip, p₁=p₂.

${displaystyle mathbb {C} ^ {3}}$ grup or [1 1 1]^p is defined by 3 period 2 unitary reflections {R₁, R₂, R₃}: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₁)^p = 1. The period p olarak görülebilir çift dönüş Gerçek olarak ${displaystyle mathbb {R} ^ {4}}$ .

Benzer ${displaystyle mathbb {C} ^ {3}}$ grup or [1 1 1]^(p) is defined by 3 period 2 unitary reflections {R₁, R₂, R₃}: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₂)^p = 1.

Ayrıca bakınız

Referanslar

^ Hall, Brian C. (2003), Lie Grupları, Lie Cebirleri ve Gösterimler: Temel GirişSpringer, ISBN 978-0-387-40122-5
^ Coxeter, Normal Politoplar, (3. baskı, 1973), Dover baskısı, ISBN 0-486-61480-8, Sec 7.7. page 133, Schläfli's Criterion
^ Lannér F., On complexes with transitive groups of automorphisms, Medd. Lunds Üniv. Mat. Sem. [Comm. Sem. Matematik. Üniv. Lund], 11 (1950), 1–71
^ Allcock, Daniel (11 July 2006). "Infinitely many hyperbolic Coxeter groups through dimension 19". Geometri ve Topoloji. 10 (2): 737–758. arXiv:0903.0138. doi:10.2140/gt.2006.10.737.
^ Coxeter Gruplarının Geometrisi ve Topolojisi, Michael W. Davis, 2008 s. 105 Table 6.2. Hyperbolic diagrams
^ Takeuchi, Kisao (January 1977). "TAKEUCHI : Arithmetic triangle groups". Japonya Matematik Derneği Dergisi. Projecteuclid.org. 29 (1): 91–106. doi:10.2969/jmsj/02910091. Alındı 2013-07-05.
^ Folke Lannér, On complexes with transitive groups of automorphisms, Comm. Sém., Math. Üniv. Lund [Medd. Lunds Üniv. Mat. Sem.] 11 (1950) [1]
^ Regular Honeycombs in hyperbolic space, Coxeter, 1954
^ ^a ^b Norman Johnson, Geometries and Transformations (2018), Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices
^ J. L. Koszul, Lectures on hyperbolic Coxeter groups, University of Notre Dame (1967)
^ M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d’ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), no. Ser. R-3, 3–16 (French). [2]
^ Subalgebras of hyperbolic Kay-Moody algebras, Figure 5.1, p.13
^ Johnson, N.W.; Kellerhals, R.; Ratcliffe, J.G.; Tschantz, S.T. (2002). "Commensurability classes of hyperbolic Coxeter groups". Doğrusal Cebir ve Uygulamaları. 345 (1–3): 119–147. doi:10.1016/S0024-3795(01)00477-3.
^ F. Esselmann, The classification of compact hyperbolic Coxeter d-polytopes with d+2 facets. Yorum Yap. Matematik. Helvetici 71 (1996), 229–242. [3]
^ I. M. Kaplinskaya, Discrete groups generated by reflections in the faces of simplicial prisms in Lobachevskian spaces. Matematik. Notes,15 (1974), 88–91. [4]
^ P. Tumarkin, Hyperbolic Coxeter n-polytopes with n+2 facets (2003)
^ Norman W. Johnson and Asia Ivic Weiss, Quadratic Integers and Coxeter Groups, Can. J. Math. Cilt 51 (6), 1999 pp. 1307–1336 [5]
^ [6] A Classification of Non-Compact Coxeter Polytopes with n+3 Facets and One Non-Simple Vertex
^ P. Tumarkin, Compact hyperbolic Coxeter (2004)
^ V. O. Bugaenko, Groups of automorphisms of unimodular hyperbolic quadratic forms over the ring Zh√5+12 ben. Moscow Univ. Matematik. Boğa. 39 (1984), 6-14.
^ Anna Felikson, Pavel Tumarkin, On compact hyperbolic Coxeter d-polytopes with d+4 facets, 2005 [7]
^ Random groups, diamonds and glass, Danny Calegari of the University of Chicago, June 25, 2014 at the Bill Thurston Legacy Conference
^ Coxeter groups and random groups, Danny Calegari, last revised 4 Apr 2015
^ Maxwell, George (1982). "Sphere packings and hyperbolic reflection groups". Cebir Dergisi. 79: 78–97. doi:10.1016/0021-8693(82)90318-0.
^ Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, https://arxiv.org/abs/1310.8608
^ Kac-Moody Algebras in M-theory
^ Cartan–Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982
^ John Crisp, 'Injective maps arasında Artin grupları ', in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Arşivlendi 2005-10-16 at the Wayback Makinesi, pp 13-14, and googlebook, Geometric group theory down under, p 131
^ Zuber, Jean-Bernard (1998). "Generalized Dynkin diagrams and root systems and their folding". Topological Field Theory: 28–30. arXiv:hep-th/9707046. Bibcode:1998tftp.conf..453Z. CiteSeerX 10.1.1.54.3122.
^ Dechant, Pierre-Philippe; Boehm, Celine; Twarock, Reidun (2013). "Affine extensions of non-crystallographic Coxeter groups induced by projection". Matematiksel Fizik Dergisi. 54 (9): 093508. arXiv:1110.5228. Bibcode:2013JMP....54i3508D. doi:10.1063/1.4820441.
^ The E8 Geometry from a Clifford Perspective Uygulamalı Clifford Cebirlerinde Gelişmeler, March 2017, Volume 27, Issue 1, pp 397–421 Pierre-Philippe Dechant
^ Coxeter, Karmaşık Düzenli Politoplar, second edition, (1991)
^ Coxeter, Complex Regular Polytopes, p. 177, Table III
^ Unitary Reflection Groups, s. 87

daha fazla okuma

James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
Kaleidoscopes: H.S.M.'nin Seçilmiş Yazıları CoxeterF. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Yayını, 1995, ISBN 978-0-471-01003-6 [8], Googlebooks [9]
- (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
Coxeter, Geometrinin Güzelliği: On İki DenemeDover Yayınları, 1999, ISBN 978-0-486-40919-1 (Bölüm 3: Wythoff'un Tek Biçimli Politop Yapısı)
Coxeter, Normal Politoplar (1963), Macmillan Şirketi
- Normal Politoplar, Üçüncü baskı, (1973), Dover baskısı, ISBN 0-486-61480-8 (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
H.S.M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980
Norman Johnson, Geometries and Transformations, Chapters 11,12,13, preprint 2011
N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Dönüşüm Grupları 1999, Cilt 4, Sayı 4, s. 329–353 [10] [11]
Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups PDF Yapabilmek. J. Math. Cilt 51 (6), 1999 pp. 1307–1336

Dış bağlantılar

Weisstein, Eric W. "Coxeter–Dynkin diagram". MathWorld.
October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in Toronto, Kanada; Eugene Dynkin Collection of Mathematics Interviews, Cornell Üniversitesi Kütüphanesi.

[1] Hall, Brian C. (2003), Lie Grupları, Lie Cebirleri ve Gösterimler: Temel GirişSpringer, ISBN 978-0-387-40122-5

[2] Coxeter, Normal Politoplar, (3. baskı, 1973), Dover baskısı, ISBN 0-486-61480-8, Sec 7.7. page 133, Schläfli's Criterion

[3] Lannér F., On complexes with transitive groups of automorphisms, Medd. Lunds Üniv. Mat. Sem. [Comm. Sem. Matematik. Üniv. Lund], 11 (1950), 1–71

[4] Allcock, Daniel (11 July 2006). "Infinitely many hyperbolic Coxeter groups through dimension 19". Geometri ve Topoloji. 10 (2): 737–758. arXiv:0903.0138. doi:10.2140/gt.2006.10.737.

[5] Coxeter Gruplarının Geometrisi ve Topolojisi, Michael W. Davis, 2008 s. 105 Table 6.2. Hyperbolic diagrams

[6] Takeuchi, Kisao (January 1977). "TAKEUCHI : Arithmetic triangle groups". Japonya Matematik Derneği Dergisi. Projecteuclid.org. 29 (1): 91–106. doi:10.2969/jmsj/02910091. Alındı 2013-07-05.

[7] Folke Lannér, On complexes with transitive groups of automorphisms, Comm. Sém., Math. Üniv. Lund [Medd. Lunds Üniv. Mat. Sem.] 11 (1950) [1]

[8] Regular Honeycombs in hyperbolic space, Coxeter, 1954

[johnson2018-9] Norman Johnson, Geometries and Transformations (2018), Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices

[10] J. L. Koszul, Lectures on hyperbolic Coxeter groups, University of Notre Dame (1967)

[11] M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d’ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), no. Ser. R-3, 3–16 (French). [2]

[12] Subalgebras of hyperbolic Kay-Moody algebras, Figure 5.1, p.13

[13] Johnson, N.W.; Kellerhals, R.; Ratcliffe, J.G.; Tschantz, S.T. (2002). "Commensurability classes of hyperbolic Coxeter groups". Doğrusal Cebir ve Uygulamaları. 345 (1–3): 119–147. doi:10.1016/S0024-3795(01)00477-3.

[14] F. Esselmann, The classification of compact hyperbolic Coxeter d-polytopes with d+2 facets. Yorum Yap. Matematik. Helvetici 71 (1996), 229–242. [3]

[15] I. M. Kaplinskaya, Discrete groups generated by reflections in the faces of simplicial prisms in Lobachevskian spaces. Matematik. Notes,15 (1974), 88–91. [4]

[16] P. Tumarkin, Hyperbolic Coxeter n-polytopes with n+2 facets (2003)

[17] Norman W. Johnson and Asia Ivic Weiss, Quadratic Integers and Coxeter Groups, Can. J. Math. Cilt 51 (6), 1999 pp. 1307–1336 [5]

[18] [6] A Classification of Non-Compact Coxeter Polytopes with n+3 Facets and One Non-Simple Vertex

[19] P. Tumarkin, Compact hyperbolic Coxeter (2004)

[20] V. O. Bugaenko, Groups of automorphisms of unimodular hyperbolic quadratic forms over the ring Zh√5+12 ben. Moscow Univ. Matematik. Boğa. 39 (1984), 6-14.

[21] Anna Felikson, Pavel Tumarkin, On compact hyperbolic Coxeter d-polytopes with d+4 facets, 2005 [7]

[22] Random groups, diamonds and glass, Danny Calegari of the University of Chicago, June 25, 2014 at the Bill Thurston Legacy Conference

[23] Coxeter groups and random groups, Danny Calegari, last revised 4 Apr 2015

[24] Maxwell, George (1982). "Sphere packings and hyperbolic reflection groups". Cebir Dergisi. 79: 78–97. doi:10.1016/0021-8693(82)90318-0.

[25] Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, https://arxiv.org/abs/1310.8608

[26] Kac-Moody Algebras in M-theory

[27] Cartan–Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982

[28] John Crisp, 'Injective maps arasında Artin grupları ', in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Arşivlendi 2005-10-16 at the Wayback Makinesi, pp 13-14, and googlebook, Geometric group theory down under, p 131

[29] Zuber, Jean-Bernard (1998). "Generalized Dynkin diagrams and root systems and their folding". Topological Field Theory: 28–30. arXiv:hep-th/9707046. Bibcode:1998tftp.conf..453Z. CiteSeerX 10.1.1.54.3122.

[30] Dechant, Pierre-Philippe; Boehm, Celine; Twarock, Reidun (2013). "Affine extensions of non-crystallographic Coxeter groups induced by projection". Matematiksel Fizik Dergisi. 54 (9): 093508. arXiv:1110.5228. Bibcode:2013JMP....54i3508D. doi:10.1063/1.4820441.

[31] The E8 Geometry from a Clifford Perspective Uygulamalı Clifford Cebirlerinde Gelişmeler, March 2017, Volume 27, Issue 1, pp 397–421 Pierre-Philippe Dechant

[32] Coxeter, Karmaşık Düzenli Politoplar, second edition, (1991)

[33] Coxeter, Complex Regular Polytopes, p. 177, Table III

[34] Unitary Reflection Groups, s. 87

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]