Yenileme teorisi - Renewal theory

Yenileme teorisi şubesi olasılık teorisi genelleyen Poisson süreci keyfi bekletme süreleri için. Onun yerine üssel olarak dağıtılmış bekletme süreleri, bir yenileme sürecinde herhangi bir bağımsız ve aynı şekilde dağıtılmış (IID) sonlu ortalamaya sahip tutma süreleri. Yenileme-ödül süreci ayrıca, IID olan ancak bekletme sürelerinden bağımsız olması gerekmeyen her bekletme süresinde oluşan rastgele bir ödül dizisine sahiptir.

Bir yenileme sürecinin asimptotik özellikleri vardır. büyük sayıların güçlü kanunu ve Merkezi Limit Teoremi. Yenileme işlevi ${ displaystyle m (t)}$ (beklenen varış sayısı) ve ödül işlevi ${ displaystyle g (t)}$ (beklenen ödül değeri) yenileme teorisinde kilit öneme sahiptir. Yenileme fonksiyonu yinelemeli bir integral denklemi, yenileme denklemini karşılar. Anahtar yenileme denklemi, sınırlayıcı değerini verir. kıvrım nın-nin ${ displaystyle m '(t)}$ uygun bir negatif olmayan işleve sahip. Yenileme süreçlerinin üst üste binmesi özel bir durum olarak incelenebilir. Markov yenileme süreçleri.

Uygulamalar, bir fabrikadaki yıpranmış makinelerin değiştirilmesi için en iyi stratejinin hesaplanmasını ve farklı sigorta poliçelerinin uzun vadeli faydalarının karşılaştırılmasını içerir. Teftiş paradoksu, zaman zaman bir yenileme aralığının gözlemlenmesiyle ilgilidir. t ortalama değeri, ortalama yenileme aralığından daha büyük olan bir aralık verir.

Yenileme süreçleri

Giriş

yenileme süreci bir genellemedir Poisson süreci. Temelde, Poisson süreci bir sürekli zamanlı Markov süreci pozitif tamsayılarda (genellikle sıfırdan başlar) bağımsız olan üssel olarak dağıtılmış her tam sayıdaki tutma süreleri ${ displaystyle i}$ bir sonraki tam sayıya geçmeden önce, ${ displaystyle i + 1}$. Bir yenileme sürecinde, bekletme sürelerinin üstel bir dağılıma sahip olması gerekmez; daha ziyade, bekletme süreleri bağımsız ve aynı şekilde dağıtıldığı sürece, bekletme süreleri pozitif sayılarda herhangi bir dağılım gösterebilir (IID ) ve sonlu ortalamaya sahiptir.

Resmi tanımlama

Yenileme sürecinin örnek evrimi ile tutma süreleri S_ben ve zıplama zamanları J_n.

İzin Vermek ${ displaystyle S_ {1}, S_ {2}, S_ {3}, S_ {4}, S_ {5}, ldots}$ pozitif bir dizi olmak bağımsız aynı şekilde dağıtılmış rastgele değişkenler öyle ki

${ displaystyle 0 < operatorname {E} [S_ {i}] < infty.}$

Rastgele değişkene atıfta bulunuyoruz ${ displaystyle S_ {i}}$ "olarak${ displaystyle i}$bekletme süresi ".

${ displaystyle operatöradı {E} [S_ {i}]}$ ... beklenti nın-nin ${ displaystyle S_ {i}}$.

Her biri için tanımla n > 0 :

${ displaystyle J_ {n} = toplam _ {i = 1} ^ {n} S_ {i},}$

her biri ${ displaystyle J_ {n}}$ "${ displaystyle n}$-nci atlama zamanı "ve aralıklar ${ displaystyle [J_ {n}, J_ {n + 1}]}$ "yenileme aralıkları" olarak adlandırılır.

Sonra ${ displaystyle (X_ {t}) _ {t geq 0}}$ rastgele değişkenle verilir

${ displaystyle X_ {t} = toplam _ {n = 1} ^ { infty} operatorname { mathbb {I}} _ { {J_ {n} leq t }} = sup sol {, ​​n: J_ {n} leq t , sağ }}$

nerede ${ displaystyle operatorname { mathbb {I}} _ { {J_ {n} leq t }}}$ ... gösterge işlevi

${ displaystyle operatorname { mathbb {I}} _ { {J_ {n} leq t }} = { begin {case} 1 ve { text {if}} J_ {n} leq t 0 ve { text {aksi}} end {vakalar}}}$

${ displaystyle (X_ {t}) _ {t geq 0}}$ zamana göre meydana gelen sıçramaların sayısını temsil eder tve buna yenileme süreci denir.

Yorumlama

Rastgele zamanlarda meydana gelen olayları düşünürseniz, bekletme sürelerini düşünmeyi tercih edebilirsiniz. ${ displaystyle {S_ {i}: i geq 1 }}$ iki ardışık olay arasında geçen rastgele zaman olarak. Örneğin, yenileme süreci farklı makinelerin arıza sayılarını modelliyorsa, tutma süresi, bir makinenin diğerinden önce arızalanması arasındaki süreyi temsil eder.

Poisson süreci, benzersiz yenileme sürecidir. Markov özelliği,^[1] üstel dağılım, hafızasızlık özelliğine sahip benzersiz sürekli rastgele değişkendir.

Yenileme-ödüllendirme süreçleri

Yenileme-ödül sürecinin örnek evrimi ile tutma süreleri S_ben, zıplama zamanları J_n ve ödüller W_ben

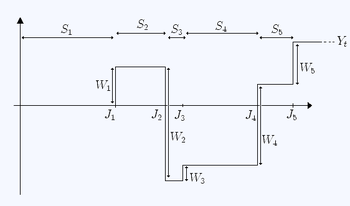
İzin Vermek ${ displaystyle W_ {1}, W_ {2}, ldots}$ dizisi olmak IID rastgele değişkenler (ödüller) doyurucu

${ displaystyle operatorname {E} | W_ {i} | < infty. ,}$

Sonra rastgele değişken

${ displaystyle Y_ {t} = toplam _ {i = 1} ^ {X_ {t}} W_ {i}}$

denir yenileme-ödül süreci. Unutmayın ki ${ displaystyle S_ {i}}$, her biri ${ displaystyle W_ {i}}$ pozitif değerlerin yanı sıra negatif değerler de alabilir.

Rastgele değişken ${ displaystyle Y_ {t}}$ iki sıraya bağlıdır: tutma süreleri ${ displaystyle S_ {1}, S_ {2}, ldots}$ ve ödüller${ displaystyle W_ {1}, W_ {2}, ldots}$ Bu iki dizinin bağımsız olması gerekmez. Özellikle, ${ displaystyle W_ {i}}$ bir işlevi olabilir ${ displaystyle S_ {i}}$.

Yorumlama

Tutma sürelerinin bir makinenin birbirini takip eden arızaları arasındaki zaman olarak yukarıdaki yorumu bağlamında, "ödüller" ${ displaystyle W_ {1}, W_ {2}, ldots}$ (bu durumda negatif olan), birbirini izleyen arızaların bir sonucu olarak ortaya çıkan ardışık onarım maliyetleri olarak görülebilir.

Alternatif bir benzetme, aralıklarla (bekletme süreleri) yumurta bırakan sihirli bir kazımız olmasıdır. ${ displaystyle S_ {i}}$. Bazen rastgele ağırlıkta altın yumurtalar bırakır ve bazen sorumlu (ve maliyetli) imha gerektiren toksik yumurtalar (ayrıca rastgele ağırlıkta) bırakır. "Ödüller" ${ displaystyle W_ {i}}$ birbirini izleyen yumurtalardan kaynaklanan ardışık (rastgele) mali kayıplar / kazançlardır (ben = 1,2,3, ...) ve ${ displaystyle Y_ {t}}$ o andaki toplam mali "ödülü" kaydeder t.

Yenileme işlevi

Biz tanımlıyoruz yenileme işlevi olarak beklenen değer bir zamana kadar gözlenen sıçrama sayısının ${ displaystyle t}$:

${ displaystyle m (t) = operatöradı {E} [X_ {t}]. ,}$

Temel yenileme teoremi

Yenileme işlevi tatmin eder

${ displaystyle lim _ {t ila infty} { frac {1} {t}} m (t) = { frac {1} { operatöradı {E} [S_ {1}]}}.}$

Kanıt

yenileme süreçleri için büyük sayıların güçlü kanunu ima eder ${ displaystyle lim _ {t ila infty} { frac {X_ {t}} {t}} = { frac {1} { operatöradı {E} [S_ {1}]}}.}$ Temel yenileme teoremini kanıtlamak için şunu göstermek yeterlidir: ${ displaystyle sol {{ frac {X_ {t}} {t}}; t geq 0 sağ }}$ düzgün bir şekilde entegre edilebilir. Bunu yapmak için, bekletme sürelerinin aşağıdakiler tarafından tanımlandığı bazı kısaltılmış yenileme sürecini düşünün. ${ displaystyle { overline {S_ {n}}} = a operatör adı { mathbb {I}} {S_ {n}> a }}$ nerede ${ displaystyle a}$ öyle bir noktadır ki ${ displaystyle 0$ tüm deterministik olmayan yenileme süreçleri için var olan. Bu yeni yenileme süreci ${ displaystyle { overline {X}} _ {t}}$ üst sınırdır ${ displaystyle X_ {t}}$ ve yenilenmeleri yalnızca kafes üzerinde gerçekleşebilir ${ displaystyle {na; n in mathbb {N} }}$. Ayrıca, her seferinde yenileme sayısı parametre ile geometriktir. ${ displaystyle p}$. Böylece sahibiz ${ displaystyle { begin {align} { overline {X_ {t}}} & leq sum _ {i = 1} ^ {[at]} operatorname {Geometric} (p) operatorname {E } left [, { overline {X_ {t}}} ^ {2} , right] & leq C_ {1} t + C_ {2} t ^ {2} P left ({ frac {X_ {t}} {t}}> x sağ) & leq { frac { operatöradı {E} sol [X_ {t} ^ {2} sağ]} {t ^ {2} x ^ {2}}} leq { frac { operatöradı {E} sol [{ overline {X_ {t}}} ^ {2} sağ]} {t ^ {2} x ^ {2} }} leq { frac {C} {x ^ {2}}}. end {hizalı}}}$

Yenileme ödül süreçleri için temel yenileme teoremi

Biz tanımlıyoruz ödül işlevi:

${ displaystyle g (t) = operatöradı {E} [Y_ {t}]. ,}$

Ödül işlevi tatmin eder

${ displaystyle lim _ {t ila infty} { frac {1} {t}} g (t) = { frac { operatöradı {E} [W_ {1}]} { operatöradı {E} [S_ {1}]}}.}$

Yenileme denklemi

Yenileme işlevi tatmin eder

${ displaystyle m (t) = F_ {S} (t) + int _ {0} ^ {t} m (t-s) f_ {S} (s) , ds}$

nerede ${ displaystyle F_ {S}}$ kümülatif dağılım işlevi ${ displaystyle S_ {1}}$ ve ${ displaystyle f_ {S}}$ karşılık gelen olasılık yoğunluk fonksiyonudur.

Kanıt[2]

İlk bekletme süresiyle ilgili beklentiyi yineleyebiliriz: ${ displaystyle m (t) = operatöradı {E} [X_ {t}] = operatöradı {E} [ operatöradı {E} (X_ {t} orta S_ {1})]. ,}$ Yenileme sürecinin tanımından, elimizde ${ displaystyle operatorname {E} (X_ {t} mid S_ {1} = s) = operatorname { mathbb {I}} _ { {t geq s }} left (1+ operatorname {E} [X_ {ts}] sağ). ,}$ Yani ${ displaystyle { begin {align} m (t) & = operatorname {E} [X_ {t}] [12pt] & = operatorname {E} [ operatorname {E} (X_ {t} orta S_ {1})] [12pt] & = int _ {0} ^ { infty} operatöradı {E} (X_ {t} mid S_ {1} = s) f_ {S} (s ) , ds [12pt] & = int _ {0} ^ { infty} operatorname { mathbb {I}} _ { {t geq s }} left (1+ operatorname { E} [X_ {ts}] sağ) f_ {S} (s) , ds [12pt] & = int _ {0} ^ {t} left (1 + m (ts) sağ) f_ {S} (s) , ds [12pt] & = F_ {S} (t) + int _ {0} ^ {t} m (ts) f_ {S} (s) , ds, end {hizalı}}}$ gereğince, gerektiği gibi.

Anahtar yenileme teoremi

İzin Vermek X yenileme işlevi olan bir yenileme süreci olmak ${ displaystyle m (t)}$ ve yenilenme arası ortalama ${ displaystyle mu}$. İzin Vermek ${ displaystyle g: [0, infty) rightarrow [0, infty)}$ tatmin edici bir işlev olun:

• ${ displaystyle int _ {0} ^ { infty} g (t) , dt < infty}$
• g monotondur ve artmaz

Anahtar yenileme teoremi şunu belirtir: ${ displaystyle t rightarrow infty}$:^[3]

${ displaystyle int _ {0} ^ {t} g (tx) m '(x) , dx rightarrow { frac {1} { mu}} int _ {0} ^ { infty} g (x) , dx}$

Yenileme teoremi

Düşünen ${ displaystyle g (x) = mathbb {I} _ {[0, h]} (x)}$ herhangi ${ displaystyle h> 0}$ özel bir durum olarak yenileme teoremini verir:^[4]

${ Displaystyle m (t + h) -m (t) sağ { frac {h} { mu}}}$ gibi ${ displaystyle t rightarrow infty}$

Sonuç, integral denklemler kullanılarak veya bir bağlantı argüman.^[5] Anahtar yenileme teoreminin özel bir durumu olsa da, adım fonksiyonlarını göz önünde bulundurarak ve ardından adım fonksiyonlarının sıralarını artırarak tam teoremi çıkarmak için kullanılabilir.^[3]

Asimptotik özellikler

Yenileme süreçleri ve yenileme-ödül süreçleri, aşağıdakilere benzer özelliklere sahiptir: büyük sayıların güçlü kanunu, aynı teoremden türetilebilir. Eğer ${ displaystyle (X_ {t}) _ {t geq 0}}$ bir yenileme sürecidir ve ${ displaystyle (Y_ {t}) _ {t geq 0}}$ bir yenileme ödül sürecidir, bu durumda:

${ displaystyle lim _ {t ila infty} { frac {1} {t}} X_ {t} = { frac {1} { operatöradı {E} [S_ {1}]}}}$^[6]

${ displaystyle lim _ {t ila infty} { frac {1} {t}} Y_ {t} = { frac {1} { operatöradı {E} [S_ {1}]}} operatör adı {E} [W_ {1}]}$

neredeyse kesin.

Kanıt

Önce düşünün ${ displaystyle (X_ {t}) _ {t geq 0}}$. Tanım gereği elimizde: ${ displaystyle J_ {X_ {t}} leq t leq J_ {X_ {t} +1}}$ hepsi için ${ displaystyle t geq 0}$ ve bu yüzden ${ displaystyle { frac {J_ {X_ {t}}} {X_ {t}}} leq { frac {t} {X_ {t}}} leq { frac {J_ {X_ {t} + 1}} {X_ {t}}}}$ hepsi için t ≥ 0. Şimdi beri ${ displaystyle 0 < operatöradı {E} [S_ {i}] < infty}$ sahibiz: ${ displaystyle X_ {t} ila infty}$ gibi ${ displaystyle t ila infty}$ neredeyse kesin (1 olasılıkla). Dolayısıyla: ${ displaystyle { frac {J_ {X_ {t}}} {X_ {t}}} = { frac {J_ {n}} {n}} = { frac {1} {n}} toplam _ {i = 1} ^ {n} S_ {i} - operatöradı {E} [S_ {1}]}$ neredeyse kesin olarak (büyük sayıların güçlü yasasını kullanarak); benzer şekilde: ${ displaystyle { frac {J_ {X_ {t} +1}} {X_ {t}}} = { frac {J_ {X_ {t} +1}} {X_ {t} +1}} { frac {X_ {t} +1} {X_ {t}}} = { frac {J_ {n + 1}} {n + 1}} { frac {n + 1} {n}} to operatorname {E} [S_ {1}] cdot 1}$ neredeyse kesin. Böylece (beri ${ displaystyle t / X_ {t}}$ iki terim arasında sıkıştırılır) ${ displaystyle { frac {1} {t}} X_ {t} - { frac {1} { operatorname {E} [S_ {1}]}}}$ neredeyse kesin.[3] Sonra düşünün ${ displaystyle (Y_ {t}) _ {t geq 0}}$. Sahibiz ${ displaystyle { frac {1} {t}} Y_ {t} = { frac {X_ {t}} {t}} { frac {1} {X_ {t}}} Y_ {t} { frac {1} { operatöradı {E} [S_ {1}]}} cdot operatöradı {E} [W_ {1}]}$ neredeyse kesin olarak (ilk sonucu kullanarak ve büyük sayılar yasasını kullanarak ${ displaystyle Y_ {t}}$).

Yenileme süreçleri ayrıca aşağıdakilere benzer bir özelliğe sahiptir: Merkezi Limit Teoremi:^[6]

${ displaystyle { frac {X_ {t} -t / mu} { sqrt {t sigma ^ {2} / mu ^ {3}}}}}$

Denetim paradoksu

Rastgele nokta tarafından belirlenen yenileme aralığı t (kırmızıyla gösterilmiştir) stokastik olarak ilk yenileme aralığından daha büyüktür.

Yenileme süreçlerinin ilginç bir özelliği, önceden belirlenmiş bir süre beklersek t ve sonra yenileme aralığının ne kadar geniş olduğunu gözlemleyin. t , tipik olarak ortalama büyüklükteki bir yenileme aralığından daha büyük olmasını beklemeliyiz.

Matematiksel olarak denetim paradoksu şunu belirtir: herhangi bir t> 0 için t içeren yenileme aralığı stokastik olarak daha büyük ilk yenileme aralığından daha fazla. Yani herkes için x > 0 ve hepsi için t > 0:

${ displaystyle operatorname {P} (S_ {X_ {t} +1}> x) geq operatorname {P} (S_ {1}> x) = 1-F_ {S} (x)}$

nerede F_S IID bekletme sürelerinin kümülatif dağılım fonksiyonudur S_ben.

Paradoksun çözümü, zaman zaman örneklenmiş dağıtımımızın t boyuta bağlıdır, çünkü bir aralığın seçilme olasılığı boyutuyla orantılıdır. Bununla birlikte, ortalama büyüklükte bir yenileme aralığı, boyuta bağlı değildir.

Kanıt

Önceki son atlama süresinin t dır-dir ${ displaystyle J_ {X_ {t}}}$; ve yenileme aralığı şunları içerir: t dır-dir ${ displaystyle S_ {X_ {t} +1}}$. Sonra ${ displaystyle { begin {align} operatorname {P} (S_ {X_ {t} +1}> x) & {} = int _ {0} ^ { infty} operatorname {P} (S_ { X_ {t} +1}> x mid J_ {X_ {t}} = s) f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ { 0} ^ { infty} operatöradı {P} (S_ {X_ {t} +1}> x | S_ {X_ {t} +1}> ts) f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} { frac { operatöradı {P} (S_ {X_ {t} +1}> x ,, , S_ {X_ {t} +1}> ts)} { operatöradı {P} (S_ {X_ {t} +1}> ts)}} f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} { frac {1-F ( max {x, ts })} {1-F (ts)}} f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} min left {{ frac {1-F (x)} {1-F (ts)}}, { frac {1-F (ts)} {1-F (ts)}} sağ } f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} min left {{ frac {1-F (x)} {1-F (ts)}}, 1 sağ } f_ {J_ {X_ {t}}} (s) , ds [12pt] ve {} geq int _ {0} ^ { infty} (1-F (x)) f_ {J_ {X_ {t}}} (s) , ds = 1-F (x) = operatöradı {P} (S_ {1}> x), [12pt] end {hizalı}}}$ ikisinden beri ${ displaystyle { frac {1-F (x)} {1-F (t-s)}}}$ ve ${ displaystyle 1}$ büyük veya eşittir ${ displaystyle 1-F (x)}$ tüm değerleri için s.

Süperpozisyon

Yenileme süreci bir Poisson süreci olmadığı sürece, iki bağımsız yenileme sürecinin üst üste binmesi (toplamı) bir yenileme süreci değildir.^[7] Bununla birlikte, bu tür süreçler, adı verilen daha geniş bir süreç sınıfı içinde tanımlanabilir. Markov yenileme süreçleri.^[8] Ancak kümülatif dağılım fonksiyonu Süperpozisyon sürecindeki ilk olaylar arası sürenin^[9]

${ displaystyle R (t) = 1- toplamı _ {k = 1} ^ {K} { frac { alpha _ {k}} { toplamı _ {l = 1} ^ {K} alpha _ { l}}} (1-R_ {k} (t)) prod _ {j = 1, j neq k} ^ {K} alpha _ {j} int _ {t} ^ { infty} ( 1-R_ {j} (u)) , { text {d}} u}$

nerede R_k(t) ve α_k > 0, olaylar arası zamanların CDF'si ve sürecin geliş hızıdır k.^[10]

Örnek uygulama

Girişimci Eric'in n her biri sıfır ile iki yıl arasında eşit olarak dağıtılmış bir çalışma ömrüne sahip makineler. Eric, değiştirme maliyeti 2600 € ile arızalanana kadar her makinenin çalışmasına izin verebilir; alternatif olarak, 200 € 'luk bir maliyetle hala çalışır durumdayken herhangi bir zamanda bir makineyi değiştirebilir.

Optimum değiştirme politikası nedir?

Çözüm

Yaşam süresi n makineler şu şekilde modellenebilir: n bağımsız eşzamanlı yenileme-ödül süreçleri, bu nedenle davayı dikkate almak yeterlidir n = 1. Bu süreci şununla belirtin: ${ displaystyle (Y_ {t}) _ {t geq 0}}$. Ardışık yaşamlar S Değiştirilen makinelerin% 50'si bağımsızdır ve aynı şekilde dağıtılmıştır, bu nedenle optimum politika, süreçteki tüm yedek makineler için aynıdır. Eric bir makinenin ömrünün başında makineyi zamanında değiştirmeye karar verirse 0 < t < 2 ancak makine bu zamandan önce, sonra da ömür boyu başarısız olur S [0,t] ve dolayısıyla 0,5 beklentisine sahiptirt. Dolayısıyla, makinenin beklenen genel kullanım ömrü: ${ displaystyle { begin {align} operatorname {E} [S] & = operatorname {E} [S mid { text {daha önce başarısızdır}} t] cdot operatorname {P} [{ text { }} t] + operatöradı {E} [S mid { text {daha önce başarısız olmaz}} t] cdot operatöradı {P} [{ text {daha önce başarısız olmaz}} t] [6pt] & = 0,5t ({ frac {t} {2}}) + t ({ frac {2-t} {2}}) end {hizalı}}}$ ve beklenen maliyet W makine başına: ${ displaystyle { begin {align} operatorname {E} [W] & = operatorname {E} [W mid { text {daha önce başarısız olur}} t] cdot operatorname {P} ({ text { önce başarısız olur}} t) + operatorname {E} [W mid { text {daha önce başarısız olmaz}} t] cdot operatorname {P} ({ text {daha önce başarısız olmaz}} t) [6pt] & = 2600 ({ frac {t} {2}}) + 200 ({ frac {2-t} {2}}) = 1200t + 200. End {hizalı}}}$ Dolayısıyla, büyük sayıların güçlü yasasına göre, uzun vadeli ortalama birim zaman maliyeti: ${ displaystyle { frac {1} {t}} Y_ {t} simeq { frac { operatöradı {E} [W]} { operatöradı {E} [S]}} = { frac {4 ( 1200t + 200)} {t ^ {2} + 4t-2t ^ {2}}}}$ sonra göre farklılaşmak t: ${ displaystyle { frac { kısmi} { kısmi t}} { frac {4 (1200t + 200)} {t ^ {2} + 4t-2t ^ {2}}} = 4 { frac {( 4t-t ^ {2}) (1200) - (4-2t) (1200t + 200)} {(t ^ {2} + 4t-2t ^ {2}) ^ {2}}},}$ bu, dönüm noktalarının şunları sağladığını gösterir: ${ displaystyle { begin {align} 0 & = (4t-t ^ {2}) (1200) - (4-2t) (1200t + 200) = 4800t-1200t ^ {2} -4800t-800 + 2400t ^ { 2} + 400t [6pt] & = - 800 + 400t + 1200t ^ {2}, end {hizalı}}}$ ve böylece ${ displaystyle 0 = 3t ^ {2} + t-2 = (3t-2) (t + 1).}$ Tek çözümü alıyoruz t [0, 2] içinde: t = 2/3. Bu aslında minimumdur (ve maksimum değildir), çünkü birim zaman başına maliyet sonsuza t sıfıra meyillidir, yani maliyet azaldıkça t artmaya başladığı 2/3 noktasına kadar artar.

Ayrıca bakınız

• Campbell teoremi (olasılık)
• Bileşik Poisson süreci
• Sürekli zamanlı Markov süreci
• Little lemma
• Palm-Khintchine teoremi
• Poisson süreci
• Kuyruk teorisi
• Artık zaman
• Harabe teorisi
• Yarı Markov süreci

Bu makale genel bir liste içerir Referanslar, ancak büyük ölçüde doğrulanmamış kalır çünkü yeterli karşılık gelmiyor satır içi alıntılar. Lütfen yardım edin geliştirmek bu makale tanıtım daha kesin alıntılar. (Temmuz 2010) (Bu şablon mesajını nasıl ve ne zaman kaldıracağınızı öğrenin)

Notlar

Referanslar

• Cox, David (1970). Yenileme Teorisi. Londra: Methuen & Co. s. 142. ISBN  0-412-20570-X.
• Doob, J.L. (1948). "Olasılık Teorisi Açısından Yenileme Teorisi" (PDF). Amerikan Matematik Derneği İşlemleri. 63 (3): 422–438. doi:10.2307/1990567. JSTOR  1990567.
• Feller, William (1971). Olasılık teorisine ve uygulamalarına giriş. 2 (ikinci baskı). Wiley.
• Grimmett, G.R.; Stirzaker, D.R. (1992). Olasılık ve Rastgele Süreçler (ikinci baskı). Oxford University Press. ISBN  0198572220.
• Smith, Walter L. (1958). "Yenileme Teorisi ve Sonuçları". Kraliyet İstatistik Derneği Dergisi, Seri B. 20 (2): 243–302. JSTOR  2983891.
• Wanli Wang, Johannes H.P. Schulz, Weihua Deng ve Eli Barkai (2018). "Yağ kuyruklu dağınık kalma süreleri ile yenileme teorisi: Tipik ve nadir". Phys. Rev. E. 98 (4): 042139. arXiv:1809.05856. Bibcode:2018PhRvE..98d2139W. doi:10.1103 / PhysRevE.98.042139.