Harmonik seriler (matematik) - Harmonic series (mathematics)

İçinde matematik, harmonik seriler ... farklı sonsuz seriler

${ displaystyle toplamı _ {n = 1} ^ { infty} { frac {1} {n}} = 1 + { frac {1} {2}} + { frac {1} {3}} + { frac {1} {4}} + { frac {1} {5}} + cdots.}$

Adı kavramından türemiştir. armoniler veya harmonikler müziğin içinde: dalga boyları titreşen bir telin armonilerinden 1/2, 1/3, 1/4vb., dizenin temel dalga boyu. Serinin ilkinden sonraki her dönemi harmonik ortalama komşu terimler; ifade harmonik ortalama aynı şekilde müzikten türemiştir.

Tarih

Harmonik serinin farklılığı ilk olarak 14. yüzyılda kanıtlanmıştır. Nicole Oresme,^[1] ancak bu başarı belirsizliğe düştü. 17. yüzyılda kanıtlar Pietro Mengoli^[2] ve tarafından Johann Bernoulli,^[3]erkek kardeşi tarafından yayınlanan ve popüler hale getirilen ikinci kanıt Jacob Bernoulli.^[4][5]

Tarihsel olarak, armonik diziler mimarlar arasında belli bir popülerliğe sahipti. Bu özellikle Barok mimarların bunları inşa etmek için kullandıkları dönem oranlar nın-nin kat planları, nın-nin yükselmeler kilise ve sarayların hem iç hem de dış mimari detayları arasında uyumlu ilişkiler kurmak.^[6]

uyuşmazlık

Harmonik serilerin ıraksamasının iyi bilinen birkaç kanıtı vardır. Bunlardan birkaçı aşağıda verilmiştir.

Karşılaştırma testi

Sapmayı kanıtlamanın bir yolu, harmonik seriyi başka bir ıraksak seriyle karşılaştırmaktır; burada her payda bir sonraki en büyük ile değiştirilir. ikinin gücü:

${ displaystyle { begin {alignat} {8} 1 & + { frac {1} {2}} && + { frac {1} {3}} && + { frac {1} {4}} && + { frac {1} {5}} && + { frac {1} {6}} && + { frac {1} {7}} && + { frac {1} {8}} && + { frac {1} {9}} && + cdots [5pt] {} geq 1 & + { frac {1} {2}} && + { frac {1} { color {kırmızı} { mathbf {4}}}} && + { frac {1} {4}} && + { frac {1} { color {red} { mathbf {8}}}} && + { frac {1} { color {kırmızı} { mathbf {8}}}} && + { frac {1} { color {red} { mathbf {8}}}} && + { frac {1} {8}} && + { frac {1} { color {red} { mathbf {16}}}} && + cdots end {alignat}}}$

Harmonik serinin her bir terimi, ikinci serinin karşılık gelen teriminden daha büyük veya ona eşittir ve bu nedenle, harmonik serinin toplamı, ikinci serinin toplamından büyük veya ona eşit olmalıdır. Bununla birlikte, ikinci dizinin toplamı sonsuzdur:

${ displaystyle { begin {align} & 1 + left ({ frac {1} {2}} sağ) + left ({ frac {1} {4}} + { frac {1} {4} } right) + left ({ frac {1} {8}} + { frac {1} {8}} + { frac {1} {8}} + { frac {1} {8} } right) + left ({ frac {1} {16}} + cdots + { frac {1} {16}} right) + cdots [5pt] {} = {} & 1+ { frac {1} {2}} + { frac {1} {2}} + { frac {1} {2}} + { frac {1} {2}} + cdots = infty. son {hizalı}}}$

Takip eder (tarafından karşılaştırma testi ) harmonik serilerin toplamının da sonsuz olması gerekir. Daha doğrusu, yukarıdaki karşılaştırma şunu kanıtlıyor:

${ displaystyle toplamı _ {n = 1} ^ {2 ^ {k}} { frac {1} {n}} geq 1 + { frac {k} {2}}}$

her biri için pozitif tamsayı k.

Bu kanıt, öneren Nicole Oresme 1350 civarında, matematik camiasındaki birçok kişi tarafından kabul edilir^{[Kim tarafından? ]} zirvede olmak ortaçağ matematiği. Hala bugün matematik derslerinde öğretilen standart bir kanıttır. Cauchy'nin yoğunlaşma testi bu argümanın bir genellemesidir.

İntegral testi

İntegral testinin çizimi.

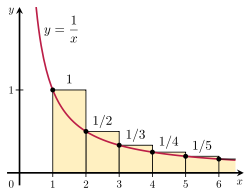
Harmonik serinin toplamını bir ile karşılaştırarak ıraksadığını ispatlamak mümkündür. uygunsuz integral. Özellikle, sağdaki şekilde gösterilen dikdörtgenlerin düzenini göz önünde bulundurun. Her dikdörtgen 1 birim genişliğinde ve 1/n birimler yüksek olduğundan, sonsuz sayıda dikdörtgenin toplam alanı harmonik serilerinin toplamıdır:

${ displaystyle { begin {dizi} {c} { text {alan}} { text {rectangles}} end {array}} = 1 + { frac {1} {2}} + { frac {1} {3}} + { frac {1} {4}} + { frac {1} {5}} + cdots}$

Ek olarak, eğrinin altındaki toplam alan y = 1/x 1'den sonsuza bir ıraksak ile verilir uygunsuz integral:

${ displaystyle { begin {dizi} {c} { text {altındaki alan}} { text {curve}} end {dizi}} = int _ {1} ^ { infty} { frac {1} {x}} , dx = infty.}$

Bu alan tamamen dikdörtgenlerin içinde olduğundan, dikdörtgenlerin toplam alanı da sonsuz olmalıdır. Daha doğrusu, bu kanıtlıyor

${ displaystyle toplamı _ {n = 1} ^ {k} { frac {1} {n}}> int _ {1} ^ {k + 1} { frac {1} {x}} , dx = ln (k + 1).}$

Bu argümanın genelleştirilmesi, integral testi.

Iraksama oranı

Harmonik seri çok yavaş uzaklaşır. Örneğin, ilk 10'un toplamı⁴³ terim 100'den az.^[7] Bunun nedeni serinin kısmi toplamlarının logaritmik büyüme. Özellikle,

${ displaystyle toplamı _ {n = 1} ^ {k} { frac {1} {n}} = ln k + gamma + varepsilon _ {k} leq ( ln k) +1}$

nerede γ ... Euler – Mascheroni sabiti ve ε_k ~ 1/2k 0'a yaklaşan k sonsuza gider. Leonhard Euler hem bunu hem de daha çarpıcı gerçeği kanıtladı, sadece asalların karşılıklıları ayrıca farklılaşır, yani

${ displaystyle sum _ {p { text {prime}}} { frac {1} {p}} = { frac {1} {2}} + { frac {1} {3}} + { frac {1} {5}} + { frac {1} {7}} + { frac {1} {11}} + { frac {1} {13}} + { frac {1} { 17}} + cdots = infty.}$

Kısmi meblağlar

Uzaklaşan harmonik serilerin sonlu kısmi toplamları,

${ displaystyle H_ {n} = toplam _ {k = 1} ^ {n} { frac {1} {k}},}$

arandı harmonik sayılar.

Arasındaki fark H_n ve ln n yakınsamak Euler – Mascheroni sabiti. Herhangi iki harmonik sayı arasındaki fark asla bir tam sayı değildir. Hariç hiçbir harmonik sayı tam sayı değildir. H₁ = 1.^{[8]:s. 24[9]:Thm. 1}

İlgili seriler

Alternatif harmonik seriler

Değişen harmonik serinin (siyah çizgi bölümleri) ilk on dört kısmi toplamı, 2'nin (kırmızı çizgi) doğal logaritmasına yakınsadığı gösterilmiştir.

Seri

${ displaystyle sum _ {n = 1} ^ { infty} { frac {(-1) ^ {n + 1}} {n}} = 1 - { frac {1} {2}} + { frac {1} {3}} - { frac {1} {4}} + { frac {1} {5}} - cdots}$

olarak bilinir alternatif harmonik seriler. Bu seri, alternatif seri testi. Özellikle, toplam şuna eşittir: 2'nin doğal logaritması:

${ displaystyle 1 - { frac {1} {2}} + { frac {1} {3}} - { frac {1} {4}} + { frac {1} {5}} - cdots = ln 2.}$

Alternatif harmonik serisi, koşullu yakınsak, değil kesinlikle yakınsak: Serideki terimler sistematik olarak yeniden düzenlenirse, genel olarak toplam farklı olur ve yeniden düzenlemeye bağlı olarak muhtemelen sonsuz olur.

Alternatif harmonik seri formülü, özel bir durumdur. Mercator serisi, Taylor serisi doğal logaritma için.

İlgili bir seri, Taylor serisinden türetilebilir. arktanjant:

${ displaystyle toplamı _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {2n + 1}} = 1 - { frac {1} {3}} + { frac {1} {5}} - { frac {1} {7}} + cdots = { frac { pi} {4}}.}$

Bu, Leibniz serisi.

Genel harmonik seriler

genel harmonik seriler formda

${ displaystyle toplamı _ {n = 0} ^ { infty} { frac {1} {an + b}},}$

nerede a ≠ 0 ve b gerçek sayılardır ve b/a sıfır veya negatif bir tam sayı değildir.

Harmonik serilerle limit karşılaştırma testi ile, tüm genel harmonik serileri de ayrılmaktadır.

p-dizi

Harmonik serinin bir genellemesi, p-dizi (veya hyperharmonic serisi) olarak tanımlanır

${ displaystyle toplamı _ {n = 1} ^ { infty} { frac {1} {n ^ {p}}}}$

herhangi bir gerçek sayı için p. Ne zaman p = 1, p-seri, ıraksayan harmonik seridir. Ya integral testi ya da Cauchy yoğunlaşma testi gösterir ki p-serisi herkes için birleşir p > 1 (bu durumda buna aşırı harmonik seriler) ve herkes için farklılaşır p ≤ 1. Eğer p > 1 sonra toplamı p-seri ζ(p)yani Riemann zeta işlevi değerlendirildi p.

Toplamı bulma sorunu p = 2 denir Basel sorunu; Leonhard Euler gösterdi π²/6. Toplamın değeri p = 3 denir Apéry sabiti, dan beri Roger Apéry bunun bir olduğunu kanıtladı irrasyonel sayı.

ln serisi

İlişkili p-dizi ... ln serisi, olarak tanımlandı

${ displaystyle toplamı _ {n = 2} ^ { infty} { frac {1} {n ( ln n) ^ {p}}}}$

herhangi bir pozitif gerçek sayı için p. Bu, ayrılmak için integral testi ile gösterilebilir. p ≤ 1 ama hepsi için birleş p > 1.

φ-dizi

Herhangi dışbükey, gerçek değerli işlev φ öyle ki

${ displaystyle limsup _ {u to 0 ^ {+}} { frac { varphi left ({ frac {u} {2}} sağ)} { varphi (u)}} <{ frac {1} {2}},}$

seri

${ displaystyle toplamı _ {n = 1} ^ { infty} varphi sol ({ frac {1} {n}} sağ)}$

yakınsaktır.^{[kaynak belirtilmeli ]}

Rastgele harmonik seriler

Rastgele harmonik serisi

${ displaystyle toplamı _ {n = 1} ^ { infty} { frac {s_ {n}} {n}},}$

nerede s_n vardır bağımsız eşit olarak +1 ve −1 değerlerini alan aynı şekilde dağıtılmış rastgele değişkenler olasılık 1/2, yakınsayan bir dizi rastgele değişken için olasılık teorisinde iyi bilinen bir örnektir olasılıkla 1. Bu yakınsamanın gerçeği, her ikisinin de kolay bir sonucudur. Kolmogorov üç serili teoremi veya yakından ilgili Kolmogorov maksimal eşitsizliği. Alberta Üniversitesi'nden Byron Schmuland daha fazla inceledi^[10] rastgele harmonik serilerinin özellikleri ve yakınsak serilerin bir rastgele değişken bazı ilginç özelliklere sahip. Özellikle, olasılık yoğunluk fonksiyonu +2'de veya −2'de değerlendirilen bu rastgele değişkenin değeri, 0.124999999999999999999999999999999999999999764..., farklı olarak 1/8 10'dan az⁻⁴². Schmuland'ın makalesi, bu olasılığın neden bu kadar yakın olduğunu, ancak tam olarak değil, 1/8. Bu olasılığın tam değeri, sonsuz kosinüs çarpım integrali ile verilir. C₂^[11] bölü π.

Tükenmiş harmonik seriler

Paydanın herhangi bir yerinde 9 rakamının göründüğü tüm terimlerin kaldırıldığı tükenmiş harmonik serisinin değere yakınsadığı gösterilebilir. 22.92067661926415034816....^[12] Aslında, belirli bir rakam dizisini içeren tüm terimler (herhangi bir temel ) kaldırılırsa seri birleşir.^[13]

Başvurular

Harmonik seri olabilir mantıksız onunla ilk karşılaşan öğrencilere, çünkü bu bir ıraksak seriler sınırı olsa bile nterim olarak n sonsuza gider sıfırdır. Harmonik serinin ıraksaması aynı zamanda bazı belirgin paradokslar. Bunlara bir örnek "lastik bantta solucan ".^[14] Bir solucanın, lastik bant düzgün bir şekilde gerilirken aynı zamanda sonsuz elastik bir metrelik lastik bant boyunca süründüğünü varsayalım. Solucan dakikada 1 santimetre hareket ederse ve bant dakikada 1 metre uzarsa, solucan lastik bandın sonuna ulaşır mı? Yanıt, sezgiye aykırı bir şekilde, "evet" dir. n dakika, solucanın kat ettiği mesafenin lastik bandın toplam uzunluğuna oranı

${ displaystyle { frac {1} {100}} sum _ {k = 1} ^ {n} { frac {1} {k}}.}$

(Aslında bant sürekli genişlediğinden gerçek oran bu toplamdan biraz daha azdır.)

Çünkü dizi keyfi olarak büyüyor n daha büyük hale gelir, sonunda bu oran 1'i geçmelidir, bu da solucanın lastik bandın sonuna ulaştığı anlamına gelir. Ancak, değeri n bunun meydana geldiği yer son derece büyük olmalıdır: yaklaşık e¹⁰⁰, 10'u aşan bir sayı⁴³ dakika (10³⁷ yıl). Harmonik seriler birbirinden uzaklaşsa da, bunu çok yavaş yapar.

Harmonik seriyi ilgilendiren bir diğer problem ise Jeep sorunu, hangisi (bir biçimde), ne kadar toplam yakıt gerektiğini sorar. cip Çölü geçmek için sınırlı yakıt taşıma kapasitesi olan ve muhtemelen rota boyunca yakıt damlaları bırakan. Belirli bir yakıt miktarı ile katedilebilecek mesafe, logaritmik olarak büyüyen harmonik serilerinin kısmi toplamları ile ilgilidir. Ve böylece gerekli yakıt istenen mesafe ile katlanarak artar.

blok yığınlama sorunu: harmonik serisine göre hizalanmış bloklar, herhangi bir genişlikteki bölünmeleri köprüler.

Başka bir örnek de blok yığınlama sorunu: özdeş dominolardan oluşan bir koleksiyon verildiğinde, onları masanın kenarına düşmeden sarkacak şekilde masanın kenarına dizmek açıkça mümkündür. Mantıksız sonuç, yeterince domino olması koşuluyla, çıkıntıyı keyfi olarak büyük yapacak şekilde istiflenebilmesidir.^[14][15]

Daha basit bir örnek ise havuzun duvarlarına dokunurken daha fazla hız eklemeye devam eden yüzücüdür. Yüzücü 10 metrelik bir havuzu 2 m / s hızla geçmeye başlar ve her çaprazlamada hıza 2 m / s daha eklenir. Teorik olarak, yüzücünün hızı sınırsızdır, ancak bu hıza ulaşmak için gereken havuz geçişlerinin sayısı çok büyük hale gelir; örneğin, ulaşmak için ışık hızı (görmezden gelerek Özel görelilik ), yüzücünün havuzu 150 milyon kez geçmesi gerekir. Bu büyük sayının aksine, belirli bir hıza ulaşmak için gereken süre, herhangi bir sayıdaki havuz geçişlerinde (yinelemeler) serilerin toplamına bağlıdır:

${ displaystyle { frac {10} {2}} sum _ {k = 1} ^ {n} { frac {1} {k}}.}$

Toplamı hesaplamak (yinelemeli olarak) ışık hızına ulaşmak için gereken sürenin yalnızca 97 saniye olduğunu gösterir. Bu noktanın ötesine geçerek (ışık hızını aşarak, yine görmezden gelerek) Özel görelilik ), havuzu geçmek için geçen süre aslında yinelemelerin sayısı çok büyük hale geldikçe sıfıra yaklaşacaktır ve havuzu geçmek için gereken süre sıfır gibi görünse de (sonsuz sayıda yinelemede), yinelemelerin toplamı (toplam havuz geçişleri için geçen süre) yine de çok yavaş bir hızda sapacaktır.

Ayrıca bakınız

• Dirichlet eta işlevi
• Harmonik ilerleme
• Karşılıklı toplamların listesi

Referanslar

Dış bağlantılar

• "Harmonik seriler", Matematik Ansiklopedisi, EMS Basın, 2001 [1994]
• "Harmonik Seriler Tekrar Tekrar Ayrılıyor" (PDF). AMATYC İncelemesi. 27: 31–43. 2006.
• Weisstein, Eric W. "Harmonik Seriler". MathWorld.
• Weisstein, Eric W. "Kitap İstifleme Sorunu". MathWorld.
• Hudelson, Matt (1 Ekim 2010). "Sözcük Olmadan İspat: Alternatif Harmonik Seriler Toplamları ln 2'ye Kadar" (PDF). Matematik Dergisi. 83 (4): 294. doi:10.4169 / 002557010X521831. S2CID  119484945.