Rössler çekicisi - Rössler attractor

Rössler çekicisi

Rössler çekicisi olarak stereogram ile

{ displaystyle a = 0.2}

,

{ displaystyle b = 0.2}

,

{ displaystyle c = 14}

Rössler çekicisi /ˈrɒslər/ ... cazibe merkezi için Rössler sistemi, üç sistem doğrusal olmayan adi diferansiyel denklemler başlangıçta tarafından incelendi Otto Rössler.^[1]^[2] Bu diferansiyel denklemler bir sürekli zamanlı dinamik sistem o sergiler kaotik ile ilişkili dinamikler fraktal çekicinin özellikleri.^[3]

Rössler sisteminin bazı özellikleri aşağıdaki gibi doğrusal yöntemlerle çıkarılabilir: özvektörler, ancak sistemin ana özellikleri gibi doğrusal olmayan yöntemler gerektirir Poincaré haritaları ve çatallanma diyagramları. Orijinal Rössler makalesi, Rössler çekicisinin tıpkı şeye benzer şekilde davranması gerektiğini belirtir. Lorenz çekicisi aynı zamanda niteliksel olarak analiz etmek daha kolay olabilir.^[1] Bir yörünge çekicinin içinde, yakın bir dışa doğru spiral izler ${ displaystyle x, y}$ kararsız bir sabit nokta etrafında düzlem. Grafik yeterince dışa doğru döndüğünde, ikinci bir sabit nokta grafiği etkiler ve grafikte bir artış ve bükülmeye neden olur. ${ displaystyle z}$ boyut. Zaman alanında, her değişkenin sabit bir değerler aralığı içinde salınmasına rağmen, salınımların kaotik olduğu ortaya çıkar. Bu çekicinin Lorenz çekiciyle bazı benzerlikleri vardır, ancak daha basittir ve yalnızca bir manifold. Otto Rössler 1976'da Rössler çekicisini tasarladı,^[1] ancak orijinal teorik denklemlerin daha sonra kimyasal reaksiyonlarda dengeyi modellemede yararlı olduğu bulundu.

Tanım

Rössler sisteminin tanımlayıcı denklemleri:^[3]

${ displaystyle { begin {case} { frac {dx} {dt}} = - yz { frac {dy} {dt}} = x + ay { frac {dz} {dt}} = b + z (xc) end {vakalar}}}$

Rössler, kaotik çeker ile ${ displaystyle a = 0.2}$ , ${ displaystyle b = 0.2}$ , ve ${ displaystyle c = 5.7}$ ama özellikleri ${ displaystyle a = 0.1}$ , ${ displaystyle b = 0.1}$ , ve ${ displaystyle c = 14}$ o zamandan beri daha yaygın olarak kullanılmaktadır. Parametre uzayının başka bir çizgisi topolojik analiz kullanılarak incelenmiştir. Karşılık gelir ${ displaystyle b = 2}$ , ${ displaystyle c = 4}$ , ve ${ displaystyle a}$ çatallanma parametresi olarak seçilmiştir.^[4] Rössler bu denklem setini nasıl keşfetti Letellier ve Messager tarafından araştırıldı.^[5]

Bir analiz

{ displaystyle x, y}

ile Rössler çekicinin düzlemi

{ displaystyle a = 0.2}

,

{ displaystyle b = 0.2}

,

{ displaystyle c = 5.7}

Rössler çekicinin zarafetinin bir kısmı denklemlerinden ikisinin doğrusal olmasından kaynaklanıyor; ayar ${ displaystyle z = 0}$ , üzerindeki davranışın incelenmesini sağlar ${ displaystyle x, y}$ uçak

${ displaystyle { begin {case} { frac {dx} {dt}} = - y { frac {dy} {dt}} = x + ay end {case}}}$

İstikrar ${ displaystyle x, y}$ uçak daha sonra hesaplanarak bulunabilir özdeğerler of Jacobian ${ displaystyle { begin {pmatrix} 0 & -1 1 & a end {pmatrix}}}$ , hangileri ${ displaystyle (a pm { sqrt {a ^ {2} -4}}) / 2}$ . Bundan ne zaman olduğunu görebiliriz ${ displaystyle 0$ , özdeğerler karmaşıktır ve her ikisinin de pozitif bir gerçek bileşeni vardır, bu da orijini kararsız hale getirir. ${ displaystyle x, y}$ uçak. Şimdi düşünün ${ displaystyle z}$ için bu aralık bağlamında düzlem davranışı ${ displaystyle a}$ . Olduğu sürece ${ displaystyle x}$ den daha küçük ${ displaystyle c}$ , ${ displaystyle c}$ terim yörüngeyi yakın tutacak ${ displaystyle x, y}$ uçak. Yörünge yaklaşırken ${ displaystyle x}$ daha büyük ${ displaystyle c}$ , ${ displaystyle z}$ -değerler yükselmeye başlar. Gibi ${ displaystyle z}$ tırmanıyor olsa da ${ displaystyle -z}$ denkleminde ${ displaystyle dx / dt}$ büyümeyi durdurur ${ displaystyle x}$ .

Sabit noktalar

Sabit noktaları bulmak için, üç Rössler denklemi sıfıra ayarlanmıştır ve ( ${ displaystyle x}$ , ${ displaystyle y}$ , ${ displaystyle z}$ ) elde edilen denklemler çözülerek her sabit noktanın koordinatları belirlenmiştir. Bu, sabit nokta koordinatlarının her birinin genel denklemlerini verir ^[6]:

${ displaystyle { begin {case} x = { frac {c pm { sqrt {c ^ {2} -4ab}}} {2}} y = - left ({ frac {c pm { sqrt {c ^ {2} -4ab}}} {2a}} right) z = { frac {c pm { sqrt {c ^ {2} -4ab}}} {2a} } end {vakalar}}}$

Sırasıyla, belirli bir parametre değerleri kümesi için gerçek sabit noktaları göstermek için kullanılabilir:

{ displaystyle sol ({ frac {c + { sqrt {c ^ {2} -4ab}}} {2}}, { frac {-c - { sqrt {c ^ {2} -4ab}} } {2a}}, { frac {c + { sqrt {c ^ {2} -4ab}}} {2a}} sağ)}

{ displaystyle sol ({ frac {c - { sqrt {c ^ {2} -4ab}}} {2}}, { frac {-c + { sqrt {c ^ {2} -4ab}} } {2a}}, { frac {c - { sqrt {c ^ {2} -4ab}}} {2a}} sağ)}

Yukarıdaki Rössler Attraktörünün genel planlarında gösterildiği gibi, bu sabit noktalardan biri çeker döngüsünün merkezinde bulunur ve diğeri çekiciden nispeten uzakta bulunur.

Özdeğerler ve özvektörler

Bu sabit noktaların her birinin kararlılığı, ilgili özdeğerleri ve özvektörleri belirlenerek analiz edilebilir. Jacobian ile başlayarak:

${ displaystyle { begin {pmatrix} 0 & -1 & -1 1 & a & 0 z & 0 & x-c end {pmatrix}}}$

özdeğerler aşağıdaki kübik çözülerek belirlenebilir:

${ displaystyle - lambda ^ {3} + lambda ^ {2} (a + x-c) + lambda (ac-ax-1-z) + x-c + az = 0 ,}$

Merkezi olarak konumlandırılmış sabit nokta için, Rössler'in a = 0.2, b = 0.2 ve c = 5.7 olan orijinal parametre değerleri şu özdeğerleri verir:

{ displaystyle lambda _ {1} = 0,0971028 + 0.995786i ,}

{ displaystyle lambda _ {2} = 0.0971028-0.995786i ,}

{ displaystyle lambda _ {3} = - 5.68718 ,}

Negatif bir özdeğerin büyüklüğü, karşılık gelen özvektör boyunca çekim seviyesini karakterize eder. Benzer şekilde, pozitif bir özdeğerin büyüklüğü, karşılık gelen özvektör boyunca itme seviyesini karakterize eder.

Bu özdeğerlere karşılık gelen özvektörler şunlardır:

{ displaystyle v_ {1} = { begin {pmatrix} 0.7073 - 0.07278-0.7032i 0.0042-0.0007i end {pmatrix}}}

{ displaystyle v_ {2} = { begin {pmatrix} 0.7073 0.07278 + 0.7032i 0.0042 + 0.0007i end {pmatrix}}}

{ displaystyle v_ {3} = { begin {pmatrix} 0.1682 - 0.0286 0.9853 end {pmatrix}}}

Merkezi sabit nokta özvektörlerinin incelenmesi: Mavi çizgi, oluşturulan standart Rössler çekicisine karşılık gelir.

{ displaystyle a = 0.2}

,

{ displaystyle b = 0.2}

, ve

{ displaystyle c = 5.7}

.

İle Rössler çekicisi

{ displaystyle a = 0.2}

,

{ displaystyle b = 0.2}

,

{ displaystyle c = 5.7}

Bu özvektörlerin birkaç ilginç çıkarımı vardır. İlk olarak, iki özdeğer / özvektör çifti ( ${ displaystyle v_ {1}}$ ve ${ displaystyle v_ {2}}$ ) çekicinin ana diskinde meydana gelen sabit dışa doğru kaymadan sorumludur. Son özdeğer / özvektör çifti, manifoldun merkezinden geçen bir eksen boyunca çekiyor ve çeker içinde meydana gelen z hareketini açıklıyor. Bu etki kabaca aşağıdaki şekil ile gösterilmiştir.

Şekil, merkezi sabit nokta özvektörlerini inceler. Mavi çizgi, oluşturulan standart Rössler çekicisine karşılık gelir. ${ displaystyle a = 0.2}$ , ${ displaystyle b = 0.2}$ , ve ${ displaystyle c = 5.7}$ . Bu çekicinin ortasındaki kırmızı nokta ${ displaystyle FP_ {1}}$ . Bu sabit noktayı kesen kırmızı çizgi, tarafından üretilen itme düzleminin bir gösterimidir. ${ displaystyle v_ {1}}$ ve ${ displaystyle v_ {2}}$ . Yeşil çizgi, çekici olanın bir örneğidir. ${ displaystyle v_ {3}}$ . Eflatun çizgi, çeken özvektörün biraz yukarısında olan bir noktadan zamanda geriye doğru adım atılarak oluşturulur. ${ displaystyle FP_ {1}}$ - tamamen o vektör tarafından domine edilen noktaların davranışını gösterir. Eflatun çizginin, sabit noktaya yukarı doğru çekilmeden önce çekicinin düzlemine neredeyse temas ettiğine dikkat edin; bu, Rössler çekicinin genel görünümünün ve davranışının büyük ölçüde çekici arasındaki etkileşimin bir ürünü olduğunu gösterir. ${ displaystyle v_ {3}}$ ve itici ${ displaystyle v_ {1}}$ ve ${ displaystyle v_ {2}}$ uçak. Spesifik olarak, Rössler denklemlerinden üretilen bir dizinin dönmeye başlayacağı anlamına gelir. ${ displaystyle FP_ {1}}$ yukarı doğru çekilmeye başlayın ${ displaystyle v_ {3}}$ vektör, geri itme düzlemine doğru çekilirken tekrar dışarı doğru itilmeden önce vektöre doğru hafifçe içe doğru bükülen bir eğrinin yukarı doğru kolunu oluşturur.

Aykırı sabit nokta için Rössler'in orijinal parametre değerleri ${ displaystyle a = 0.2}$ , ${ displaystyle b = 0.2}$ , ve ${ displaystyle c = 5.7}$ özdeğerlerini verir:

{ displaystyle lambda _ {1} = - 0,0000046 + 5,4280259i}

{ displaystyle lambda _ {2} = - 0.0000046-5.4280259i}

{ displaystyle lambda _ {3} = 0,1929830}

Bu özdeğerlere karşılık gelen özvektörler şunlardır:

{ displaystyle v_ {1} = { begin {pmatrix} 0.0002422 + 0.1872055i 0.0344403-0.0013136i 0.9817159 end {pmatrix}}}

{ displaystyle v_ {2} = { begin {pmatrix} 0.0002422-0.1872055i 0.0344403 + 0.0013136i 0.9817159 end {pmatrix}}}

{ displaystyle v_ {3} = { begin {pmatrix} 0.0049651 - 0.7075770 0.7066188 end {pmatrix}}}

Bu özdeğerler ve özvektörler Rössler çekerinde bulunmasına rağmen, etkileri, başlangıç koşulları bu aykırı sabit noktaya genel yakın olan Rössler sisteminin yinelemeleri ile sınırlıdır. Başlangıç koşullarının oluşturduğu çekici düzlemde olduğu durumlar hariç ${ displaystyle lambda _ {1}}$ ve ${ displaystyle lambda _ {2}}$ Bu etki, sonuçta ortaya çıkan sistemi genel Rössler çekicisine doğru itmeyi içerir. Ortaya çıkan dizi merkezi sabit noktaya ve çekicinin kendisine yaklaştıkça, bu uzak sabit noktanın (ve özvektörlerinin) etkisi azalacaktır.

Poincaré haritası

Rössler çekicisinin Poincaré haritası ile

{ displaystyle a = 0.1}

,

{ displaystyle b = 0.1}

,

{ displaystyle c = 14}

Poincaré haritası belirli bir yönde ayarlanmış bir düzlemden her geçtiğinde işlevin değerini çizerek oluşturulur. Bir örnek, ${ displaystyle y, z}$ her geçtiğinde değer ${ displaystyle x = 0}$ uçak nerede ${ displaystyle x}$ Negatiften pozitife değişiyor, genellikle Lorenz çekicisini incelerken yapılır. Rössler çekicisi durumunda, ${ displaystyle x = 0}$ harita her zaman ${ displaystyle x = 0}$ uçak ${ displaystyle z = 0}$ Rössler denklemlerinin doğası gereği. İçinde ${ displaystyle x = 0.1}$ uçak için ${ displaystyle a = 0.1}$ , ${ displaystyle b = 0.1}$ , ${ displaystyle c = 14}$ , Poincaré haritası, ${ displaystyle z}$ değerler olarak ${ displaystyle x}$ Rössler grafiğinin yükselme ve bükülme bölümü nedeniyle bekleneceği gibi artar. Bu belirli Poincaré grafiğindeki nokta sayısı sonsuzdur, ancak farklı ${ displaystyle c}$ değer kullanılırsa, puan sayısı değişebilir. Örneğin, bir ${ displaystyle c}$ 4 değeri, Poincaré haritasında yalnızca bir nokta vardır, çünkü fonksiyon periyodik bir periyodik yörünge periyodu bir verir veya ${ displaystyle c}$ değer 12,8 olarak ayarlandığında, altı yörüngeye karşılık gelen altı nokta olacaktır.

Yerel maksimumları eşleme

{ displaystyle Z_ {n}}

vs.

{ displaystyle Z_ {n + 1}}

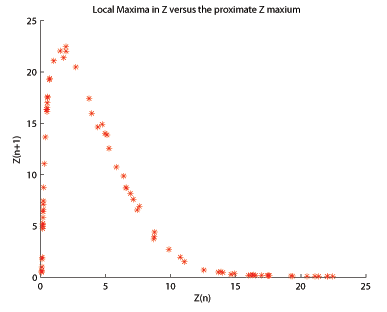
Lorenz Attractor hakkındaki orijinal makalede,^[7] Edward Lorenz yerel maksimumları analiz etti ${ displaystyle z}$ hemen önceki yerel maksimuma karşı. Görselleştirildiğinde, arsa, çadır haritası harita ve çeker arasında benzer analizlerin kullanılabileceğini ima eder. Rössler çekicisi için, ${ displaystyle z_ {n}}$ yerel maksimum, bir sonraki yerel bölgeye göre çizilir ${ displaystyle z}$ maksimum, ${ displaystyle z_ {n + 1}}$ ortaya çıkan arsa (burada gösterilen ${ displaystyle a = 0.2}$ , ${ displaystyle b = 0.2}$ , ${ displaystyle c = 5.7}$ ) tek modludur, çarpık bir Hénon haritası. Rössler çekicinin sahte bir 1-d harita oluşturmak için kullanılabileceğini bilerek, benzer analiz yöntemlerini kullanmaya devam eder. Çatallanma diyagramı özellikle yararlı bir analiz yöntemidir.

Parametrelerin değişimi

Rössler çekicinin davranışı büyük ölçüde sabit parametrelerinin değerlerinin bir faktörüdür ${ displaystyle a}$ , ${ displaystyle b}$ , ve ${ displaystyle c}$ . Genel olarak, her parametrenin değiştirilmesi, sistemin periyodik bir yörüngeye, sabit noktaya yakınsamasına veya sonsuza doğru kaçmasına neden olarak karşılaştırılabilir bir etkiye sahiptir, ancak indüklenen spesifik aralıklar ve davranışlar, her parametre için büyük ölçüde değişir. Rössler sisteminin periyodik yörüngeleri veya "birim döngüleri", döngü serileri kendini tekrar etmeye başlamadan önce ortaya çıkan merkezi nokta çevresindeki döngü sayısı ile tanımlanır.

Çatallanma diyagramları davranışlarını analiz etmek için yaygın bir araçtır. dinamik sistemler, bunlardan biri Rössler çekicisidir. Sistemin denklemlerini çalıştırarak, biri hariç tüm değişkenleri sabit tutarak ve sonuncuyu değiştirerek oluşturulurlar. Ardından, geçici faktörler etkisiz hale getirildikten sonra değişen değişken için belirli bir değerin ziyaret ettiği noktaların bir grafiği çizilir. Kaotik bölgeler, grafiğin doldurulmuş bölgeleri ile gösterilir.

Değişen bir

Buraya, ${ displaystyle b}$ 0.2'de sabitlenmiştir, ${ displaystyle c}$ 5,7 olarak sabitlenmiştir ve ${ displaystyle a}$ değişiklikler. Çekicinin değişim üzerindeki davranışının sayısal incelemesi ${ displaystyle a}$ çekicinin davranışı üzerinde orantısız bir etkiye sahip olduğunu öne sürer. Analizin sonuçları:

${ displaystyle a leq 0}$ : Merkezi konumdaki sabit noktaya yakınsar
${ displaystyle a = 0.1}$ : 1. periyodun birim döngüsü
${ displaystyle a = 0.2}$ : Rössler tarafından seçilen standart parametre değeri, kaotik
${ displaystyle a = 0.3}$ : Kaotik çeker, önemli ölçüde daha fazla Mobius şeridi -like (kendi üzerine katlanır).
${ displaystyle a = 0,35}$ : 0,3'e benzer, ancak giderek kaotik
${ displaystyle a = 0,38}$ : .35'e benzer, ancak giderek kaotik.

Değişen b

Değişkenler için Rössler çekicinin çatallanma diyagramı

{ displaystyle b}

Buraya, ${ displaystyle a}$ 0.2'de sabitlenmiştir, ${ displaystyle c}$ 5,7 olarak sabitlenmiştir ve ${ displaystyle b}$ değişiklikler. Ekteki diyagramda gösterildiği gibi, ${ displaystyle b}$ 0'a yaklaşır çeker sonsuza yaklaşır (çok küçük değerler için yükselişe dikkat edin ${ displaystyle b}$ . Diğer parametrelerle karşılaştırmalı, değişken ${ displaystyle b}$ periyot-3 ve periyot-6 yörüngeleri oluştuğunda daha büyük bir menzil üretir. Kıyasla ${ displaystyle a}$ ve ${ displaystyle c}$ , daha yüksek değerler ${ displaystyle b}$ kaotik bir duruma değil, dönem-1'e yakınsar.

Değişen c

Değişkenler için Rössler çekicinin çatallanma diyagramı

{ displaystyle c}

Buraya, ${ displaystyle a = b = 0.1}$ ve ${ displaystyle c}$ değişiklikler. çatallanma diyagramı düşük değerlerin ${ displaystyle c}$ periyodiktir, ancak hızla kaotik hale gelir ${ displaystyle c}$ artışlar. Bu model kendini şu şekilde tekrar eder: ${ displaystyle c}$ artışlar - kaos dönemleriyle serpiştirilmiş periyodiklik bölümleri vardır ve eğilim, daha yüksek dönem yörüngelerine doğru ${ displaystyle c}$ artışlar. Örneğin, bir yörünge periyodu yalnızca aşağıdaki değerler için görünür: ${ displaystyle c}$ 4 civarıdır ve çatallanma diyagramında bir daha asla bulunmaz. Aynı fenomen üçüncü periyotta da görülür; a kadar ${ displaystyle c = 12}$ , periyot üç yörünge bulunabilir, ancak daha sonra görünmezler.

Bir aralıktaki değişen çekicinin grafiksel bir gösterimi ${ displaystyle c}$ değerler, tüm bu parametre analizleri için görülen genel davranışı gösterir - periyodiklik ve periyodiklik arasındaki sık geçişler.

Değişen c

c = 4, dönem 1

c = 6, dönem 2

c = 8.5, dönem 4

c = 8.7, dönem 8

c = 9, kaotik

c = 12, dönem 3

c = 12.6, dönem 6

c = 13, kaotik

c = 18, kaotik

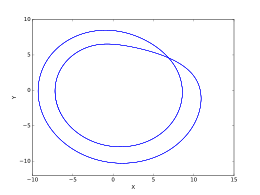
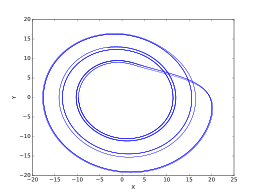
Yukarıdaki resim seti, geçici sonrası Rössler sistemindeki varyasyonları şu şekilde göstermektedir: ${ displaystyle c}$ bir değer aralığında çeşitlidir. Bu görüntüler ile oluşturuldu ${ displaystyle a = b = .1}$ .

${ displaystyle c = 4}$ , nokta-1 yörünge.
${ displaystyle c = 6}$ , nokta-2 yörüngesi.
${ displaystyle c = 8.5}$ , periyot-4 yörünge.
${ displaystyle c = 8.7}$ , nokta-8 yörünge.
${ displaystyle c = 9}$ , seyrek kaotik çeker.
${ displaystyle c = 12}$ , nokta-3 yörünge.
${ displaystyle c = 12,6}$ , nokta-6 yörünge.
${ displaystyle c = 13}$ , seyrek kaotik çeker.
${ displaystyle c = 18}$ , dolu kaotik çeker.

Periyodik Yörüngeler

Çeker yoğun bir şekilde doldurulur periyodik yörüngeler: sıfır olmayan bir değeri olan çözümler ${ displaystyle T}$ öyle ki ${ displaystyle { vec {x}} (t + T) = { vec {x}} (t)}$ . Bu ilginç çözümler sayısal olarak türetilebilir. Newton yöntemi. Periyodik yörüngeler, fonksiyonun kökleridir ${ displaystyle Phi _ {t} -Id}$ , nerede ${ displaystyle Phi _ {t}}$ zamana göre evrim ${ displaystyle t}$ ve ${ displaystyle Kimliği}$ kimliktir. Dinamiklerin çoğunluğu x-y düzleminde meydana geldiğinden, periyodik yörüngeler daha sonra kendilerine göre sınıflandırılabilir. sargı numarası projeksiyondan sonra merkezi denge etrafında.

Sargı Numarasına Göre Periyodik Yörüngeler Tablosu k

k=1

k = 2

k = 3

Zaman ölçeklenemez. Orijinal parametreler (a, b, c) = (0.2,0.2,5.7) kullanıldı.

Sayısal deneylerden, tüm pozitif sargı sayıları için benzersiz bir periyodik yörünge olduğu görülmektedir. Bu yozlaşma eksikliği, muhtemelen sorunun simetri eksikliğinden kaynaklanıyor. Çeker, sindirimi daha kolay olacak şekilde parçalara ayrılabilir değişmez manifoldlar: 1D periyodik yörüngeler ve 2D kararlı ve kararsız manifoldlar periyodik yörüngeler. Bu değişmez manifoldlar, çekicinin doğal bir iskeletidir, tıpkı rasyonel sayılar ... için gerçek sayılar.

Amaçları için dinamik sistemler teorisi Biri ilgilenebilir topolojik değişmezler bu manifoldların. Periyodik yörüngeler, ${ displaystyle S ^ {1}}$ gömülü ${ displaystyle mathbb {R} ^ {3}}$ , böylece topolojik özellikleri ile anlaşılabilir düğüm teorisi. Sargı numaraları 1 ve 2 olan periyodik yörüngeler, bir Hopf bağlantısı, hayır göstererek diffeomorfizm bu yörüngeleri ayırabilir.

Diğer konulara bağlantılar

Rössler çekicisindeki bantlaşma, bir Kantor seti orta noktası etrafında döndürüldü. Ek olarak, Rössler çekerinde meydana gelen yarım bükülme, çekicinin yalnızca bir bölümünü etkiler. Rössler, çekicisinin aslında "normal bir grup" ile bir Mobius şeridi.^[8]

Referanslar

^ ^a ^b ^c Rössler, O. E. (1976), "Sürekli Kaos İçin Bir Denklem", Fizik Mektupları, 57A (5): 397–398, Bibcode:1976PhLA ... 57..397R, doi:10.1016/0375-9601(76)90101-8.
^ Rössler, O. E. (1979), "Hyperchaos için Bir Denklem", Fizik Mektupları, 71A (2, 3): 155–157, Bibcode:1979PhLA ... 71..155R, doi:10.1016/0375-9601(79)90150-6.
^ ^a ^b Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar (2004), "12.3 Rössler Çekicisi", Kaos ve Fraktallar: Bilimin Yeni Sınırları, Springer, s. 636–646.
^ Letellier, C .; P. Dutertre; B. Maheu (1995). "Rössler sisteminin kararsız periyodik yörüngeleri ve şablonları: sistematik bir topolojik karakterizasyona doğru". Kaos. 5 (1): 272–281. Bibcode:1995Chaos ... 5..271L. doi:10.1063/1.166076.
^ Letellier, C .; V. Messager (2010). "Otto E. Rössler'in kaos hakkındaki ilk makalesi üzerindeki etkiler". International Journal of Bifurcation & Chaos. 20 (11): 3585–3616. Bibcode:2010IJBC ... 20.3585L. doi:10.1142 / s0218127410027854.
^ Martines-Arano, H .; Garcia-Pérez, B.E .; Vidales-Hurtado, M.A .; Trejo-Valdez, M .; Hernández-Gómez, L.H .; Torres-Torres, C. (2019). "Hücreli Au Nanopartiküllerde Plazmonik Etkiler Tarafından Sergilenen Kaotik İmzalar". Sensörler. 19: 4728.CS1 Maint: birden çok isim: yazarlar listesi (bağlantı)
^ Lorenz, E.N. (1963), "Deterministik periyodik olmayan akış", J. Atmos. Sci., 20 (2): 130–141, Bibcode:1963JAtS ... 20..130L, doi:10.1175 / 1520-0469 (1963) 020 <0130: DNF> 2.0.CO; 2.
^ Rössler, Otto E. (1976). "Basit reaksiyon sisteminde kaotik davranış". Zeitschrift für Naturforschung A. 31 (3–4): 259–264. Bibcode:1976ZNatA..31..259R. doi:10.1515 / zna-1976-3-408.

Dış bağlantılar

Flash Animasyon kullanma PovRay
Rossler1976.pdf
Lorenz ve Rössler çekiciler - Java animasyonu
3D Çekiciler: Rössler ve Lorenz çekicilerini 3 boyutlu olarak görselleştirmek ve keşfetmek için Mac programı
Scholarpedia'daki Rössler çekicisi
Rössler Attractor: 3 boyutlu sayısal etkileşimli deney - deneyimler.math.cnrs.fr- (javascript / webgl)

[r76-1] Rössler, O. E. (1976), "Sürekli Kaos İçin Bir Denklem", Fizik Mektupları, 57A (5): 397–398, Bibcode:1976PhLA ... 57..397R, doi:10.1016/0375-9601(76)90101-8.

[r79-2] Rössler, O. E. (1979), "Hyperchaos için Bir Denklem", Fizik Mektupları, 71A (2, 3): 155–157, Bibcode:1979PhLA ... 71..155R, doi:10.1016/0375-9601(79)90150-6.

[cfnf-3] Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar (2004), "12.3 Rössler Çekicisi", Kaos ve Fraktallar: Bilimin Yeni Sınırları, Springer, s. 636–646.

[4] Letellier, C .; P. Dutertre; B. Maheu (1995). "Rössler sisteminin kararsız periyodik yörüngeleri ve şablonları: sistematik bir topolojik karakterizasyona doğru". Kaos. 5 (1): 272–281. Bibcode:1995Chaos ... 5..271L. doi:10.1063/1.166076.

[5] Letellier, C .; V. Messager (2010). "Otto E. Rössler'in kaos hakkındaki ilk makalesi üzerindeki etkiler". International Journal of Bifurcation & Chaos. 20 (11): 3585–3616. Bibcode:2010IJBC ... 20.3585L. doi:10.1142 / s0218127410027854.

[6] Martines-Arano, H .; Garcia-Pérez, B.E .; Vidales-Hurtado, M.A .; Trejo-Valdez, M .; Hernández-Gómez, L.H .; Torres-Torres, C. (2019). "Hücreli Au Nanopartiküllerde Plazmonik Etkiler Tarafından Sergilenen Kaotik İmzalar". Sensörler. 19: 4728.CS1 Maint: birden çok isim: yazarlar listesi (bağlantı)

[7] Lorenz, E.N. (1963), "Deterministik periyodik olmayan akış", J. Atmos. Sci., 20 (2): 130–141, Bibcode:1963JAtS ... 20..130L, doi:10.1175 / 1520-0469 (1963) 020 <0130: DNF> 2.0.CO; 2.

[8] Rössler, Otto E. (1976). "Basit reaksiyon sisteminde kaotik davranış". Zeitschrift für Naturforschung A. 31 (3–4): 259–264. Bibcode:1976ZNatA..31..259R. doi:10.1515 / zna-1976-3-408.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]