Sallanan Atwoods makinesi - Swinging Atwoods machine - Wikipedia
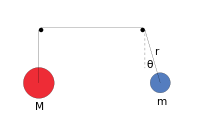
Atwood'un makinesini sallamak (SAM), basit bir Atwood'un makinesi kütlelerden birinin iki boyutlu bir düzlemde sallanmasına izin verilmesi dışında dinamik sistem yani kaotik bazı sistem parametreleri için ve başlangıç koşulları.
Spesifik olarak iki kütleden oluşur (sarkaç, kütle ve karşı ağırlık, kütle ) bir uzayamaz, kütlesiz ip ikiye asılı sürtünmesiz kasnaklar sarkaç, karşı ağırlık ile çarpışmadan kasnağı etrafında serbestçe dönebilecek şekilde sıfır yarıçaplıdır.[1]
Geleneksel Atwood'un makinesi yalnızca "kaçak" çözümlere izin verir (yani sarkaç veya karşı ağırlık sonunda kasnağıyla çarpışır), hariç . Ancak, sallanan Atwood'un makinesi büyük parametre alanı Sonlandıran veya sonlandırmayan, periyodik, yarı periyodik veya kaotik, sınırlı veya sınırsız, tekil veya tekil olmayan olarak sınıflandırılabilen çeşitli hareketlere yol açan koşulların[1][2] sarkaç nedeniyle reaktif merkezkaç kuvveti karşı ağırlığın ağırlığını dengelemek.[1] SAM ile ilgili araştırma, 1982 tarihli bir üst düzey tezin parçası olarak başladı. Gülümsemeler ve Gözyaşları (sistemin bazı yörüngelerinin şekline atıfta bulunarak) Nicholas Tufillaro -de Reed Koleji, yöneten David J. Griffiths.[3]
Hareket denklemleri

Sallanan Atwood'un makinesi iki serbestlik derecesine sahip bir sistemdir. Hareket denklemlerini ikisinden birini kullanarak türetebiliriz Hamilton mekaniği veya Lagrange mekaniği. Sallanan kütle olsun ve sallanmayan kütle . Sistemin kinetik enerjisi, , dır-dir:
nerede sallanan kütlenin eksenine olan mesafesidir ve sallanan kütlenin aşağıya doğru bakmaya göre açısıdır. Potansiyel enerji sadece yer çekiminden kaynaklanan ivme:
Daha sonra Lagrangian'ı yazabiliriz, ve Hamiltoniyen, sistemin:
Daha sonra Hamiltoniyeni kanonik momenta cinsinden ifade edebiliriz, , :
Lagrange analizi, iki adet ikinci dereceden birleştirilmiş adi diferansiyel denklem elde etmek için uygulanabilir. ve . İlk önce denklem:
Ve denklem:
Kütle oranını tanımlayarak denklemleri basitleştiriyoruz . Yukarıdakiler şu hale gelir:
Hamilton analizi, aynı zamanda, dört birinci dereceden ODE'yi belirlemek için de uygulanabilir. , ve bunlara karşılık gelen kanonik momenta ve :
Bu türetmelerin her ikisinde de, eğer biri ayarlanmışsa ve açısal hız sıfıra gelindiğinde ortaya çıkan özel durum, normal sallanmayan durumdur. Atwood makinesi:
Sallanan Atwood'un makinesinin dört boyutlu bir faz boşluğu tarafından tanımlandı , ve bunlara karşılık gelen kanonik momenta ve . Bununla birlikte, enerji tasarrufu nedeniyle, faz uzayı üç boyutla sınırlandırılmıştır.
Büyük kasnaklı sistem
Sistemdeki kasnaklar varsa eylemsizlik momenti ve yarıçap SAM Hamiltoniyeni o zaman:[4]
Nerede Mt sistemin efektif toplam kütlesi,
Bu, aşağıdaki durumlarda yukarıdaki sürüme indirgenir ve sıfır olur. Hareket denklemleri şimdi:[4]
nerede .
Entegre edilebilirlik
Hamilton sistemleri olarak sınıflandırılabilir entegre edilebilir ve entegre edilemez. SAM, kütle oranı olduğunda entegre edilebilir .[5] Sistem ayrıca şunlar için oldukça düzenli görünüyor: , ama durum bilinen tek integrallenebilir kütle oranıdır. Sistemin entegre edilemeyeceği gösterilmiştir. .[6] Kütle oranının (ve başlangıç koşullarının) diğer birçok değeri için SAM görüntülenir kaotik hareket.
Sayısal çalışmalar, yörünge tekil olduğunda (başlangıç koşulları: ), sarkaç tek bir simetrik döngü yürütür ve değerine bakılmaksızın başlangıç noktasına geri döner. . Ne zaman küçüktür (dikeye yakın), yörünge bir "gözyaşı damlasını" tanımlar, büyük olduğunda bir "kalbi" tanımlar. Bu yörüngeler, doğrusal olmayan Hamiltoniyenli bir sistem için alışılmadık bir durum olan cebirsel olarak tam olarak çözülebilir.[7]
Yörüngeler
Sallanan Atwood'un makinesinin sallanan kütlesi, farklı başlangıç koşullarına tabi olduğunda ve farklı kütle oranları için ilginç yörüngelerden veya yörüngelerden geçer. Bunlar, periyodik yörüngeleri ve çarpışma yörüngelerini içerir.
Tekil olmayan yörüngeler
Belirli koşullar için sistem şunları gösterir karmaşık harmonik hareket.[1] Sallanan kütle kasnağa temas etmiyorsa yörüngeye tekil olmayan denir.
- Tekil olmayan yörüngelerin seçimi

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.
Periyodik yörüngeler

Sistemdeki farklı harmonik bileşenler fazda olduğunda, ortaya çıkan yörünge basit ve periyodiktir, örneğin sıradan bir "gülümseme" yörüngesi gibi. sarkaç ve çeşitli döngüler.[3][8] Genel olarak, aşağıdakiler karşılandığında periyodik bir yörünge vardır:[1]
Periyodik yörüngelerin en basit örneği, Tufillaro'nun dediği "gülümseme" yörüngesidir. A yazın 1984 tarihli makalesinde yörüngeler.[1]
- Periyodik yörüngelerin seçimi

Sallanan Atwood'un makinesinin bir "gülümseme" yörüngesi, , ve sıfır başlangıç hızı.
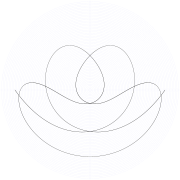
Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.
Tekil yörüngeler
Hareket, bir noktada sallanan kütle başlangıç noktasından geçerse tekildir. Sistem olduğundan değişmez zamanın tersine çevrilmesi ve çevrilmesi altında, sarkacın başlangıçta başladığını ve dışarı doğru ateşlendiğini söylemekle eşdeğerdir:[1]
Eksene yakın bölge tekildir, çünkü sıfıra yakın ve hareket denklemlerinin bölünmesi gerekiyor . Bu nedenle, bu durumları titizlikle analiz etmek için özel teknikler kullanılmalıdır.[9]
Aşağıdakiler, keyfi olarak seçilen tekil yörüngelerin çizimidir.
- Tekil yörüngelerin seçimi

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.

Sallanan Atwood'un makinesinin bir yörüngesi , ve sıfır başlangıç hızı.
Çarpışma yörüngeleri
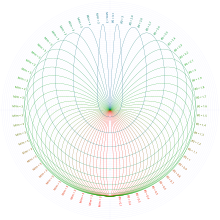
Çarpışma (veya sona eren tekil) yörüngeler, sallanan kütle kendi ekseninden bir başlangıç hızıyla çıkarıldığında oluşan tekil yörüngelerin alt kümesidir, öyle ki, eksene geri döner (yani, pivot ile çarpışır):
En basit çarpışma yörüngeleri, kütle oranı 3 olan ve başlangıç noktasından çıkarıldıktan sonra daima simetrik olarak başlangıç noktasına geri dönecek olan yörüngelerdir ve adı verilmiştir. B Tipi Tufillaro'nun ilk makalesinde yörüngeler.[1] Görünüşlerinden dolayı gözyaşı damlası, kalp veya tavşan kulağı yörüngeleri olarak da adlandırılırlar.[3][7][8][9]
Sallanan kütle başlangıç noktasına geri döndüğünde, karşı ağırlık kütlesi, anında yön değiştirmeli ve bağlantı dizisinde sonsuz bir gerilime neden olmalıdır. Bu nedenle, hareketin şu anda sona ermesini düşünebiliriz.[1]
Sınırlılık
Herhangi bir başlangıç konumu için, sallanan kütlenin bir eğri ile sınırlandığı gösterilebilir. konik kesit.[2] Pivot her zaman bir odak bu sınırlayıcı eğrinin. Bu eğri için denklem, sistemin enerjisi analiz edilerek ve enerjinin korunumu kullanılarak elde edilebilir. Farz edelim ki dinlenmeden serbest bırakıldı ve . Sistemin toplam enerjisi bu nedenle:
Bununla birlikte, sınır durumunda, sallanan kütlenin hızının sıfır olduğuna dikkat edin.[2] Dolayısıyla bizde:
Bunun bir konik bölümün denklemi olduğunu görmek için, :
Başlangıç koşulunun hareketsiz olduğunu varsaydığımız için, bu durumda payın yalnızca başlangıç konumuna bağlı bir sabit olduğuna dikkat edin. Ancak enerji sabiti sıfır olmayan başlangıç hızı için de hesaplanabilir ve denklem her durumda hala geçerlidir.[2] eksantriklik konik bölümün . İçin , bu bir elipstir ve sistem sınırlıdır ve sallanan kütle her zaman elips içinde kalır. İçin bu bir paraboldür ve o bir hiperbol; bu iki durumda da sınırlı değildir. Gibi keyfi olarak büyür, sınırlayıcı eğri bir daireye yaklaşır. Eğrinin çevrelediği bölge Hill bölgesi olarak bilinir.[2]
Son üç boyutlu uzatma
Üç boyutlu Swinging Atwood Makinesi (3D-SAM) problemi için yeni bir entegre edilebilir durum 2016'da açıklandı.[10] 2D sürüm gibi, sorun ne zaman entegre edilebilir? .
Referanslar
- ^ a b c d e f g h ben Tufillaro, Nicholas B .; Abbott, Tyler A .; Griffiths, David J. (1984). "Sallanan Atwood'un Makinesi". Amerikan Fizik Dergisi. 52 (10): 895–903. Bibcode:1984 AmJPh..52..895T. doi:10.1119/1.13791.
- ^ a b c d e Tufillaro, Nicholas B .; Nunes, A .; Casasayas, J. (1988). "Sallanan Atwood'un makinesinin sınırsız yörüngeleri". Amerikan Fizik Dergisi. 56: 1117. Bibcode:1988AmJPh..56.1117T. doi:10.1119/1.15774.
- ^ a b c Tufillaro, Nicholas B. (1982). Gülümsemeler ve Gözyaşları (Tez). Reed Koleji.
- ^ a b Pujol, Olivier; Perez, J.P .; Simo, C .; Simon, S .; Weil, J.A. (2010). "Sallanan Atwood'un Makinesi: Deneysel ve sayısal sonuçlar ve teorik bir çalışma". Physica D. 239 (12): 1067–1081. arXiv:0912.5168. Bibcode:2010PhyD..239.1067P. doi:10.1016 / j.physd.2010.02.017.
- ^ Tufillaro, Nicholas B. (1986). "Sallanan bir Atwood makinesinin entegre edilebilir hareketi". Amerikan Fizik Dergisi. 54 (2): 142. Bibcode:1986AmJPh..54..142T. doi:10.1119/1.14710.
- ^ Casasayas, J .; Nunes, A .; Tufillaro, N. (1990). "Sallanan Atwood'un Makinesi: bütünleştirilebilirlik ve dinamikler". Journal de Physique. 51 (16): 1693–1702. doi:10.1051 / jphys: 0199000510160169300. ISSN 0302-0738.
- ^ a b Tufillaro, Nicholas B. (1994). "Sallanan bir Atwoods makinesinin gözyaşı ve kalp yörüngeleri". Amerikan Fizik Dergisi. 62 (3): 231–233. arXiv:chao-dyn / 9302006. Bibcode:1994 AmJPh..62..231T. doi:10.1119/1.17602.
- ^ a b Tufillaro, Nicholas B. (1985). "Sallanan Atwood'un makinesinin hareketleri". Journal de Physique. 46 (9): 1495–1500. doi:10.1051 / jphys: 019850046090149500.
- ^ a b Tufillaro, Nicholas B. (1985). "Sallanan Atwood'un makinesinin çarpışma yörüngeleri" (PDF). Journal de Physique. 46: 2053–2056. doi:10.1051 / jphys: 0198500460120205300.
- ^ Elmandouh, A.A. (2016). "3B Sallanan Atwood makinesinin hareketinin bütünleştirilebilirliği ve ilgili sorunlar hakkında". Fizik Harfleri A. 380: 989. Bibcode:2016PhLA..380..989E. doi:10.1016 / j.physleta.2016.01.021.
daha fazla okuma
- Almeida, M.A., Moreira, I.C. ve Santos, F.C. (1998) "Bazı homojen hamilton sistem sınıfları için Ziglin-Yoshida analizi üzerine", Brezilya Fizik Dergisi Cilt 28 n. 4 São Paulo Aralık.
- Barrera, Emmanuel Jan (2003) Çift Sallanan Atwood'un makinesinin dinamiği, B.S. Tez, Ulusal Fizik Enstitüsü, Filipinler Üniversitesi.
- Babelon, O, M. Talon, MC Peyranere (2010), "Kowalevski'nin sallanan Atwood'un makinesine ilişkin analizi," Journal of Physics A: Matematiksel ve Teorik Cilt 43 (8).
- Bruhn, B. (1987) "Doğrusal olmayan osilatörlerin zayıf eşleşmiş sistemlerinde kaos ve düzen," Physica Scripta Cilt 35 (1).
- Casasayas, J., N. B. Tufillaro ve A. Nunes (1989) "Sallanan Atwood'un makinesinin sonsuzluk manifoldu", Avrupa Fizik Dergisi Cilt 10 (10), s173.
- Casasayas, J, A. Nunes ve N. B. Tufillaro (1990) "Swinging Atwood's machine: integrability and dynamics" Journal de Physique Cilt 51, s1693.
- Chowdhury, A. Roy ve M. Debnath (1988) "Sallanan Atwood Makinesi. Uzak ve yakın rezonans bölgesi", International Journal of Theoretical Physics, Cilt. 27 (11), sayfa 1405-1410.
- Griffiths D. J. ve T. A. Abbott (1992) "" Şaşırtıcı bir mekanik gösterimi "üzerine yorum, Amerikan Fizik Dergisi Cilt 60 (10), s951-953.
- Moreira, I.C. ve M.A. Almeida (1991) "Noether simetrileri ve Swinging Atwood Makinesi", Journal of Physics II Fransa 1, s711-715.
- Nunes, A., J. Casasayas ve N. B. Tufillaro (1995) "Bütünleşik sallanan Atwood'un makinesinin periyodik yörüngeleri" Amerikan Fizik Dergisi Cilt 63 (2), sayfa 121-126.
- Ouazzani-T.H., A. ve Ouzzani-Jamil, M., (1995) "Sallanan Atwood'un makinesinin bütünleştirilebilir bir durumunun Liouville tori'nin çatallanması" Il Nuovo Cimento B Cilt 110 (9).
- Olivier, Pujol, JP Perez, JP Ramis, C. Simo, S. Simon, JA Weil (2010), "Swinging Atwood's Machine: Experimental and numical results, and a teorik çalışma," Physica D 239, s. 1067–1081.
- Sears, R. (1995) "Şaşırtıcı bir mekanik gösterimi" üzerine yorum, Amerikan Fizik Dergisi, Cilt. 63 (9), s854-855.
- Yehia, H.M., (2006) "Eğik bir koni üzerindeki ağır bir parçacığın hareketinin ve sallanan Atwood makinesinin bütünleştirilebilirliği üzerine", Mekanik Araştırma İletişimi Cilt 33 (5), p711–716.
Dış bağlantılar
- Lisans araştırmalarında kullanım örneği: semplektik entegratörler
- Imperial College Kursu
- Oscilaciones en la máquina de Atwood
- "Gülümsemeler ve Gözyaşları" (1982)
- 2007 Çalıştayı
- Deneysel Sallanan Atwood'un Makinesinin 2010 Videoları
- 2010 APS Toplantısında Sallanan Atwood'un Makinesi ile İlgili Güncelleme, 19 Mart 2010 Cuma, 08:24, Portland, OR
- Swinging Atwood's Machine'in interaktif web uygulaması
- Swinging Atwood's Machine'i çalıştırmak için açık kaynaklı Java kodu
















































































