Pratik numara - Practical number

12 sayısının pratikliğinin gösterilmesi

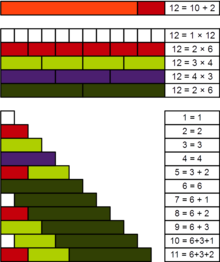
İçinde sayı teorisi, bir pratik sayı veya panaritmik sayı^[1] pozitif bir tam sayıdır n öyle ki tüm daha küçük pozitif tamsayılar farklı toplamlar olarak temsil edilebilir bölenler nın-nin n. Örneğin, 12 pratik bir sayıdır, çünkü 1'den 11'e kadar olan tüm sayılar, bölenleri 1, 2, 3, 4 ve 6'nın toplamı olarak ifade edilebilir: ve bu bölenlerin kendilerinin yanı sıra 5 = 3 + 2'ye sahibiz, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1 ve 11 = 6 + 3 + 2.

Pratik sayıların dizisi (sıra A005153 içinde OEIS ) başlar

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

Pratik numaralar tarafından kullanıldı Fibonacci onun içinde Liber Abaci (1202) rasyonel sayıları şu şekilde temsil etme sorunu ile bağlantılı olarak Mısır kesirleri. Fibonacci resmi olarak pratik sayıları tanımlamaz, ancak pratik paydalara sahip kesirler için Mısır kesir açılımlarının bir tablosunu verir.^[2]

"Pratik sayı" adı, Srinivasan (1948). "Paranın, ağırlıkların ve ölçülerin alt bölümleri 4, 12, 16, 20 ve 28 gibi sayılardan oluştuğunu ve bunların genellikle 10'luk kuvvetlerle değiştirilmeyi hak edecek kadar sakıncalı olduğunu" belirtti. Bu tür sayıların sayı teorik özelliğini yeniden keşfetti ve bu sayıların sınıflandırmasını yapan ilk kişi oldu. Stewart (1954) ve Sierpiński (1955). Bu karakterizasyon, asal çarpanlara ayırmayı inceleyerek bir sayının pratik olup olmadığını belirlemeyi mümkün kılar. Her çift mükemmel numara ve hepsi ikinin gücü aynı zamanda pratik bir sayıdır.

Pratik sayıların da benzer olduğu gösterilmiştir. asal sayılar özelliklerinin çoğunda.^[3]

Pratik sayıların karakterizasyonu

Orijinal karakterizasyon Srinivasan (1948) pratik bir sayının bir eksik numara yani, eksiklik bir olmadıkça, tüm bölenlerin toplamı (1 ve kendisi dahil) sayının iki katından daha azdır. Pratik sayının tüm bölenlerinin sıralı kümesi ${ displaystyle n}$ dır-dir ${ displaystyle {d_ {1}, d_ {2}, ..., d_ {j}}}$ ile ${ displaystyle d_ {1} = 1}$ ve ${ displaystyle d_ {j} = n}$, o zaman Srinivasan'ın ifadesi eşitsizlikle ifade edilebilir

${ displaystyle 2n leq 1+ toplam _ {i = 1} ^ {j} d_ {i}}$.

Başka bir deyişle, tüm bölenlerin sıralı dizisi ${ displaystyle {d_ {1}$ pratik bir sayının tam alt sıra.

Bu kısmi karakterizasyon genişletildi ve tamamlandı Stewart (1954) ve Sierpiński (1955) bir sayının pratik olup olmadığını belirlemenin kolay olduğunu gösteren asal çarpanlara ayırma Asal çarpanlara ayırma ile birden büyük pozitif bir tam sayı ${ displaystyle n = p_ {1} ^ { alpha _ {1}} ... p_ {k} ^ { alpha _ {k}}}$ (sıralı sırayla asallarla ${ displaystyle p_ {1}$) pratiktir ancak ve ancak asal faktörlerinin her biri ${ displaystyle p_ {i}}$ için yeterince küçük ${ displaystyle p_ {i} -1}$ daha küçük bölenlerin toplamı olarak temsil edilmesi. Bunun doğru olması için ilk asal ${ displaystyle p_ {1}}$ 2'ye eşit olmalı ve her biri için ben 2'denk, her ardışık asal ${ displaystyle p_ {i}}$ eşitsizliğe uymalı

${ displaystyle p_ {i} leq 1+ sigma (p_ {1} ^ { alpha _ {1}} p_ {2} ^ { alpha _ {2}} noktalar p_ {i-1} ^ { alpha _ {i-1}}) = 1+ prod _ {j = 1} ^ {i-1} { frac {p_ {j} ^ { alpha _ {j} +1} -1} { p_ {j} -1}},}$

nerede ${ displaystyle sigma (x)}$ gösterir bölenlerin toplamı nın-nin x. Örneğin, 2 × 3² × 29 × 823 = 429606 pratiktir, çünkü yukarıdaki eşitsizlik asal faktörlerinin her biri için geçerlidir: 3 ≤ σ (2) + 1 = 4, 29 ≤ σ (2 × 3²) + 1 = 40 ve 823 ≤ σ (2 × 3² × 29) + 1 = 1171.

Bir sayının uygulanabilir olması için yukarıda belirtilen koşul gerekli ve yeterlidir. Bir yönde, temsil edebilmek için bu koşul gereklidir. ${ displaystyle p_ {i} -1}$ bölenlerin toplamı olarak nçünkü eşitsizlik doğru olamazsa, tüm küçük bölenleri bir araya getirmek bile ulaşılamayacak kadar küçük bir toplam verirdi ${ displaystyle p_ {i} -1}$. Diğer yönde, tümevarımla da görülebileceği gibi koşul yeterlidir. Daha güçlü bir şekilde, çarpanlara ayırma n yukarıdaki koşulu karşılarsa ${ Displaystyle m leq sigma (n)}$ bölenlerin toplamı olarak temsil edilebilir n, aşağıdaki adımlar sırasına göre:^[4]

• İndüksiyon ile ${ displaystyle j in [1, alpha _ {k}]}$gösterilebilir ki ${ displaystyle p_ {k} ^ {j} leq 1+ sigma (n / p_ {k} ^ { alpha _ {k} - (j-1)})}$. Bu nedenle ${ displaystyle p_ {k} ^ { alpha _ {k}} leq 1+ sigma (n / p_ {k})}$.
• İçeriden beri ${ displaystyle [qp_ {k} ^ { alpha _ {k}}, qp_ {k} ^ { alpha _ {k}} + sigma (n / p_ {k})]}$ örtmek ${ displaystyle [1, sigma (n)]}$ için ${ displaystyle 1 leq q leq sigma (n / p_ {k} ^ { alpha _ {k}})}$böyle bir ${ displaystyle q}$ ve bazı ${ displaystyle r in [0, sigma (n / p_ {k})]}$ öyle ki ${ displaystyle m = qp_ {k} ^ { alpha _ {k}} + r}$.
• Dan beri ${ displaystyle q leq sigma (n / p_ {k} ^ { alpha _ {k}})}$ ve ${ displaystyle n / p_ {k} ^ { alpha _ {k}}}$ tümevarımla pratik olarak gösterilebilir, bir temsilini bulabiliriz q bölenlerin toplamı olarak ${ displaystyle n / p_ {k} ^ { alpha _ {k}}}$.
• Dan beri ${ displaystyle r leq sigma (n / p_ {k})}$, dan beri ${ displaystyle n / p_ {k}}$ tümevarımla pratik olarak gösterilebilir, bir temsilini bulabiliriz r bölenlerin toplamı olarak ${ displaystyle n / p_ {k}}$.
• Temsil eden bölenler r, birlikte ${ displaystyle p_ {k} ^ { alpha _ {k}}}$ çarpı bölenlerin her birinin temsil ettiği qbirlikte bir temsilini oluşturur m bölenlerin toplamı olarak n.

Özellikleri

• Tek tek pratik sayı 1'dir, çünkü eğer n > 2 tek bir sayıdır, bu durumda 2'nin farklı bölenlerinin toplamı olarak ifade edilemezn. Daha güçlü, Srinivasan (1948) 1 ve 2 dışındaki her pratik sayının 4 veya 6'ya (veya her ikisine) bölünebileceğini gözlemler.
• İki pratik sayının çarpımı da pratik bir sayıdır.^[5] Daha güçlü en küçük ortak Kat herhangi iki pratik sayıdan biri de pratik bir sayıdır. Aynı şekilde, tüm pratik sayılar kümesi çarpma altında kapatılır.
• Stewart ve Sierpiński tarafından yapılan yukarıdaki tanımlamadan, eğer n pratik bir sayıdır ve d bölenlerinden biri o zaman n * d aynı zamanda pratik bir sayı olmalıdır.
• Tüm pratik sayılar kümesinde ilkel bir pratik sayılar kümesi vardır. İlkel bir pratik sayı ya pratiktir ve karesiz veya pratik ve asal faktörlerinden herhangi birine bölündüğünde çarpanlara ayırma üs 1'den büyükse artık pratik değil. İlkel pratik sayılar dizisi (dizi A267124 içinde OEIS ) başlar

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

Diğer sayı sınıflarıyla ilişkisi

Diğer birkaç önemli tam sayı kümesi yalnızca pratik sayılardan oluşur:

• Yukarıdaki mülklerden n pratik bir sayı ve d bölenlerinden biri (yani, d | n) sonra n * d aynı zamanda pratik bir sayı olmalıdır, bu nedenle 3'ün her kuvvetinin altı katı pratik bir sayı ve 2'nin her kuvvetinin altı katı olmalıdır.
• Her ikinin gücü pratik bir sayıdır.^[6] İkisinin kuvvetleri, pratik sayıların karakterizasyonunu asal çarpanlara ayırmaları açısından önemsiz bir şekilde karşılar: çarpanlara ayırmalarındaki tek asal, p₁, gerektiği gibi ikiye eşittir.
• Her çift mükemmel numara aynı zamanda pratik bir sayıdır.^[6] Bu, Leonhard Euler çift ​​mükemmel bir sayının 2 biçiminde olması gerektiği sonucu^n − 1(2ⁿ - 1). Bu çarpanlara ayırmanın tek olan kısmı, çift parçanın bölenlerinin toplamına eşittir, bu nedenle böyle bir sayının her tek asal çarpanı, en fazla sayının çift parçasının bölenlerinin toplamı olmalıdır. Bu nedenle, bu sayı, pratik sayıların karakterizasyonunu karşılamalıdır.
• Her ilkel (ilkinin ürünü ben bazıları için asal ben) pratiktir.^[6] İlk iki ilkel, iki ve altı için, bu açıktır. Her bir ardışık ilkel, bir asal sayının çarpılmasıyla oluşturulur. p_ben hem ikiye hem de sonraki küçük asal sayıya bölünebilen daha küçük bir ilkel ile, p_ben − 1. Tarafından Bertrand'ın postulatı, p_ben < 2p_ben − 1, bu nedenle ilkseldeki ardışık her asal faktör, bir önceki ilkselin bölenlerinden daha küçüktür. Tümevarım yoluyla, her ilkel, pratik sayıların karakterizasyonunu tatmin eder. Bir ilkel, tanımı gereği karesiz olduğundan, aynı zamanda ilkel bir pratik sayıdır.
• İlkelleri genellemek, ilkinin sıfır olmayan kuvvetlerinin çarpımı olan herhangi bir sayı k asallar da pratik olmalıdır. Bu içerir Ramanujan 's oldukça bileşik sayılar (herhangi bir küçük pozitif tamsayıdan daha fazla bölen olan sayılar) ve faktöryel sayılar.^[6]

Pratik sayılar ve Mısır kesirleri

Eğer n pratik, sonra herhangi rasyonel sayı şeklinde m/n ile m < n toplam olarak temsil edilebilir ∑d_ben/n her biri nerede d_ben farklı bir bölen n. Bu toplamdaki her terim, bir birim kesir, dolayısıyla böyle bir toplam, m/n olarak Mısır kesri. Örneğin,

${ displaystyle { frac {13} {20}} = { frac {10} {20}} + { frac {2} {20}} + { frac {1} {20}} = { frac {1} {2}} + { frac {1} {10}} + { frac {1} {20}}.}$

Fibonacci, 1202 kitabında Liber Abaci^[2] rasyonel bir sayının Mısır kesir temsillerini bulmak için çeşitli yöntemler listeler. Bunlardan ilki, sayının kendisinin zaten bir birim kesir olup olmadığını test etmektir, ancak ikincisi, yukarıda açıklandığı gibi paydanın bölenlerinin toplamı olarak pay temsilini aramaktır. Bu yöntemin yalnızca pratik paydalar için başarılı olacağı garanti edilir. Fibonacci, payda olarak 6, 8, 12, 20, 24, 60 ve 100 pratik sayılara sahip kesirler için bu temsillerin tablolarını sağlar.

Vose (1985) her sayının x/y Mısırlı bir kesir temsiline sahiptir ${ displaystyle scriptstyle O ({ sqrt { log y}})}$ şartlar. Kanıt, bir dizi pratik sayı bulmayı içerir n_ben her sayının şundan küçük olması özelliği ile n_ben toplamı olarak yazılabilir ${ displaystyle scriptstyle O ({ sqrt { log n_ {i-1}}})}$ farklı bölenler n_ben. Sonra, ben öyle seçildi ki n_ben − 1 < y ≤ n_ben, ve xn_ben bölünür y bölüm vermek q ve kalan r. Bu seçimlerden çıkan sonuç ${ displaystyle scriptstyle { frac {x} {y}} = { frac {q} {n_ {i}}} + { frac {r} {yn_ {i}}}}$. Bu formülün sağ tarafındaki her iki payı da bölenlerin toplamlarına genişletmek n_ben istenen Mısır kesir gösterimiyle sonuçlanır. Tenenbaum ve Yokota (1990) farklı bir pratik sayı dizisi içeren benzer bir teknik kullanarak her sayının x/y en büyük paydanın olduğu bir Mısır kesir temsiline sahiptir ${ displaystyle scriptstyle O ({ frac {y log ^ {2} y} { log log y}})}$.

Eylül 2015 varsayımına göre Zhi-Wei Güneş,^[7] her pozitif rasyonel sayı, her paydanın pratik bir sayı olduğu bir Mısır kesir temsiline sahiptir. Varsayımı için bir kanıt var David Eppstein adlı kullanıcının blogu.^[8]

Asal sayılarla analojiler

Pratik sayılara olan ilginin bir nedeni, özelliklerinin çoğunun asal sayılar. Gerçekten de, benzer teoremler Goldbach varsayımı ve ikiz asal varsayım pratik sayılarla bilinir: her pozitif çift tam sayı, iki pratik sayının toplamıdır ve sonsuz sayıda üçlü pratik sayı vardır x − 2, x, x + 2.^[9] Melfi ayrıca sonsuz sayıda pratik olduğunu gösterdi Fibonacci sayıları (sıra A124105 içinde OEIS ); sonsuz sayıda varoluşunun benzer sorusu Fibonacci asalları açık. Hausman ve Shapiro (1984) aralığında her zaman pratik bir sayı olduğunu gösterdi [x²,(x + 1)²] herhangi bir pozitif gerçek için xbenzer bir sonuç Legendre varsayımı asal için. Kısa aralıklarla pratik sayılar üzerindeki bu sonuç, daha sonra kanıtlayan Melfi tarafından geliştirildi. ^[10] Eğer ${ displaystyle s_ {n}}$ pratik sayıların dizisidir, o zaman yeterince büyük n ve uygun bir Bir,

${ displaystyle s_ {n + 1} -s_ {n}$

İzin Vermek p(x) en fazla kaç tane pratik sayı olduğunu sayınx.Margenstern (1991) varsaydı ki p(x) asimptotiktir cx/ logx bazı sabitler için cbenzer bir formül asal sayı teoremi, önceki iddiayı güçlendiriyor Erdős ve Loxton (1979) pratik sayıların tam sayılarda yoğunluğu sıfırdır. Tenenbaum (1986), Saias (1997) bulundu p(x) büyüklük sırasına sahiptir x/ logx.Weingartner (2015) bunu göstererek Margenstern'in varsayımını kanıtladı

${ displaystyle p (x) = { frac {cx} { log x}} sol (1 + O ! sol ({ frac { log log x} { log x}} sağ) sağ),}$

nerede ${ displaystyle c = 1.33607 ...}$^[11] Bu nedenle pratik sayılar, asal sayılardan yaklaşık% 33.6 daha fazla sayıdadır. Sabit faktörün tam değeri ${ displaystyle c}$ tarafından verilir^[12]

${ displaystyle c = { frac {1} {1-e ^ {- gamma}}} sum _ {n { text {pratik}}} { frac {1} {n}} { Biggl (} sum _ {p leq sigma (n) +1} { frac { log p} {p-1}} - log n { Biggr)} prod _ {p leq sigma ( n) +1} left (1 - { frac {1} {p}} sağ),}$

nerede ${ displaystyle gamma}$ ... Euler – Mascheroni sabiti ve ${ displaystyle p}$ asal sayıların üzerinden geçer.

Notlar

Referanslar

• Erdős, Paul; Loxton, J. H. (1979), "Partitio numerorum'daki bazı sorunlar", Avustralya Matematik Derneği Dergisi Seri A, 27 (3): 319–331, doi:10.1017 / S144678870001243X.
• Heyworth, M. R. (1980), "Panaritmik sayılar hakkında daha fazla bilgi", Yeni Zelanda Math. Mag., 17 (1): 24–28. Alıntı yaptığı gibi Margenstern (1991).
• Hausman, Miriam; Shapiro, Harold N. (1984), "Pratik sayılar üzerine", Saf ve Uygulamalı Matematik üzerine İletişim, 37 (5): 705–713, doi:10.1002 / cpa.3160370507, BAY  0752596.
• Margenstern, Maurice (1984), "Résultats et conjectures sur les nombres pratiques", Rendus de l'Académie des Sciences, Série I'den oluşur, 299 (18): 895–898. Alıntı yaptığı gibi Margenstern (1991).
• Margenstern, Maurice (1991), "Les nombres pratiques: théorie, gözlemler ve varsayımlar", Sayılar Teorisi Dergisi, 37 (1): 1–36, doi:10.1016 / S0022-314X (05) 80022-8, BAY  1089787.
• Melfi, Giuseppe (1995), "Pratik sayılar üzerine bir anket", Rend. Sem. Mat. Üniv. Pol. Torino, 53 (4): 347–359.
• Melfi, Giuseppe (1996), "Pratik sayılarla ilgili iki varsayım üzerine", Sayılar Teorisi Dergisi, 56 (1): 205–210, doi:10.1006 / jnth.1996.0012, BAY  1370203.
• Mitrinović, Dragoslav S .; Sandwich, József; Crstici, Borislav (1996), "III.50 Pratik sayılar", Sayı teorisi el kitabı, 1. CiltMatematik ve Uygulamaları, 351, Kluwer Academic Publishers, s. 118–119, ISBN  978-0-7923-3823-9.
• Robinson, D. F. (1979), "Yunan sayı teorisi yoluyla Mısır kesirleri", Yeni Zelanda Math. Mag., 16 (2): 47–52. Alıntı yaptığı gibi Margenstern (1991) ve Mitrinović, indica ve Crstici (1996).
• Saias, Eric (1997), "Diviseurs denses, I", Sayılar Teorisi Dergisi, 62 (1): 163–191, doi:10.1006 / jnth.1997.2057, BAY  1430008.
• Sigler, Laurence E. (çev.) (2002), Fibonacci'den Liber Abaci, Springer-Verlag, s. 119–121, ISBN  0-387-95419-8.
• Sierpiński, Wacław (1955), "Sur une propriété des nombres naturels", Annali di Matematica Pura ed Applicata, 39 (1): 69–74, doi:10.1007 / BF02410762.
• Srinivasan, A. K. (1948), "Pratik sayılar" (PDF), Güncel Bilim, 17: 179–180, BAY  0027799.
• Stewart, B. M. (1954), "Farklı bölenlerin toplamları", Amerikan Matematik Dergisi Johns Hopkins University Press, 76 (4): 779–785, doi:10.2307/2372651, JSTOR  2372651, BAY  0064800.
• Tenenbaum, G. (1986), "Sur un problème de crible et ses uygulamaları", Ann. Sci. Ecole Norm. Sup. (4), 19 (1): 1–30, BAY  0860809.
• Tenenbaum, G.; Yokota, H. (1990), "Mısır fraksiyonlarının uzunluğu ve paydaları", Sayılar Teorisi Dergisi, 35 (2): 150–156, doi:10.1016 / 0022-314X (90) 90109-5, BAY  1057319.
• Vose, M. (1985), "Mısır kesirleri", Londra Matematik Derneği Bülteni, 17 (1): 21, doi:10.1112 / blms / 17.1.21, BAY  0766441.
• Weingartner, A. (2015), "Pratik sayılar ve bölenlerin dağılımı", Üç Aylık Matematik Dergisi, 66 (2): 743–758, arXiv:1405.2585, doi:10.1093 / qmath / hav006.
• Weingartner, A. (2019), "Birkaç ilgili asimptotik tahminde sabit faktör üzerine", Hesaplamanın Matematiği, 88 (318): 1883–1902, arXiv:1705.06349, doi:10.1090 / mcom / 3402.
• Weingartner, A. (2020), "Pratik sayılar için asimptotikteki sabit faktör", Uluslararası Sayı Teorisi Dergisi, 16 (3): 629–638, arXiv:1906.07819, doi:10.1142 / S1793042120500311.

Dış bağlantılar

• Pratik sayı tabloları Giuseppe Melfi tarafından derlendi.
• Pratik Numara -de PlanetMath.
• Weisstein, Eric W. "Pratik Numara". MathWorld.