Ters Gauss dağılımı - Inverse Gaussian distribution

Ters Gauss

Olasılık yoğunluk işlevi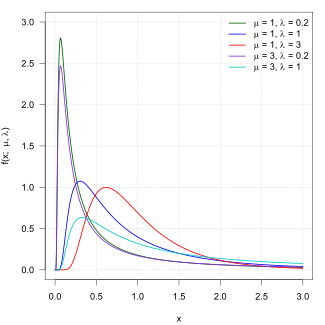
Kümülatif dağılım fonksiyonu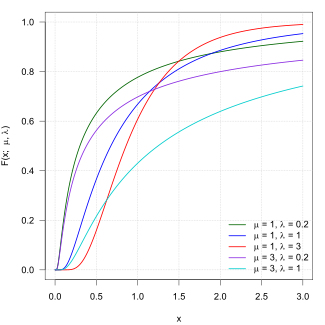
Gösterim	${displaystyle operatorname {IG} left (mu, lambda ight)}$
Parametreler	${displaystyle mu> 0}$ ${displaystyle lambda> 0}$
Destek	${displaystyle xin (0, infty)}$
PDF	${displaystyle {sqrt {frac {lambda} {2pi x ^ {3}}}} exp left [- {frac {lambda (x-mu) ^ {2}} {2mu ^ {2} x}} ight]}$
CDF	${displaystyle Phi sol ({sqrt {frac {lambda} {x}}} sol ({frac {x} {mu}} - 1ight) ight)}$ ${displaystyle {} + exp left ({frac {2lambda} {mu}} ight) Phi sol (- {sqrt {frac {lambda} {x}}} sol ({frac {x} {mu}} + 1ight) ight )}$ nerede ${displaystyle Phi}$ ... standart normal (standart Gauss) dağılımı c.d.f.
Anlamına gelmek	${displaystyle operatorname {E} [X] = mu}$ ${displaystyle operatörü adı {E} [{frac {1} {X}}] = {frac {1} {mu}} + {frac {1} {lambda}}}$
Mod	${displaystyle çok sol [sol (1+ {frac {9mu ^ {2}} {4lambda ^ {2}}} ight) ^ {frac {1} {2}} - {frac {3mu} {2lambda}} ight] }$
Varyans	${displaystyle operatorname {Var} [X] = {frac {mu ^ {3}} {lambda}}}$ ${displaystyle operatorname {Var} [{frac {1} {X}}] = {frac {1} {mu lambda}} + {frac {2} {lambda ^ {2}}}}$
Çarpıklık	${displaystyle 3left ({frac {mu} {lambda}} ight) ^ {1/2}}$
Örn. Basıklık	${displaystyle {frac {15mu} {lambda}}}$
MGF	${displaystyle exp left [{{frac {lambda} {mu}} sol (1- {sqrt {1- {frac {2mu ^ {2} t} {lambda}}}} ight]}$
CF	${displaystyle exp left [{{frac {lambda} {mu}} sol (1- {sqrt {1- {frac {2mu ^ {2} mathrm {i} t} {lambda}}}} ight]}$

İçinde olasılık teorisi, ters Gauss dağılımı (aynı zamanda Wald dağılımı) iki parametreli bir ailedir sürekli olasılık dağılımları ile destek açık (0, ∞).

Onun olasılık yoğunluk fonksiyonu tarafından verilir

${displaystyle f (x; mu, lambda) = {sqrt {frac {lambda} {2pi x ^ {3}}}} exp {iggl (} - {frac {lambda (x-mu) ^ {2}} {2mu ^ {2} x}} {iggr)}}$

için x > 0, nerede ${displaystyle mu> 0}$ ortalama ve ${displaystyle lambda> 0}$ şekil parametresidir.^[1]

Λ sonsuza meylettikçe, ters Gauss dağılımı daha çok bir normal (Gauss) dağılım. Ters Gauss dağılımının bir Gauss dağılımına benzer birkaç özelliği vardır. İsim yanıltıcı olabilir: sadece bunda "ters" dir, Gauss ise Brown hareketi sabit bir zamanda, ters Gauss, pozitif kaymalı bir Brown hareketinin sabit bir pozitif seviyeye ulaşmak için geçen sürenin dağılımını tanımlar.

Kümülant üretme işlevi (karakteristik işlevin logaritması), bir Gauss rasgele değişkeninin kümülant oluşturma işlevinin tersidir.

Belirtmek için bir rastgele değişken X Ortalama μ ve şekil parametresi λ ile ters Gauss dağılımlıdır. ${displaystyle Xsim operatorname {IG} (mu, lambda) ,!}$.

Özellikleri

Tek parametreli form

Ters Gauss dağılımının olasılık yoğunluk fonksiyonu (pdf) aşağıdaki şekilde verilen tek bir parametre formuna sahiptir:

${displaystyle f (x; mu, mu ^ {2}) = {frac {mu} {sqrt {2pi x ^ {3}}}} exp {iggl (} - {frac {(x-mu) ^ {2} } {2x}} {iggr)}.}$

Bu formda dağılımın ortalaması ve varyansı eşittir, ${displaystyle mathbb {E} [X] = {ext {Var}} (X).}$

Ayrıca, tek parametreli ters Gauss dağılımının kümülatif dağılım işlevi (cdf), standart normal dağılımla şu şekilde ilişkilidir:

${displaystyle {egin {hizalı} Pr (X x) & = Phi (-z_ {1}) - e ^ {mu} Phi (z_ {2}), & {ext {for}} & quad xgeq mu .end {hizalı}}}$

nerede ${displaystyle z_ {1} = {frac {mu} {x ^ {1/2}}} - x ^ {1/2}}$ ve ${displaystyle z_ {2} = {frac {mu} {x ^ {1/2}}} + x ^ {1/2},}$ nerede ${displaystyle Phi}$ standart normal dağılımın cdf'sidir. Değişkenler ${displaystyle z_ {1}}$ ve ${displaystyle z_ {2}}$ birbirleriyle kimlikleriyle ilişkilidir ${displaystyle z_ {2} ^ {2} = z_ {1} ^ {2} + 4mu.}$

Tek parametreli formda, MGF şunları basitleştirir:

${displaystyle M (t) = exp [mu (1- {sqrt {1-2t}})].}$

Çift parametreli bir ters Gauss dağılımı ${displaystyle f (x; mu, lambda)}$ tek bir parametreli forma dönüştürülebilir ${displaystyle f (y; mu _ {0}, mu _ {0} ^ {2})}$ uygun ölçeklendirme ile ${displaystyle y = {frac {mu ^ {2} x} {lambda}},}$ nerede ${displaystyle mu _ {0} = mu ^ {3} / lambda.}$

Ters Gauss dağılımının standart biçimi şöyledir:

${displaystyle f (x; 1,1) = {frac {1} {sqrt {2pi x ^ {3}}}} exp {iggl (} - {frac {(x-1) ^ {2}} {2x} } {iggr)}.}$

Özet

Eğer X_ben var ${displaystyle operatorname {IG} (mu _ {0} w_ {i}, lambda _ {0} w_ {i} ^ {2}) ,!}$ dağıtım için ben = 1, 2, ..., nve tüm X_ben vardır bağımsız, sonra

${displaystyle S = sum _ {i = 1} ^ {n} X_ {i} sim operatorname {IG} left (mu _ {0} sum w_ {i}, lambda _ {0} left (sum w_ {i} ight ) ^ {2} ight).}$

Bunu not et

${displaystyle {frac {operatöradı {Var} (X_ {i})} {operatöradı {E} (X_ {i})}} = {frac {mu _ {0} ^ {2} w_ {i} ^ {2} } {lambda _ {0} w_ {i} ^ {2}}} = {frac {mu _ {0} ^ {2}} {lambda _ {0}}}}$

herkes için sabit ben. Bu bir gerekli kondisyon özet için. Aksi takdirde S Ters Gauss dağıtılmayacaktır.

Ölçeklendirme

Herhangi t > 0 bunu tutar

${displaystyle Xsim operatorname {IG} (mu, lambda) ,,,,,, Rightarrow ,,,,,, tXsim operatorname {IG} (tmu, tlambda).}$

Üstel aile

Ters Gauss dağılımı iki parametreli bir üstel aile ile doğal parametreler −λ/(2μ²) ve -λ/ 2 ve doğal istatistikler X ve 1/X.

Brownian hareketi ile ilişki

Bırak Stokastik süreç X_t tarafından verilmek

${displaystyle X_ {0} = 0quad}$

${displaystyle X_ {t} = u t + sigma W_ {t} dörtlü dörtlü dörtlü}$

nerede W_t bir standart Brown hareketi. Yani, X_t kaymalı bir Brown hareketi ${displaystyle u> 0}$.

Sonra ilk geçiş zamanı sabit bir seviye için ${displaystyle alpha> 0}$ tarafından X_t ters Gauss'a göre dağıtılır:

${displaystyle T_ {alpha} = inf {t> 0mid X_ {t} = alpha} sim operatorname {IG} left ({frac {alpha} {u}}, sol ({frac {alpha} {sigma}} ight) ^ {2} ight) = {frac {alpha} {sigma {sqrt {2pi x ^ {3}}}}} exp {iggl (} - {frac {(alpha -ux) ^ {2}} {2sigma ^ {2 } x}} {iggr)}}$

(çapraz başvuru Schrödinger^[2] denklem 19, Smoluchowski^[3], denklem 8 ve Folks^[4], denklem 1).

Sürüklenme sıfır olduğunda

Brown hareketinde kayma olmadığında yukarıdakilerin ortak bir özel durumu ortaya çıkar. Bu durumda parametre μ sonsuza meyillidir ve sabit seviye için ilk geçiş zamanı α olasılık yoğunluk işlevine sahiptir

${displaystyle fleft (x; 0, left ({frac {alpha} {sigma}} ight) ^ {2} ight) = {frac {alpha} {sigma {sqrt {2pi x ^ {3}}}} exp left (- {frac {alpha ^ {2}} {2sigma ^ {2} x}} sağ)}$

(ayrıca bkz Bachelier^[5]:74[6]:39). Bu bir Lévy dağılımı parametrelerle ${displaystyle c = left ({frac {alpha} {sigma}} ight) ^ {2}}$ ve ${displaystyle mu = 0}$.

Maksimum olasılık

Model nerede

${displaystyle X_ {i} sim operatorname {IG} (mu, lambda w_ {i}) ,,,,,,, i = 1,2, ldots, n}$

hepsiyle w_ben bilinen, (μ, λ) bilinmeyen ve tümü X_ben bağımsız aşağıdaki olasılık işlevine sahiptir

${displaystyle L (mu, lambda) = sol ({frac {lambda} {2pi}} sağ) ^ {frac {n} {2}} sol (prod _ {i = 1} ^ {n} {frac {w_ { i}} {X_ {i} ^ {3}}} ight) ^ {frac {1} {2}} exp left ({frac {lambda} {mu}} toplam _ {i = 1} ^ {n} w_ {i} - {frac {lambda} {2mu ^ {2}}} toplam _ {i = 1} ^ {n} w_ {i} X_ {i} - {frac {lambda} {2}} toplam _ {i = 1} ^ {n} w_ {i} {frac {1} {X_ {i}}} ight).}$

Olasılık denklemini çözmek, aşağıdaki maksimum olasılık tahminlerini verir

${displaystyle {widehat {mu}} = {frac {toplam _ {i = 1} ^ {n} w_ {i} X_ {i}} {toplam _ {i = 1} ^ {n} w_ {i}}} ,,,,,,,,, {frac {1} {widehat {lambda}}} = {frac {1} {n}} toplam _ {i = 1} ^ {n} w_ {i} sol ({frac {1} {X_ {i}}} - {frac {1} {widehat {mu}}} ight).}$

${displaystyle {widehat {mu}}}$ ve ${displaystyle {widehat {lambda}}}$ bağımsızdır ve

${displaystyle {widehat {mu}} sim operatorname {IG} left (mu, lambda sum _ {i = 1} ^ {n} w_ {i} ight), qquad {frac {n} {widehat {lambda}}} sim {frac {1} {lambda}} chi _ {n-1} ^ {2}.}$

Ters Gauss dağılımından örnekleme

Aşağıdaki algoritma kullanılabilir.^[7]

Ortalama 0 ve standart sapma 1'e eşit olan normal bir dağılımdan rastgele bir varyasyon oluşturun

${displaystyle displaystyle u sim N (0,1).}$

Değerin karesini al

${ekran stili görüntü stili y = u ^ {2}}$

ve ilişkiyi kullan

${displaystyle x = mu + {frac {mu ^ {2} y} {2lambda}} - {frac {mu} {2lambda}} {sqrt {4mu lambda y + mu ^ {2} y ^ {2}}}. }$

Başka bir rastgele varyasyon oluşturun, bu sefer 0 ile 1 arasındaki tekdüze bir dağılımdan örneklenir

${displaystyle displaystyle zsim U (0,1).}$

Eğer${displaystyle zleq {frac {mu} {mu + x}}}$sonra geri dön${displaystyle displaystyle x}$yoksa geri dön${displaystyle {frac {mu ^ {2}} {x}}.}$

İçindeki örnek kod Java:

halka açık çift ters Gauss(çift mu, çift lambda) {    Rastgele rand = yeni Rastgele();    çift v = rand.sonrakiGauss();  // Ortalama 0 ve 1 standart sapma ile normal dağılımdan örnek    çift y = v * v;    çift x = mu + (mu * mu * y) / (2 * lambda) - (mu / (2 * lambda)) * Matematik.sqrt(4 * mu * lambda * y + mu * mu * y * y);    çift Ölçek = rand.nextDouble();  // 0 ile 1 arasındaki tek tip dağılımdan örnek    Eğer (Ölçek <= (mu) / (mu + x))        dönüş x;    Başka        dönüş (mu * mu) / x;}

Python kullanarak matplotlib ve NumPy yardımıyla Wald dağıtımı

Ve Wald dağılımını çizmek için Python kullanma matplotlib ve Dizi:

ithalat matplotlib.pyplot gibi pltithalat dizi gibi nph = plt.geçmiş(np.rastgele.Wald(3, 2, 100000), çöp kutuları=200, yoğunluk=Doğru)plt.göstermek()

İlgili dağılımlar

• Eğer ${displaystyle Xsim operatorname {IG} (mu, lambda)}$, sonra ${displaystyle kXsim operatorname {IG} (kmu, klambda)}$ herhangi bir numara için ${displaystyle k> 0.}$^[1]
• Eğer ${displaystyle X_ {i} sim operatörü adı {IG} (mu, lambda),}$ sonra ${displaystyle toplamı _ {i = 1} ^ {n} X_ {i} sim operatörü adı {IG} (nmu, n ^ {2} lambda),}$
• Eğer ${displaystyle X_ {i} sim operatörü adı {IG} (mu, lambda),}$ için ${displaystyle i = 1, ldots, n,}$ sonra ${displaystyle {ar {X}} sim operatörü adı {IG} (mu, nlambda),}$
• Eğer ${displaystyle X_ {i} sim operatör adı {IG} (mu _ {i}, 2mu _ {i} ^ {2}),}$ sonra ${displaystyle toplam _ {i = 1} ^ {n} X_ {i} sim operatörü adı {IG} sol (toplam _ {i = 1} ^ {n} mu _ {i}, 2left (toplam _ {i = 1} ^ {n} mu _ {i} ight) ^ {2} ight),}$
• Eğer ${displaystyle Xsim operatorname {IG} (mu, lambda)}$, sonra ${displaystyle lambda (X-mu) ^ {2} / mu ^ {2} Xsim chi ^ {2} (1)}$.^[8]

Ters bir Gauss dağılımının (bir Wald dağılımı) ve bir üstel (bir eski Wald dağılımı) evrişimi, psikolojide tepki süreleri için bir model olarak kullanılır,^[9] bir örnek olarak görsel arama ile.^[10]

Tarih

Bu dağılım ilk olarak 1900'de, Louis Bachelier^[5][6] bir hisse senedinin ilk kez belirli bir fiyata ulaştığı anda. 1915'te bağımsız olarak Erwin Schrödinger^[2] ve Marian / Smoluchowski^[3] Brown hareketinin ilk geçiş zamanı olarak. Üreme modellemesi alanında, Hadwiger işlevi olarak bilinir. Hugo Hadwiger 1940'ta tanımlayan.^[11] Abraham Wald bu dağılım 1944'te yeniden türetildi^[12] sıralı olasılık oranı testinde bir numunenin sınırlayıcı formu olarak. Ters Gauss ismini öneren Maurice Tweedie 1945'te.^[13] Tweedie bu dağılımı 1956'da araştırdı^[14] ve 1957^[15][16] ve bazı istatistiksel özelliklerini oluşturdu. Dağıtım, 1978'de Folks ve Chhikara tarafından kapsamlı bir şekilde gözden geçirildi.^[4]

Sayısal hesaplama ve yazılım

Olasılık yoğunluk fonksiyonu için basit formüle rağmen, ters Gauss dağılımı için sayısal olasılık hesaplamaları yine de tüm parametre değerleri için kayan nokta aritmetiğinde tam makine doğruluğu elde etmek için özel dikkat gerektirir.^[17] Ters Gauss dağılımı için fonksiyonlar, R programlama dili rmutil dahil çeşitli paketler tarafından,^[18][19] SuppDists,^[20] STAR,^[21] invGauss,^[22] LaplacesDemon,^[23] ve statmod.^[24]

Ayrıca bakınız

• Genelleştirilmiş ters Gauss dağılımı
• Tweedie dağılımları Ters Gauss dağılımı, Tweedie ailesinin bir üyesidir üstel dağılım modelleri
• Durma zamanı

Referanslar

daha fazla okuma

• Høyland, Arnljot; Rausand, Marvin (1994). Sistem Güvenilirliği Teorisi. New York: Wiley. ISBN  978-0-471-59397-3.
• Seshadri, V. (1993). Ters Gauss Dağılımı. Oxford University Press. ISBN  978-0-19-852243-0.

Dış bağlantılar

• Ters Gauss Dağılımı Wolfram web sitesinde.